| ID | dad age | mom race | informal support | city ID | city name | enforce intensity | benefit level | city ind. 1 | city ind. 2 | city ind. 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 19 | hisp | 1 | 1 | Oakland | 0.52 | 1.01 | 1 | 0 | 0 |
| 2 | 27 | black | 0 | 1 | Oakland | 0.52 | 1.01 | 1 | 0 | 0 |
| 3 | 26 | black | 1 | 1 | Oakland | 0.52 | 1.01 | 1 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 248 | 19 | white | 1 | 3 | Baltimore | 0.05 | 1.1 | 0 | 0 | 0 |
| 249 | 26 | black | 1 | 3 | Baltimore | 0.05 | 1.1 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 1366 | 21 | black | 1 | 20 | Norfolk | -0.11 | 1.08 | 0 | 0 | 1 |
| 1367 | 28 | hisp | 0 | 20 | Norfolk | -0.11 | 1.08 | 0 | 0 | 1 |
1 Estructuras Multinivel
1.1 Definición General
- Extensión de regresión donde los datos están estructurados en grupos.
- Los coeficientes pueden variar por grupo.
- Aplicaciones: datos agrupados, mediciones repetidas, series de tiempo seccionales, estructuras no anidadas.
- Ejemplo inicial: personas dentro de ciudades, con información a nivel persona y ciudad.
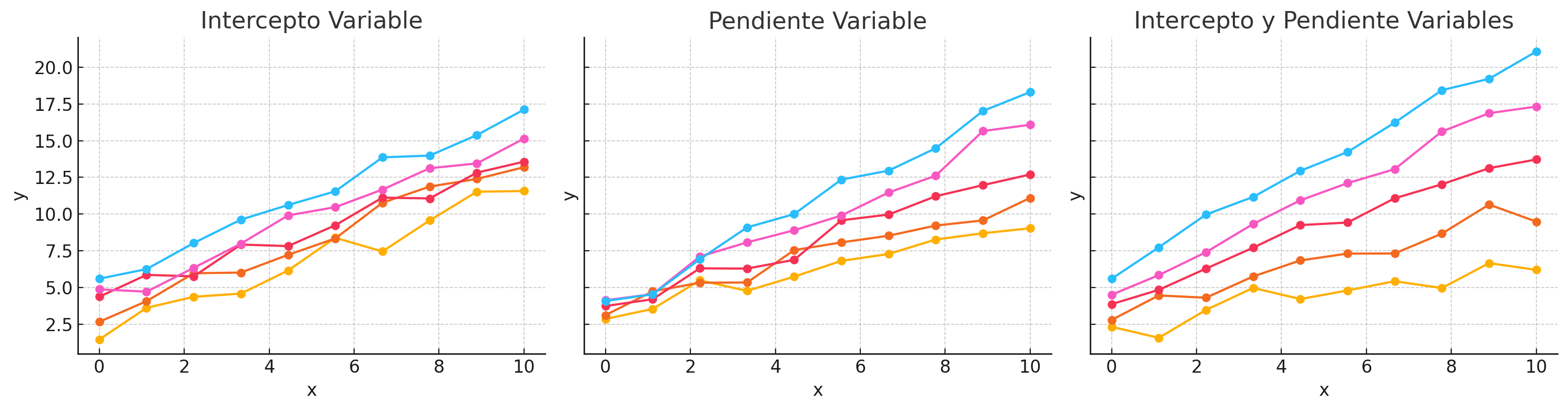
1.2 Modelos de Intercepto y Pendiente Variables
1.2.1 Modelo de Intercepto Variable
- Regresión con indicadores de grupo → cada grupo tiene su propio intercepto.
- Fórmula:
\[ y_i = \alpha_{j[i]} + \beta x_i + \epsilon_i \]
- \(j[i]\): índice del grupo al que pertenece la observación \(i\).
- \(x_i\): predictor continuo.
- Interpretación: diferencia en el nivel base de \(y\) entre grupos.
1.2.2 Modelo de Pendiente Variable
- Intercepto constante pero pendiente distinta por grupo.
- Fórmula:
\[ y_i = \alpha + \beta_{j[i]} x_i + \epsilon_i \]
- \(x\) interactúa con la pertenencia al grupo.
- Útil cuando el efecto de \(x\) sobre \(y\) cambia por grupo.
1.2.3 Modelo de Intercepto y Pendiente Variables
- Tanto intercepto como pendiente varían por grupo.
- Fórmula:
\[ y_i = \alpha_{j[i]} + \beta_{j[i]} x_i + \epsilon_i \]
- Representa una interacción completa entre \(x\) y el grupo.
Estimación:
Estimar todos los \(\alpha_j\) y \(\beta_j\) puede ser difícil, especialmente si hay predictores a nivel de grupo.
Procedimiento típico:
- Paso 1: Ajustar una regresión con coeficientes variables.
- Paso 2: Modelar esos coeficientes como función de variables a nivel de grupo.
1.2.4 Sintaxis en R (lme4)
library(lme4)
# Ejemplo: personas (y) dentro de ciudades (group), predictor x
# Modelo de intercepto variable
modelo_int_var <- lmer(y ~ x + (1 | group), data = datos)
# Modelo de pendiente variable
modelo_slope_var <- lmer(y ~ 1 + (x | group), data = datos)
# Modelo de intercepto y pendiente variables
modelo_int_slope_var <- lmer(y ~ (x | group), data = datos)
# Resumen de resultados
summary(modelo_int_var)
summary(modelo_slope_var)
summary(modelo_int_slope_var)Notas sobre el código:
(1 | group)→ intercepto aleatorio por grupo.(x | group)→ intercepto y pendiente aleatorios.lmer()del paquete lme4 es estándar para estos modelos.
1.3 Datos Clusterizados
1.3.1 Estructura Multinivel de los Datos
Estructura Clásica: un vector \(y\) y una matriz \(X\) de predictores.
Estructura Multinivel: cada nivel (individual, grupo) tiene su propia matriz de predictores.
Ejemplo: Efecto de políticas de enforcement en el pago de manutención infantil por padres no casados.
- Tratamiento: intensidad de enforcement → nivel ciudad.
- Outcome: apoyo informal recibido → nivel individuo.
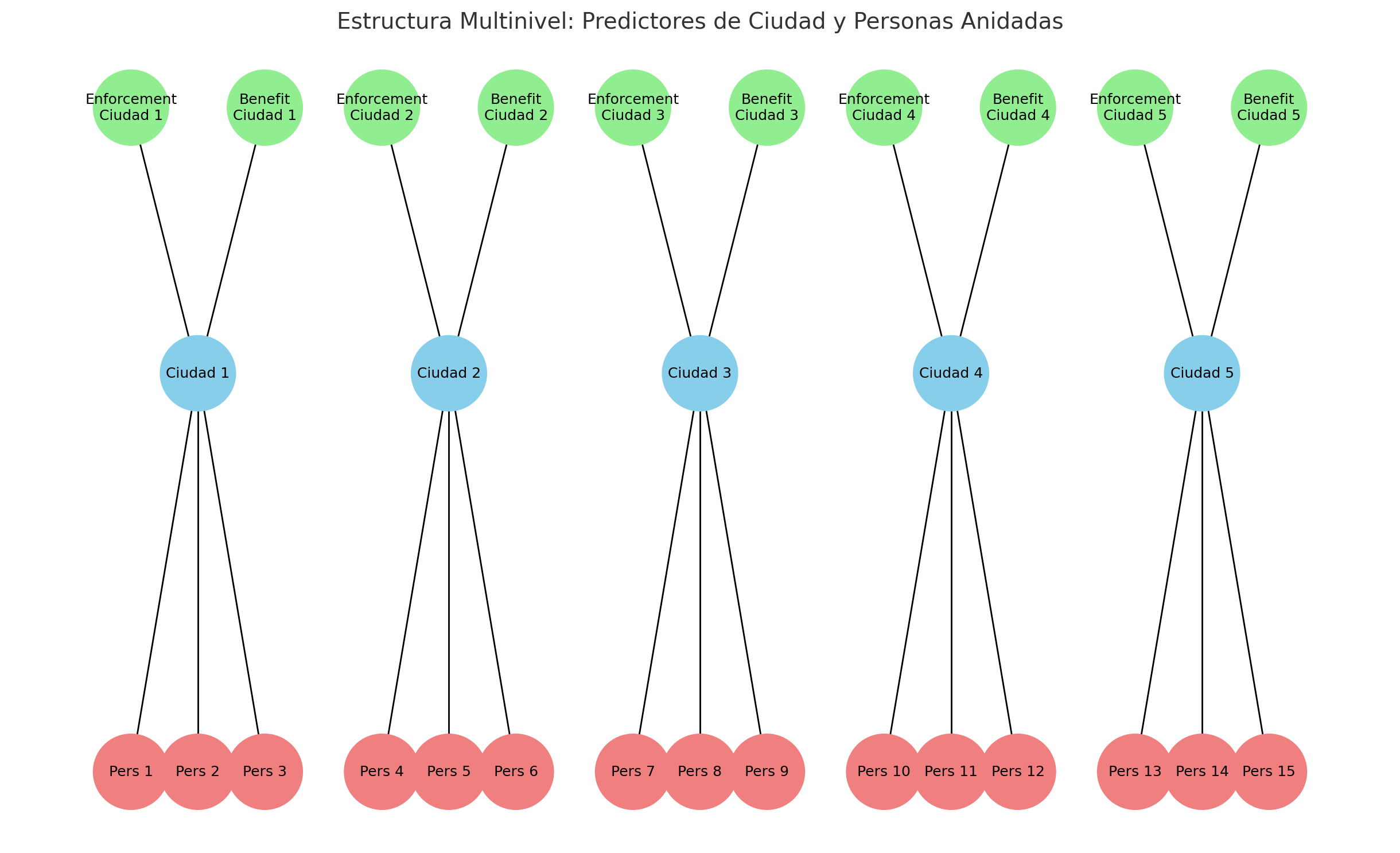
1.3.2 Organización de Datos
1.3.2.1 Formato de una sola matriz
- Una fila por persona.
- Variables de nivel ciudad repetidas para cada individuo.
1.3.2.2 Formato de dos matrices
Matriz individual: variables como edad del padre, raza de la madre, apoyo informal,
city_id.Matriz ciudad: nombre ciudad, enforcement, nivel de beneficios.
Ventajas:
- Cada información se guarda una sola vez → menos errores.
- Claridad en qué variables son de nivel individual y cuáles de nivel ciudad.
| ID | dad age | mom race | informal support | city ID |
|---|---|---|---|---|
| 1 | 19 | hisp | 1 | 1 |
| 2 | 27 | black | 0 | 1 |
| 3 | 26 | black | 1 | 1 |
| … | … | … | … | … |
| 248 | 19 | white | 1 | 3 |
| 249 | 26 | black | 1 | 3 |
| … | … | … | … | … |
| 1366 | 21 | black | 1 | 20 |
| 1367 | 28 | hisp | 0 | 20 |
| city ID | city name | enforcement | benefit level |
|---|---|---|---|
| 1 | Oakland | 0.52 | 1.01 |
| 2 | Austin | 0 | 0.75 |
| 3 | Baltimore | -0.05 | 1.1 |
| … | … | … | … |
| 20 | Norfolk | -0.11 | 1.08 |
1.3.3 Métodos de Análisis
1.3.3.1 Regresión a Nivel Individual
- Modelo:
\[ \Pr(y_i = 1) = \operatorname{logit}^{-1}(X_i \beta) \]
\(X\) incluye:
- Constante.
- Intensidad de enforcement (nivel ciudad).
- Edad padre, raza madre (nivel individual).
- Nivel de beneficios (nivel ciudad).
Problema: ignora variación entre ciudades no explicada por estos predictores.
1.3.3.2 Regresión a Nivel Ciudad
- Promediar variables individuales por ciudad.
- \(y_j\): media de apoyo informal en ciudad \(j\).
- Ventaja: errores automáticamente a nivel ciudad.
- Desventaja: pierde variabilidad individual.
| city ID | city name | enforcement | benefit level | # in sample | avg. age | prop. black | proportion with informal support |
|---|---|---|---|---|---|---|---|
| 1 | Oakland | 0.52 | 1.01 | 78 | 25.9 | 0.67 | 0.55 |
| 2 | Austin | 0 | 0.75 | 91 | 25.8 | 0.42 | 0.54 |
| 3 | Baltimore | -0.05 | 1.1 | 101 | 27 | 0.86 | 0.67 |
| … | … | … | … | … | … | … | … |
| 20 | Norfolk | -0.11 | 1.08 | 31 | 27.4 | 0.84 | 0.65 |
1.3.4 Análisis en Dos Pasos
Este enfoque separa explícitamente el análisis en dos niveles (individual y grupo), pero los ajusta de manera secuencial en lugar de simultánea como en un modelo multinivel.
Paso 1: Regresión logística a nivel individual
- Objetivo: Estimar la probabilidad de que el individuo \(i\) reciba apoyo informal (\(y_i = 1\)), usando predictores de nivel individual y dummies para cada ciudad.
- Modelo:
\[ \Pr(y_i = 1) = \text{logit}^{-1} \left( \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \delta_{j[i]} \right) \]
donde:
- \(x_{i1}, \dots, x_{ip}\) → predictores de nivel individual (edad padre, raza madre, etc.).
- \(\delta_{j[i]}\) → efecto fijo para la ciudad \(j\) a la que pertenece el individuo \(i\) (dummy de ciudad).
- Se incluyen todas las ciudades como indicadores para capturar diferencias no explicadas por los predictores individuales.
Resultado del paso 1: Obtenemos estimaciones \(\hat{\delta}_1, \dots, \hat{\delta}_J\), que representan el efecto promedio de cada ciudad sobre el resultado, controlando por variables individuales.
Paso 2: Regresión a nivel ciudad
- Objetivo: Explicar la variación entre ciudades usando predictores agregados a nivel ciudad.
- Modelo:
\[ \hat{\delta}_j = \gamma_0 + \gamma_1 z_{j1} + \cdots + \gamma_q z_{jq} + \eta_j \]
donde:
- \(z_{j1}, \dots, z_{jq}\) → predictores de nivel ciudad (ej. intensidad de enforcement, nivel de beneficios).
- \(\eta_j\) → error a nivel ciudad.
Interpretación: Se busca entender qué características de las ciudades explican por qué algunas tienen mayor probabilidad promedio de apoyo informal que otras, después de controlar por características individuales.
Ventajas
- Claridad conceptual: separa efectos individuales y efectos de ciudad.
- Simplicidad computacional: se ajustan dos modelos estándar (logístico y lineal).
- Permite examinar explícitamente los \(\hat{\delta}_j\) como “scores” de ciudad.
Problemas y Limitaciones
Muestras pequeñas por grupo
- Si algunas ciudades tienen pocos casos, las estimaciones \(\hat{\delta}_j\) serán inestables y tendrán alta varianza.
- Esto puede distorsionar la regresión del paso 2.
Interacciones individuo–grupo
- Si el efecto de un predictor individual (p.ej. edad padre) varía entre ciudades, el método de dos pasos no captura esta interacción de forma directa.
- Ejemplo: enforcement puede ser más efectivo en ciudades con padres mayores, pero el modelo de dos pasos no integra estos términos cruzados simultáneamente.
Pérdida de eficiencia
- Ajustar por separado ignora la incertidumbre conjunta de los dos niveles.
- En un modelo multinivel, ambos niveles se estiman de forma simultánea, aprovechando toda la información y produciendo mejores estimaciones.
1.3.5 Modelo Multinivel
Formulación
- Nivel individual (logístico):
\[ \Pr(y_i = 1) = \operatorname{logit}^{-1}(X_i \beta + \alpha_{j[i]}), \quad i=1,\dots,n \]
- Nivel ciudad (regresión para interceptos):
\[ \alpha_j \sim N(U_j \gamma, \sigma_\alpha^2), \quad j=1,\dots,20 \]
- \(X\): predictores individuales.
- \(U\): predictores de ciudad.
- \(\sigma_\alpha\): desviación estándar de efectos no explicados a nivel ciudad.
Ventajas
- Incluye todos los interceptos de ciudad sin colinealidad.
- Estima \(\sigma_\alpha\) junto con \(\alpha\), \(\beta\), \(\gamma\).
1.4 Medidas repetidas
Un caso típico de datos multinivel son las medidas repetidas sobre los mismos individuos.
Aquí, las observaciones están anidadas dentro de las personas, y se pueden incluir predictores tanto en el nivel de la medición como en el nivel de la persona.
library(tidyverse)
library(arm)
library(readr)1.4.1 Ejemplo: adolescentes australianos
- Conjunto longitudinal de ≈ 2000 adolescentes.
- Se registraron sus patrones de consumo de tabaco cada seis meses, durante 3 años.
Carga de datos:
smoking <- read_delim('../ARM_Data/smoking/smoke_pub.dat') Rows: 8730 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: "\t"
dbl (5): newid, sex(1=F), parsmk, wave, smkreg
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.smoking <- smoking %>%
rename(sex = `sex(1=F)`) %>%
mutate(sex = factor(sex))Exploración inicial: prevalencia del fumado
Podemos graficar la prevalencia de fumado por ola y sexo:
prevalencia <- smoking %>%
group_by(sex, wave) %>%
summarise(prevalencia = mean(smkreg)) `summarise()` has grouped output by 'sex'. You can override using the `.groups`
argument.ggplot() +
geom_line(data = prevalencia, aes(x = wave, y = prevalencia, color = sex)) +
theme_minimal() +
labs(title = 'Prevalencia de fumado por sexo',
x = 'Aplicación del cuestionario',
y = 'Prevalencia de fumado')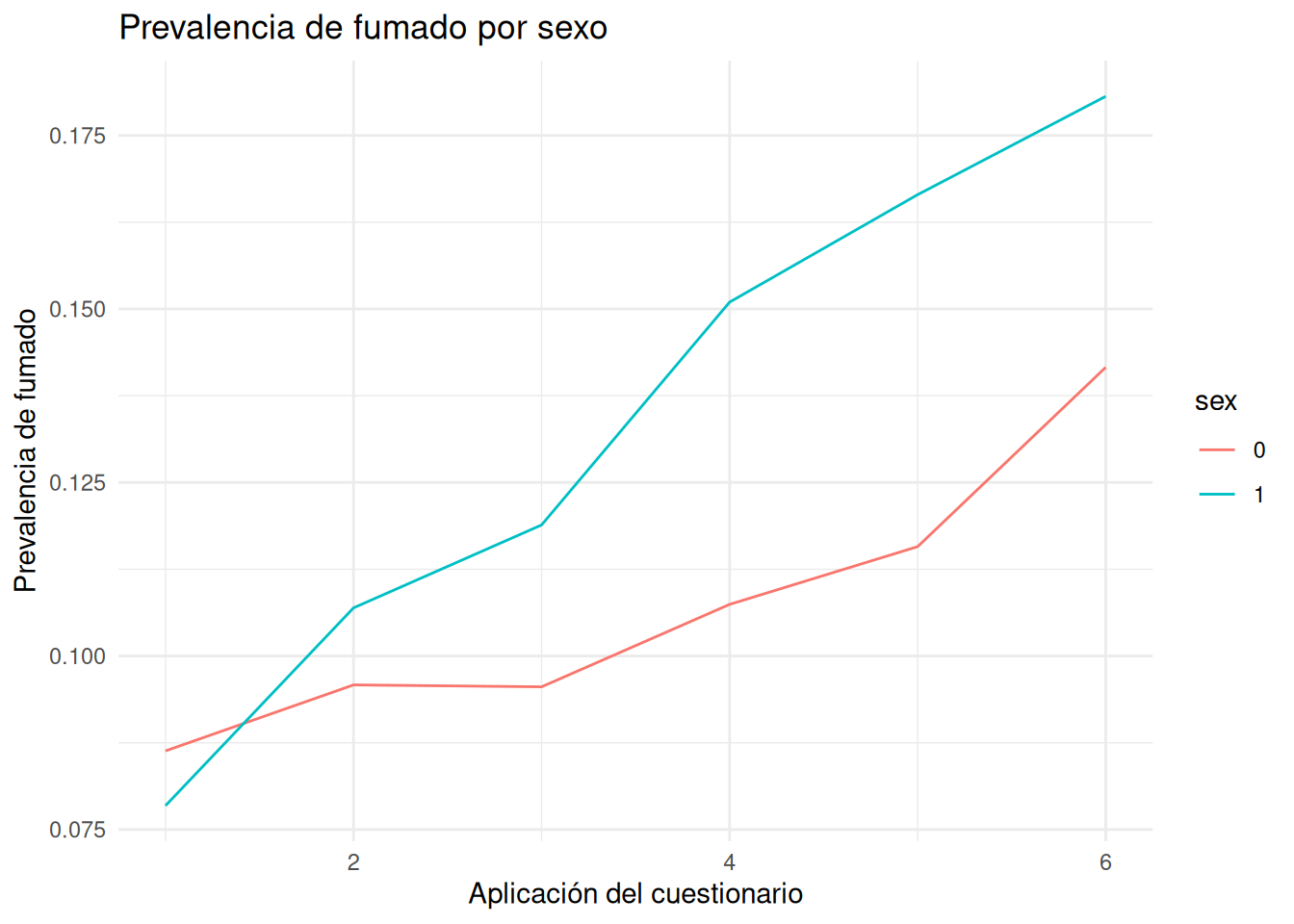
Separación de niveles de análisis
Podemos organizar los datos en dos matrices, siguiendo el enfoque multinivel:
Nivel 1 (observaciones, waves)
smoking_ind <- smoking %>%
dplyr::select(wave, newid, smkreg) %>%
arrange(wave, newid)
head(smoking_ind)# A tibble: 6 × 3
wave newid smkreg
<dbl> <dbl> <dbl>
1 1 1 0
2 1 2 0
3 1 3 0
4 1 4 0
5 1 5 0
6 1 6 0Nivel 2 (personas)
smoking_group <- smoking %>%
dplyr::select(newid, sex, parsmk) %>%
distinct()
head(smoking_group)# A tibble: 6 × 3
newid sex parsmk
<dbl> <fct> <dbl>
1 1 1 0
2 2 0 0
3 3 1 0
4 4 1 0
5 5 0 0
6 6 0 01.4.2 Modelo multinivel
1.4.2.1 Formulación con índice doble
Para persona \(j\) en ola \(t\):
\[ \Pr(y_{jt}=1) = \operatorname{logit}^{-1}\Big( \beta_{0} + \beta_{1} \, \text{psmoke}_{j} + \beta_{2} \, \text{female}_{j} + \beta_{3}(1-\text{female}_{j}) \cdot t + \beta_{4}\,\text{female}_{j} \cdot t + \alpha_{j} \Big) \]
1.4.3 Formulación con índice único
Con observación \(i\), persona \(j[i]\) y ola \(t[i]\):
\[ \Pr(y_{i}=1) = \operatorname{logit}^{-1}\Big( \beta_{0} + \beta_{1}\,\text{psmoke}_{j[i]} + \beta_{2}\,\text{female}_{j[i]} + \beta_{3}(1-\text{female}_{j[i]})\cdot t[i] + \beta_{4}\,\text{female}_{j[i]}\cdot t[i] + \alpha_{j[i]} \Big) \]
Equivalencia y elección de tipo de modelo
- Ambos modelos son equivalentes.
- Primer formato: conveniente cuando todos los individuos tienen mediciones regulares.
- Segundo formato: preferible en estructuras irregulares (diferente número de mediciones por persona).
1.5 Datos de series de tiempo con corte transversal
En contextos donde las tendencias temporales globales son importantes, los datos de medidas repetidas se denominan a veces time-series cross-sectional (TSCS).
1.5.1 Ejemplo:
- Estudio sobre la proporción de veredictos de pena de muerte revertidos en cada uno de 34 estados de USA durante 23 años (1973–1995).
- Datos en nivel estado × año.
- Interés: estudiar la variación entre estados y a lo largo del tiempo.
1.5.2 Características de los TSCS:
- Suelen tener estructura rectangular: observaciones en intervalos de tiempo regulares.
- A diferencia de mediciones repetidas generales, que pueden ser irregulares (ej.: en el estudio de adolescentes fumadores algunos niños podrían ser medidos una sola vez, otros mensualmente o anualmente).
- Comúnmente presentan patrones de tiempo globales (ej.: expansión de la pena de muerte entre 1970s y 1990s).
- En este marco, los datos estado-año deben considerarse como anidados dentro de estados y también dentro de años, con predictores potenciales en los tres niveles.
- Estos modelos se discuten más a fondo en la Sección 13.5.
1.6 Otras estructuras no anidadas
1.6.1 Definición
Los datos no anidados aparecen cuando los individuos están caracterizados por categorías superpuestas de atributos.
1.6.2 Ejemplo: ingresos
Un estudio sobre ingresos considerando ocupación y estado de residencia:
- Encuesta con ≈ 1500 personas.
- 40 categorías ocupacionales.
- 50 estados.
Modelo de regresión: Se predice el log-ingreso con predictores individuales \(X\), dummies de ocupación y estado:
\[ y_{i}=X_{i} \beta+\alpha_{j[i]}+\gamma_{k[i]}+\epsilon_{i}, \quad i=1, \ldots, n \]
- \(j[i]\): categoría ocupacional de la persona \(i\).
- \(k[i]\): estado de residencia de la persona \(i\).
Este modelo se vuelve multinivel al incluir regresiones para los coeficientes de ocupación y estado.
Ecuaciones multinivel
Ocupación \[ \alpha_{j} \sim N(U_{j}a, \, \sigma_{\alpha}^{2}), \quad j=1, \ldots, 40 \]
- \(U\): matriz de predictores a nivel ocupación (ej.: estatus social, indicador de supervisión).
- \(a\): vector de coeficientes del modelo de ocupación.
- \(\sigma_{\alpha}\): desviación estándar de los errores a nivel ocupación.
Estado \[ \gamma_{k} \sim N(V_{k}g, \, \sigma_{\gamma}^{2}), \quad k=1, \ldots, 50 \]
- \(V\): matriz de predictores a nivel estado.
- \(g\): vector de coeficientes del modelo de estado.
- \(\sigma_{\gamma}\): desviación estándar de los errores a nivel estado.
Naturaleza no anidada del modelo
El modelo anterior es no anidado porque: - Las categorías ocupacionales \(j[i]\) no son subconjuntos de los estados \(k[i]\),
- Ni los estados \(k[i]\) son subconjuntos de las ocupaciones \(j[i]\).
Limitación
La notación de regresión se vuelve engorrosa en modelos multinivel complejos por la necesidad de introducir símbolos adicionales (\(U, V, a, g\), etc.) que representan:
- matrices de datos,
- coeficientes,
- errores en distintos niveles.
1.7 Variables indicadoras y efectos fijos o aleatorios
1.7.1 Regresión clásica: baseline y \(J-1\) indicadores
En regresión clásica, al incluir una variable categórica con \(J\) categorías:
- Se elige una categoría como baseline.
- Se incluyen \(J-1\) variables indicadoras.
Ejemplo: Con \(J=20\) ciudades en el estudio de pensión alimenticia, se toma la ciudad 1 (Oakland) como baseline e indicadores para las otras 19. El coeficiente de cada ciudad refleja la comparación con Oakland.
Regresión Multinivel: inclusión de todos los \(J\) indicadores
En un modelo multinivel no es necesario elegir un baseline. Se incluyen los \(J\) indicadores (por ejemplo, las 20 ciudades del estudio).
- En regresión clásica, esto generaría colinealidad con la constante.
- En un modelo multinivel, los coeficientes de grupo se modelan por una distribución de nivel superior, eliminando el problema de colinealidad.
1.7.2 Efectos fijos y aleatorios
En modelos multinivel:
- Los coeficientes que varían (\(\alpha_j\), \(\beta_j\)) se llaman a veces efectos aleatorios: son realizaciones de un modelo probabilístico de nivel superior.
- Efectos fijos: coeficientes que varían pero no se modelan probabilísticamente.
Ejemplo: regresión clásica con \(J-1=19\) indicadores de ciudad puede llamarse “modelo de efectos fijos”.
Problema: la literatura presenta definiciones contradictorias.
1.7.3 Cinco definiciones observadas:
Kreft y De Leeuw (1998): efectos fijos son constantes entre individuos, efectos aleatorios varían.
- Ejemplo: modelo de crecimiento \(y_{it}=\alpha_i+\beta t\), con interceptos aleatorios y pendiente fija.
Searle, Casella y McCulloch (1992): efectos fijos si son de interés en sí mismos, aleatorios si interesa la población subyacente.
Green y Tukey (1960): si la muestra agota la población → efecto fijo; si es una parte pequeña → efecto aleatorio.
LaMotte (1983): si un efecto se considera el valor realizado de una v.a. aleatoria → efecto aleatorio.
Snijders y Bosker (1999); econometría: efectos fijos se estiman por MCO o ML; efectos aleatorios con shrinkage (predicción lineal insesgada).
- En multinivel: efectos fijos \(\beta_j\) se estiman condicional a \(\sigma_\beta = \infty\), efectos aleatorios con \(\sigma_\beta\) estimado de los datos.
Consecuencias:
- Un mismo factor puede ser “fijo” según una definición y “aleatorio” según otra.
- La confusión es amplia y no hay respuestas claras (Searle et al., 1992).
Recomendación de los autores:
- Evitar los términos “fijo” y “aleatorio”.
- Describir directamente el modelo (ej.: interceptos que varían, pendientes constantes).
- Usar siempre modelado multinivel.
1.8 Costos y beneficios del modelado multinivel
1.8.1 Revisión rápida de la regresión clásica
Antes de profundizar en el modelado multinivel, se recuerda que con la regresión clásica es posible:
- Hacer predicción para variables continuas o discretas,
- Ajustar relaciones no lineales mediante transformaciones,
- Incluir predictores categóricos usando variables indicadoras,
- Modelar interacciones entre predictores,
- Realizar inferencia causal (bajo condiciones apropiadas).
1.8.2 Motivaciones para el modelado multinivel
Existen varias razones para preferir un modelo multinivel, ya sea para inferencia causal, estudio de variación o predicción:
Considerar la variación individual y grupal al estimar coeficientes a nivel de grupo.
- Ejemplo: en el estudio de pensión alimenticia, interesa un predictor a nivel de ciudad, pero en regresión clásica no es posible incluir indicadores de ciudad y predictores de ciudad simultáneamente.
Modelar variación entre coeficientes individuales.
- En regresión clásica esto puede hacerse con variables indicadoras, pero el modelo multinivel facilita describir la variación entre grupos, predecir para grupos nuevos y capturar la incertidumbre grupal.
Estimar coeficientes para grupos específicos.
- Ejemplo: estimación de niveles de radón en condados de Minnesota. El modelo multinivel permite obtener estimaciones razonables incluso en condados con muestras pequeñas, lo cual resulta difícil con regresión clásica.
1.8.3 Complejidad de los modelos multinivel
- Una desventaja potencial es la complejidad adicional al permitir que coeficientes varíen por grupo.
- Esta complejidad refleja mayor realismo, pero genera dificultades de interpretación y resumen.
1.8.4 Supuestos adicionales del modelado multinivel
Un modelo multinivel requiere supuestos adicionales más allá de la regresión clásica. Cada nivel corresponde a su propia regresión con supuestos como:
- Aditividad,
- Linealidad,
- Independencia,
- Homocedasticidad,
- Normalidad.
Relación con regresión clásica:
La regresión clásica puede verse como caso especial del modelo multinivel:
- Pooling completo (varianza jerárquica = 0),
- Pooling nulo (varianza jerárquica = ∞).
Justificación práctica: los supuestos adicionales permiten modelos más realistas y útiles en la práctica.
1.8.5 ¿Cuándo marca la diferencia el modelado multinivel?
Comparación entre enfoques:
- Poca variación grupal: el modelo multinivel se reduce a regresión clásica sin indicadores de grupo.
- Mucha variación grupal: el modelo multinivel se reduce a regresión clásica con indicadores de grupo.
- Número pequeño de grupos (< 5): no hay suficiente información para estimar variación grupal; los beneficios del multinivel son limitados.
Conclusión
- El mayor beneficio ocurre en situaciones intermedias, donde la variación grupal es apreciable pero no extrema.
- No hay gran riesgo en aplicar un modelo multinivel, siempre que se acepte el esfuerzo adicional para especificar el modelo e interpretar los resultados.