# Mini-ejemplo en R: Cuadrado latino 5x5 (millet) y modelo multinivel
# ---------------------------------------------------------------
# Carga de paquetes
library(tidyverse)
library(lme4)
library(broom.mixed)
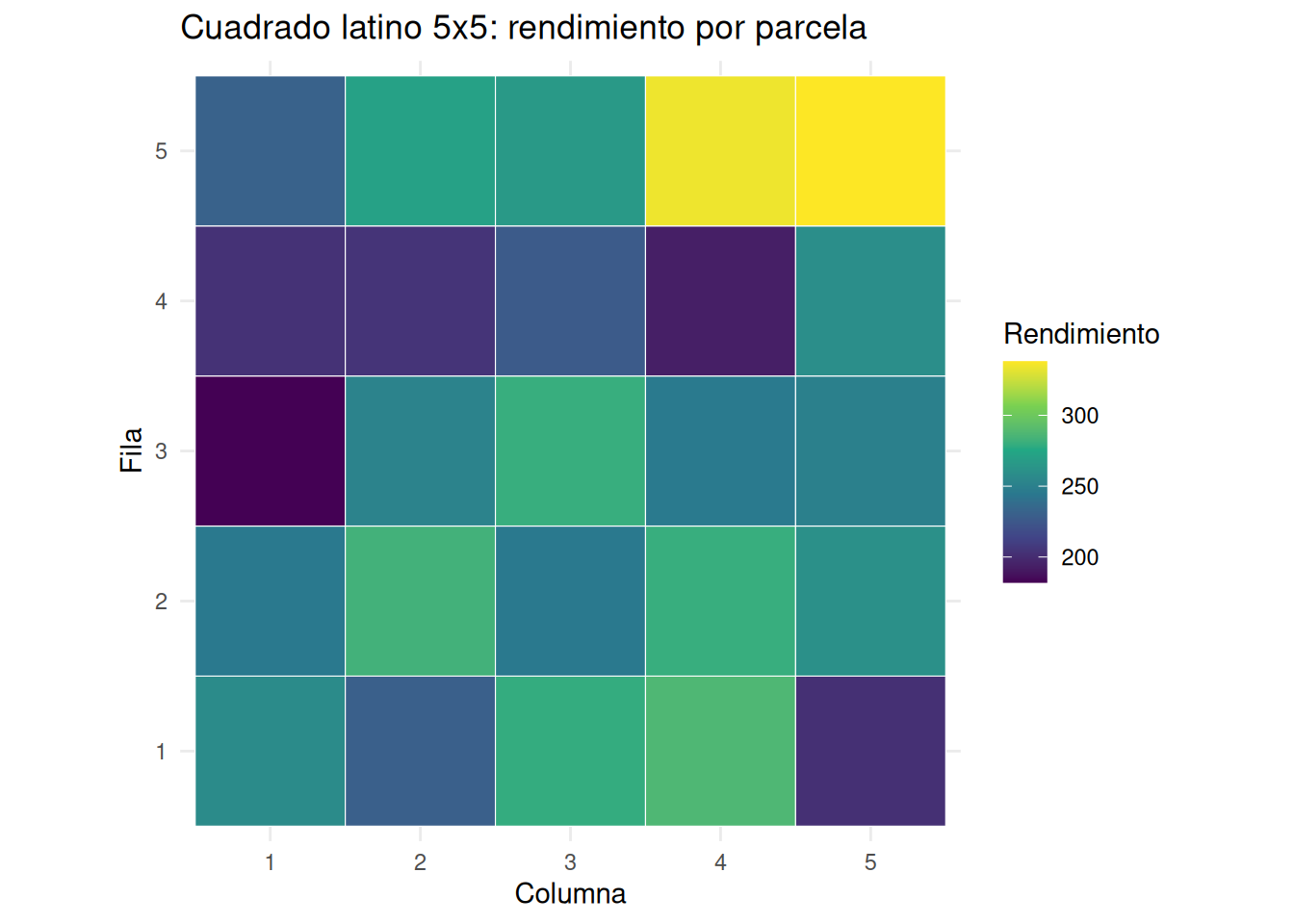
# 1) Ingresar los datos (tabla de la Figura 13.11)
# Cada celda: Tratamiento (A–E) y rendimiento (yield)
latin_raw <- tribble(
~row, ~col, ~treat, ~yield,
1, 1, "B", 257,
1, 2, "E", 230,
1, 3, "A", 279,
1, 4, "C", 287,
1, 5, "D", 202,
2, 1, "D", 245,
2, 2, "A", 283,
2, 3, "E", 245,
2, 4, "B", 280,
2, 5, "C", 260,
3, 1, "E", 182,
3, 2, "B", 252,
3, 3, "C", 280,
3, 4, "D", 246,
3, 5, "A", 250,
4, 1, "A", 203,
4, 2, "C", 204,
4, 3, "D", 227,
4, 4, "E", 193,
4, 5, "B", 259,
5, 1, "C", 231,
5, 2, "D", 271,
5, 3, "B", 266,
5, 4, "A", 334,
5, 5, "E", 338
)
latin <- latin_raw %>%
mutate(
row = factor(row),
col = factor(col),
treat = factor(treat, levels = c("A","B","C","D","E")),
# Predictores lineales (centrados) para tendencias por fila/columna/tratamiento
row_c = as.integer(row) - 3,
col_c = as.integer(col) - 3,
trt_c = as.integer(treat) - 3
)
# 2) Exploración rápida
latin %>%
summarise(
n = n(),
mean_yield = mean(yield),
sd_yield = sd(yield)
)