5  Modelos lineales generalizados multinivel (GLMMs)

Este capítulo presenta modelos lineales generalizados multinivel (GLMMs), análogos a las regresiones lineal y logística, pero extendidos a respuestas no gaussianas mediante enlaces y distribuciones de la familia exponencial. La idea central es incluir indicadores de grupo y modelos a nivel de grupo para capturar variación estructurada. Se ilustran tres aplicaciones: (i) un modelo Poisson sobredisperso para detenciones policiales, (ii) un multinomial logístico para storable voting, y (iii) otro Poisson sobredisperso para redes sociales.

5.1 Regresión Poisson sobredispersa: detenciones policiales y etnicidad

Contexto (NYC): se comparan grupos étnicos controlando por variación a nivel de precinto (75 en total) (unidades de área). Se permiten efectos por precinto (consistentes con teorías de política policial local como “broken windows”) y se estratifica por composición étnica del vecindario: <10% población negra; 10–40%; >40%. Se hacen análisis separados por estrato.

5.1.1 Sobredispersión como componente de varianza

Un GLM tiene sobredispersión si la varianza de los datos excede la predicha por el modelo. En Poisson/ Binomial no hay parámetro de varianza libre, por lo que se introduce variabilidad adicional con un componente de varianza a nivel de dato:

  • Modelo Poisson clásico:

    \[ y_i \sim \text{Poisson}\!\left(u_i\,e^{X_i\beta}\right). \]

  • Poisson sobredisperso multinivel:

    \[ \begin{aligned} y_i &\sim \text{Poisson}\!\left(u_i\,e^{X_i\beta+\epsilon_i}\right),\\ \epsilon_i &\sim \mathrm{N}\!\left(0,\sigma_\epsilon^2\right). \end{aligned} \]

El hiperparámetro \(\sigma_\epsilon\) cuantifica la sobredispersión; si \(\sigma_\epsilon=0\), se recupera el Poisson clásico.

5.1.2 Modelo Poisson multinivel con offset

Para cada grupo étnico \(e=1,2,3\) y precinto \(p\), se modela el número de detenciones \(y_{ep}\) con indicadores étnicos, efectos de precinto y offset basado en arrestos del año previo (\(n_{ep}\)), escalados a 15 meses (\(\frac{15}{12}\)):

\[ \begin{aligned} y_{ep} &\sim \text{Poisson}\!\left(\frac{15}{12}\,n_{ep}\,e^{\mu+\alpha_e+\beta_p+\epsilon_{ep}}\right),\\ \alpha_e &\sim \mathrm{N}(0,\sigma_\alpha^2),\\ \beta_p &\sim \mathrm{N}(0,\sigma_\beta^2),\\ \epsilon_{ep} &\sim \mathrm{N}(0,\sigma_\epsilon^2). \end{aligned} \]

  • \(\alpha_e\): efecto por etnia; \(\beta_p\): efecto por precinto; \(\epsilon_{ep}\): sobredispersión.
  • \(\sigma_\beta\): variación entre precintos; \(\sigma_\epsilon\): variación extra no explicada por Poisson.

Objetivo del bloque: Generar un conjunto de datos sintético que siga el modelo (15.1), con tres grupos étnicos (\(e=1,2,3\)), \(P=60\) precintos y sobredispersión a nivel observación. Usaremos como baseline (offset) el log de los arrestos del año previo escalados a 15 meses.

set.seed(5454)  # para reproducibilidad
# Parámetros "verdaderos" de la simulación
E  <- 3                    # etnias
P  <- 60                   # precintos
mu <- -1.0                 # intercepto en la escala log
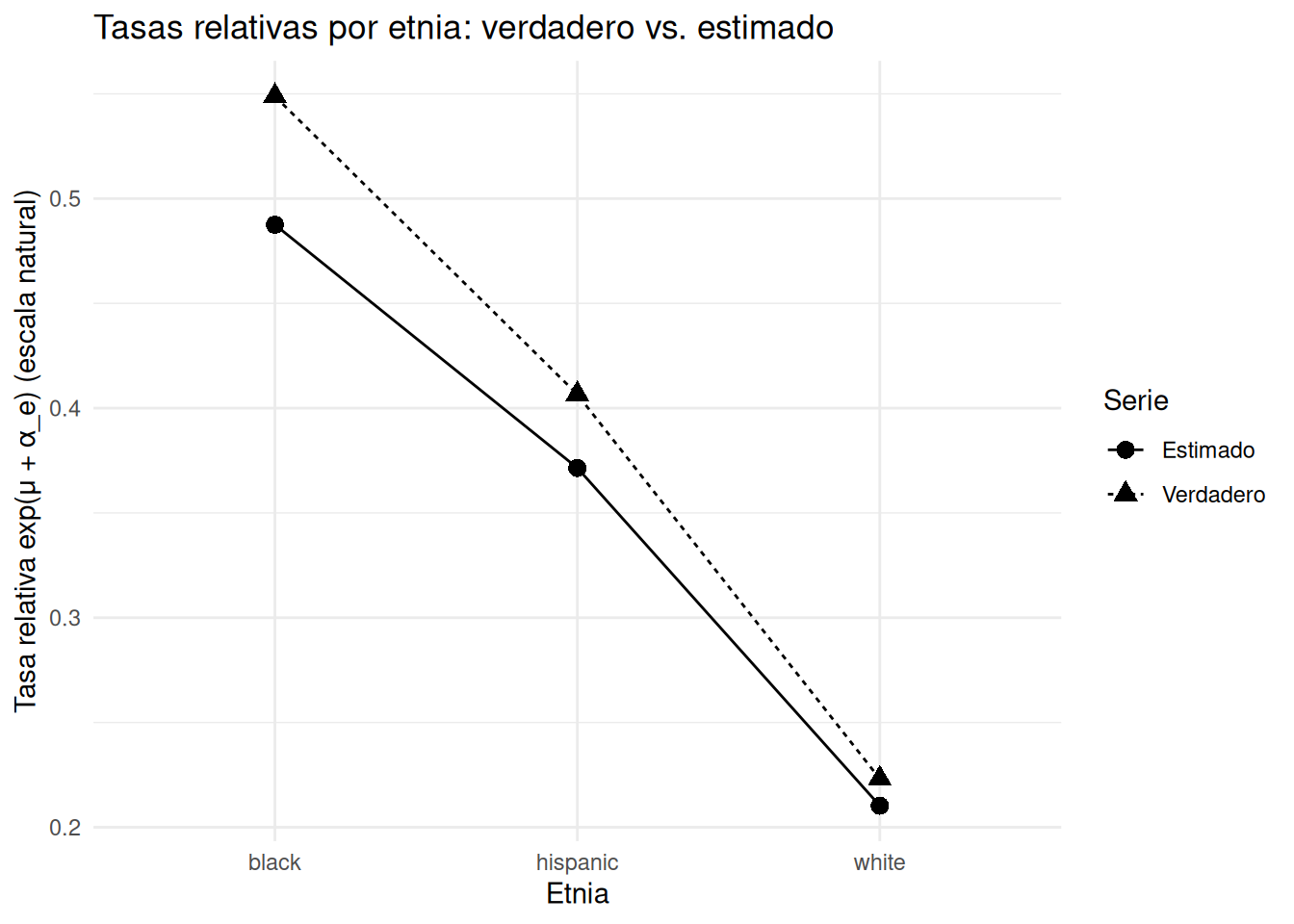
alpha_true <- c( 0.40, 0.10, -0.50 ) # efectos por etnia: blacks, hispanics, whites (suma != 0, luego centraremos)
sigma_beta     <- 0.50     # sd entre precintos
sigma_epsilon  <- 0.30     # sd de sobredispersión (log-escala)
lambda_arresto <- 50       # media base de arrestos por celda (antes de escalado)
scale_15m      <- 15/12    # factor de 15 meses

# Diseño completo (todas las combinaciones etnia-precinto)
design <- expand_grid(
  eth = factor(1:E, labels = c("black","hispanic","white")),
  precinct = factor(1:P)
) %>%
  # Asignamos un ID único por observación (para OLRE)
  mutate(obs_id = row_number())

# Efectos aleatorios por precinto
beta_precinct <- rnorm(P, mean = 0, sd = sigma_beta)
names(beta_precinct) <- levels(design$precinct)

# Sobredispersión a nivel observación (OLRE, normal en la escala log)
eps_obs <- rnorm(nrow(design), mean = 0, sd = sigma_epsilon)

# Arrestos del año previo: n_ep ~ Poisson(lambda_arresto) (no negativos)
n_prev <- rpois(nrow(design), lambda = lambda_arresto) %>% pmax(1)

# Tasa esperada de "stops" (en escala log) siguiendo (15.1):
# log E[y_ep] = log( (15/12) * n_ep ) + mu + alpha_e + beta_p + eps_ep
linpred <- log(scale_15m * n_prev) +
           mu +
           alpha_true[as.integer(design$eth)] +
           beta_precinct[as.character(design$precinct)] +
           eps_obs

# Respuesta: y_ep ~ Poisson( exp(linpred) )
y <- rpois(nrow(design), lambda = exp(linpred))

# Armamos el data frame final
sim_data <- design %>%
  mutate(
    n_prev = n_prev,
    y      = y
  )

glimpse(sim_data)
Rows: 180
Columns: 5
$ eth      <fct> black, black, black, black, black, black, black, black, black…
$ precinct <fct> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
$ obs_id   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
$ n_prev   <dbl> 54, 45, 46, 38, 45, 56, 50, 39, 42, 49, 56, 51, 46, 48, 55, 5…
$ y        <int> 80, 37, 48, 87, 43, 39, 24, 23, 6, 23, 45, 23, 53, 27, 46, 10…

Objetivo del bloque: Ajustar un GLMM Poisson con offset \(\log\left(\tfrac{15}{12}n_{ep}\right)\), efectos aleatorios por etnia \((1|\text{eth})\), por precinto \((1|\text{precinct})\) y un efecto aleatorio a nivel de observación \((1|\text{obs\_id})\) para capturar la sobredispersión (OLRE):

# Offset en log: log( (15/12) * n_prev )
sim_data <- sim_data %>%
  mutate(offset_log = log(scale_15m * n_prev))

# Ajuste con lme4::glmer (Poisson) y OLRE
# Nota: (1|obs_id) introduce varianza extra a nivel de dato (sobredispersión).
fit <- glmer(
  y ~ 1 + (1|eth) + (1|precinct) + (1|obs_id),
  family = poisson(link = "log"),
  offset = offset_log,
  data   = sim_data,
  control = glmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e5))
)

summary(fit)
Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: poisson  ( log )
Formula: y ~ 1 + (1 | eth) + (1 | precinct) + (1 | obs_id)
   Data: sim_data
 Offset: offset_log
Control: glmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+05))

      AIC       BIC    logLik -2*log(L)  df.resid 
   1363.8    1376.6    -677.9    1355.8       176 

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-1.70891 -0.41107 -0.01976  0.33736  1.01406 

Random effects:
 Groups   Name        Variance Std.Dev.
 obs_id   (Intercept) 0.07009  0.2647  
 precinct (Intercept) 0.24735  0.4973  
 eth      (Intercept) 0.13082  0.3617  
Number of obs: 180, groups:  obs_id, 180; precinct, 60; eth, 3

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.1054     0.2201  -5.022 5.11e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

5.1.2.1 Reparametrización con suma-cero en un lote

Para comparar grupos étnicos, se trabaja con coeficientes centrados:

\[ \alpha_e^{\text{adj}}=\alpha_e-\bar{\alpha},\quad e=1,2,3, \]

y se ajusta el intercepto:

\[ \mu^{\text{adj}}=\mu+\bar{\alpha}. \]

Así, \(\mu^{\text{adj}}+\alpha_e^{\text{adj}}=\mu+\alpha_e\) para cada \(e\), sin cambiar el modelo para los datos. Se recomienda ajustar el modelo completo y luego derivar estos parámetros restringidos.

Objetivo del bloque: Extraer \(\mu\) y los efectos por etnia, centrar \(\alpha_e\) a suma-cero y calcular \(e^{\mu^{\text{adj}}+\alpha^{\text{adj}}_e}\) para interpretar tasas relativas de “stops” (ajustado por precinto y baseline de arrestos).

# Intercepto estimado (fijo)
mu_hat <- fixef(fit)[["(Intercept)"]]

# Efectos aleatorios por etnia (BLUPs): ranef(fit)$eth es un data.frame con columna `(Intercept)`
re_eth <- ranef(fit)$eth %>%
  tibble::rownames_to_column("eth") %>%
  rename(alpha_hat = `(Intercept)`)

# Centramos a suma-cero: alpha_adj = alpha_hat - mean(alpha_hat)
alpha_bar   <- mean(re_eth$alpha_hat)
re_eth <- re_eth %>%
  mutate(alpha_adj = alpha_hat - alpha_bar)

# Ajustamos el intercepto: mu_adj = mu_hat + alpha_bar
mu_adj <- mu_hat + alpha_bar

# Tasas relativas por etnia: exp(mu_adj + alpha_adj),
# que son comparables con exp(mu + alpha_true) del DGP.
results_eth <- re_eth %>%
  mutate(
    rate_rel_est = exp(mu_adj + alpha_adj)
  ) %>%
  # Unimos con "verdaderos" para comparar
  left_join(
    tibble(
      eth = c("black","hispanic","white"),
      alpha_true = alpha_true
    ),
    by = "eth"
  ) %>%
  mutate(rate_rel_true = exp(mu + alpha_true))

results_eth
       eth  alpha_hat   alpha_adj rate_rel_est alpha_true rate_rel_true
1    black  0.3869886  0.37092541    0.4875245        0.4     0.5488116
2 hispanic  0.1150766  0.09901342    0.3714553        0.1     0.4065697
3    white -0.4538756 -0.46993883    0.2102876       -0.5     0.2231302

Objetivo del bloque: Graficar las tasas relativas verdaderas y estimadas por etnia para evaluar la recuperación del modelo y la claridad de interpretación.

plot_df <- results_eth %>%
  select(eth, rate_rel_true, rate_rel_est) %>%
  pivot_longer(cols = starts_with("rate_rel"),
               names_to = "type", values_to = "value") %>%
  mutate(type = recode(type,
                       rate_rel_true = "Verdadero",
                       rate_rel_est  = "Estimado"))

ggplot(plot_df, aes(x = eth, y = value, shape = type, linetype = type, group = type)) +
  geom_point(size = 3) +
  geom_line() +
  labs(
    title = "Tasas relativas por etnia: verdadero vs. estimado",
    x = "Etnia",
    y = "Tasa relativa exp(μ + α_e) (escala natural)",
    shape = "Serie",
    linetype = "Serie"
  ) +
  theme_minimal()

5.1.3 Especificaciones alternativas del modelo

Se evalúa la sensibilidad a: (a) diferentes particiones de precintos y (b) el rol de \(n_{ep}\) (arrestos previos).

5.1.3.1 Variabilidad entre precintos: predictores a nivel de precinto

En lugar de agrupar precintos, se incluyen predictores de composición étnica del precinto (proporción negra \(z_{1p}\) e hispana \(z_{2p}\)):

\[ y_{ep}\sim \text{Poisson}\!\left(\frac{15}{12}\,n_{ep}\,e^{\mu+\alpha_e+\zeta_1 z_{1p}+\zeta_2 z_{2p}+\beta_p+\epsilon_{ep}}\right). \]

Las inferencias sobre \(\alpha_e^{\text{adj}}\) son similares a las del análisis por estratos. Incluir términos cuadráticos e interacción (\(z_{1p}^2\), \(z_{2p}^2\), \(z_{1p}z_{2p}\)) no altera los hallazgos principales.

5.1.3.2 Usar \(\log n_{ep}\) como predictor en lugar de offset

Alternativa:

\[ y_{ep}\sim \text{Poisson}\!\left(\frac{15}{12}\,e^{\gamma\log n_{ep}+\mu+\alpha_e+\beta_p+\epsilon_{ep}}\right), \]

que se reduce a (15.1) si \(\gamma=1\). Al estimar \(\gamma\), se obtiene \(\gamma\approx 1\), y los \(\alpha_e^{\text{adj}}\) quedan esencialmente iguales; varía el intercepto por centrado de \(\log n_{ep}\).

5.2 Regresión multinomial ordenada y no ordenada: votos almacenables

En esta sección se estudia la regresión multinomial, la cual extiende los modelos logísticos y probit a variables categóricas con más de dos niveles. Estas categorías pueden ser ordenadas (por ejemplo, Sí/No/Tal vez, o niveles de frecuencia) o no ordenadas (por ejemplo, partidos políticos, deportes, medios de transporte). Se presentan tanto la formulación matemática de los modelos para categorías ordenadas como ejemplos prácticos de su aplicación.

5.2.1 Resultados categóricos ordenados y no ordenados

Se distinguen dos tipos de resultados:

  • Ordenados: categorías con un orden natural (ejemplo: Demócrata, Independiente, Republicano; Siempre, Frecuentemente, A veces, Nunca).
  • No ordenados: categorías sin un orden intrínseco (ejemplo: Fútbol, Baloncesto, Béisbol, Hockey).

5.2.2 El modelo logit multinomial ordenado

Para un resultado categórico \(y \in {1,2,\ldots,K}\), el modelo logístico ordenado se expresa como una secuencia de regresiones logísticas:

\[ \begin{align*} \Pr(y > 1) &= \operatorname{logit}^{-1}(X\beta) \\ \Pr(y > 2) &= \operatorname{logit}^{-1}(X\beta - c_{2}) \\ \Pr(y > 3) &= \operatorname{logit}^{-1}(X\beta - c_{3}) \\ &\vdots \\ \Pr(y > K-1) &= \operatorname{logit}^{-1}(X\beta - c_{K-1}) \end{align*} \]

donde los parámetros de corte \(c_{k}\) (o umbrales) cumplen \(0 = c_{1} < c_{2} < \cdots < c_{K-1}\).

De esta forma, la probabilidad de un resultado específico se obtiene como:

\[ \Pr(y = k) = \operatorname{logit}^{-1}(X\beta - c_{k-1}) - \operatorname{logit}^{-1}(X\beta - c_{k}). \]

5.2.3 Interpretación con variable latente y puntos de corte

El modelo ordenado se puede interpretar mediante una variable latente \(z\):

\[ y_i = \begin{cases} 1 & \text{si } z_i < 0 \\ 2 & \text{si } z_i \in (0, c_2) \\ 3 & \text{si } z_i \in (c_2, c_3) \\ ;\vdots & \\ K & \text{si } z_i > c_{K-1} \end{cases} \]

con \(z_i = X_i \beta + \epsilon_i\), donde los errores \(\epsilon_i\) siguen una distribución logística.

5.2.4 Ejemplo: votos almacenables

Ilustramos el análisis de datos categóricos ordenados con un estudio de economía experimental sobre el tema de los “votos almacenables” (storable votes). Este ejemplo es relativamente complejo y muestra tanto la utilidad como las posibles limitaciones del modelo logístico ordenado.

En el experimento, se reclutó a estudiantes universitarios para participar en una serie de juegos de votación. En cada juego, un conjunto de \(k\) jugadores debía votar sobre dos temas. La particularidad era que cada jugador recibía un total de 4 votos para distribuir. En el primer tema, el jugador podía elegir asignar 1, 2 o 3 votos; los votos restantes se destinaban automáticamente al segundo tema. El lado ganador en cada tema se decidía por mayoría simple, y los jugadores del lado ganador recibían una recompensa positiva, sorteada de una distribución uniforme en el intervalo \([1,100]\).

Para maximizar su ganancia esperada, los jugadores debían adoptar una estrategia: asignar más votos a aquellos temas con mayor potencial de beneficio. La mecánica experimental era la siguiente: antes de cada votación, se informaba a los jugadores la distribución de las posibles recompensas, así como su pago potencial para el primer tema. Con esa información decidían cuántos votos asignar (1, 2 o 3). Luego se revelaba el pago potencial del segundo tema, pero en este caso no había decisión estratégica, pues los votos sobrantes se transferían automáticamente.

De esta manera, las estrategias de los jugadores podían resumirse en su elección inicial \(y \in {1,2,3}\), condicionada al pago potencial \(x\) del primer tema.

No fue sorprendente observar que las respuestas eran en general monótonas: los estudiantes tendían a gastar más votos cuando el beneficio potencial era mayor. Sin embargo, resultó interesante constatar la diversidad de estrategias “aproximadamente monótonas” que se adoptaron.

Tal como se aprecia en la Figura 6.4 del libro, el comportamiento de la mayoría de los individuos puede resumirse mediante tres parámetros clave:

  1. El punto de corte entre asignar 1 y 2 votos.
  2. El punto de corte entre asignar 2 y 3 votos.
  3. El grado de “difuminación” o incertidumbre en estas divisiones.

Los dos primeros parámetros caracterizan la estrategia monótona elegida, mientras que la nitidez de las divisiones refleja la consistencia con que dicha estrategia se aplicó.

El modelo ordenado captura cómo el número de votos iniciales depende del beneficio potencial:

\[ y_i = \begin{cases} 1 & \text{si } z_i < c_{1.5} \\ 2 & \text{si } z_i \in (c_{1.5}, c_{2.5}) \\ 3 & \text{si } z_i > c_{2.5} \end{cases}, \] \[\quad z_i \sim \text{logística}(x_i, \sigma^2).\]

Aquí, \(c_{1.5}\) y \(c_{2.5}\) son puntos de corte en la escala de beneficios \(x\), y \(\sigma\) mide la suavidad de la transición entre categorías.

5.2.4.1 Diferentes parametrizaciones equivalentes

Existen varias formas equivalentes del modelo:

  1. Con puntos de corte definidos directamente (\(c_{1.5}, c_{2.5}\)).
  2. Con intercepto y pendiente: \(z_i = \alpha + \beta x + \epsilon_i\).
  3. Con pendiente pero sin intercepto: \(z_i = \beta x + \epsilon_i\).

Estas parametrizaciones son equivalentes mediante transformaciones algebraicas, pero la primera es la más interpretativa.

5.2.5 Ajuste del modelo en R

Objetivo del bloque

Simular un conjunto de datos ordinales (3 categorías) a partir de \(x\sim U(0,100)\) con umbrales verdaderos conocidos \((c_{1.5},c_{2.5},\sigma)\) y generar \(y\in{1,2,3}\).

set.seed(123)

# Parámetros "verdaderos" para la simulación
c15_true <- 25    # umbral entre 1 y 2 (en escala de x)
c25_true <- 55    # umbral entre 2 y 3 (en escala de x)
sigma_true <- 12  # difuminación de los cortes

# Función logística inversa
invlogit <- function(x) exp(x)/(1+exp(x))

# Simulación de covariable y probabilidades ordinales
n <- 600
datos_sim <- tibble(
  x = runif(n, 0, 100)
) |>
  mutate(
    p1 = 1 - invlogit((x - c15_true)/sigma_true),
    p3 = invlogit((x - c25_true)/sigma_true),
    p2 = 1 - p1 - p3,
    # Muestreo de y = 1,2,3 con probabilidades (p1,p2,p3)
    y = pmap_int(list(p1, p2, p3), ~ sample(1:3, size = 1, prob = c(..1, ..2, ..3)))
  )

datos_sim
# A tibble: 600 × 5
       x      p1     p3     p2     y
   <dbl>   <dbl>  <dbl>  <dbl> <int>
 1 28.8  0.422   0.101  0.477      2
 2 78.8  0.0111  0.879  0.110      3
 3 40.9  0.210   0.236  0.554      2
 4 88.3  0.00509 0.941  0.0536     3
 5 94.0  0.00316 0.963  0.0340     3
 6  4.56 0.846   0.0147 0.139      1
 7 52.8  0.0897  0.455  0.456      2
 8 89.2  0.00471 0.945  0.0498     3
 9 55.1  0.0750  0.503  0.422      3
10 45.7  0.152   0.315  0.534      2
# ℹ 590 more rows

Objetivo del bloque

Ajustar un modelo logit ordenado con MASS::polr() y resumir resultados.

library(MASS)

Attaching package: 'MASS'
The following object is masked from 'package:dplyr':

    select
# Ajuste (forma de odds proporcionales, método logístico)
fit_polr <- polr(factor(y) ~ x, data = datos_sim, method = "logistic", Hess = TRUE)

# Resumen amigable
summary(fit_polr)
Call:
polr(formula = factor(y) ~ x, data = datos_sim, Hess = TRUE, 
    method = "logistic")

Coefficients:
    Value Std. Error t value
x 0.09359   0.005609   16.68

Intercepts:
    Value   Std. Error t value
1|2  2.3524  0.2144    10.9714
2|3  5.2205  0.3202    16.3047

Residual Deviance: 749.9276 
AIC: 755.9276

Objetivo del bloque

Transformar la salida estándar \((\hat\beta, \hat\theta_{1|2}, \hat\theta_{2|3})\) a la parametrización de cortes sobre la escala de x: \[ \hat c_{1.5}=\frac{\hat\theta_{1|2}}{\hat\beta},\quad \hat c_{2.5}=\frac{\hat\theta_{2|3}}{\hat\beta},\quad \hat\sigma=\frac{1}{\hat\beta}. \]

# Extraer pendiente y umbrales
beta_hat <- coef(fit_polr)[["x"]]
cuts_hat <- fit_polr$zeta # vector con "1|2" y "2|3"

# Transformación a (c15, c25, sigma) en la escala de x
c15_hat   <- as.numeric(cuts_hat[["1|2"]]) / beta_hat
c25_hat   <- as.numeric(cuts_hat[["2|3"]]) / beta_hat
sigma_hat <- 1 / beta_hat

tibble(
  parametro = c("c15_true","c25_true","sigma_true","c15_hat","c25_hat","sigma_hat"),
  valor = c(c15_true, c25_true, sigma_true, c15_hat, c25_hat, sigma_hat)
)
# A tibble: 6 × 2
  parametro  valor
  <chr>      <dbl>
1 c15_true    25  
2 c25_true    55  
3 sigma_true  12  
4 c15_hat     25.1
5 c25_hat     55.8
6 sigma_hat   10.7

5.2.6 Esperanza condicional del número de votos

A partir del modelo, la esperanza condicional de \(y\) es:

\[ \begin{aligned} E(y|x) = & 1 \cdot \operatorname{Pr}(y=1 \mid x)+2 \cdot \operatorname{Pr}(y=2 \mid x)+3 \cdot \operatorname{Pr}(y=3 \mid x) \\ & 1 \cdot (1 - \operatorname{logit}^{-1}\left(\tfrac{x-c_{1.5}}{\sigma}\right)) \\ & + 2 \cdot \left(\operatorname{logit}^{-1}\left(\tfrac{x-c_{1.5}}{\sigma}\right) - \operatorname{logit}^{-1}\left(\tfrac{x-c_{2.5}}{\sigma}\right)\right) \\ & + 3 \cdot \operatorname{logit}^{-1}\left(\tfrac{x-c_{2.5}}{\sigma}\right). \end{aligned} \]

Objetivo del bloque

Definir la función de esperanza condicional \(\mathrm{E}(y\mid x)\) bajo \((c_{1.5},c_{2.5},\sigma)\) y comparar curvas usando parámetros verdaderos vs. estimados.

# E(y|x) según la forma con umbrales en escala x
Ey_fun <- function(x, c15, c25, sigma){
  p15 <- invlogit((x - c15)/sigma)
  p25 <- invlogit((x - c25)/sigma)
  1*(1 - p15) + 2*(p15 - p25) + 3*p25
}

grid_plot <- tibble(x = seq(0, 100, length.out = 400)) |>
  mutate(
    Ey_true = Ey_fun(x, c15_true, c25_true, sigma_true),
    Ey_hat  = Ey_fun(x, c15_hat,  c25_hat,  sigma_hat)
  )

grid_plot
# A tibble: 400 × 3
       x Ey_true Ey_hat
   <dbl>   <dbl>  <dbl>
 1 0        1.12   1.09
 2 0.251    1.12   1.09
 3 0.501    1.13   1.10
 4 0.752    1.13   1.10
 5 1.00     1.13   1.10
 6 1.25     1.13   1.10
 7 1.50     1.14   1.10
 8 1.75     1.14   1.11
 9 2.01     1.14   1.11
10 2.26     1.14   1.11
# ℹ 390 more rows

Objetivo del bloque

Visualizar los datos y las curvas \(\mathrm{E}(y\mid x)\) (verdadera vs. estimada).

# Datos con jitter para y (ordinal 1,2,3)
datos_plot <- datos_sim |>
  mutate(y_jit = jitter(as.numeric(y), amount = 0.08))

ggplot() +
  geom_point(data = datos_plot, aes(x, y_jit), alpha = 0.25) +
  geom_line(data = grid_plot, aes(x, Ey_true), linewidth = 1, linetype = "dashed") +
  geom_line(data = grid_plot, aes(x, Ey_hat),  linewidth = 1) +
  scale_y_continuous(breaks = 1:3, limits = c(0.8, 3.2)) +
  labs(
    title = "Regresión logística ordenada (simulación)",
    subtitle = "Puntos: datos simulados (y con jitter). Líneas: E(y|x) verdadera (discontinua) y estimada (sólida).",
    x = "x (beneficio / puntuación)",
    y = "Categoría / E(y|x)"
  ) +
  theme_minimal()

5.3 Regresión multinormal multinivel

Cada estudiante jugó el juego de votación 30 veces, recibiendo en cada ronda un valor de entrada \(x \in [1,100]\) y emitiendo una respuesta \(y \in {1,2,3}\). Los modelos ajustados inicialmente fueron logísticos ordenados separados por estudiante, pero con solo 30 observaciones por persona, existe una alta incertidumbre.

5.3.1 Extensión a un modelo multinivel

El modelo multinivel permite que los parámetros varíen entre estudiantes \(j\), pero bajo distribuciones comunes:

\[ \begin{aligned} c_{j 1.5} & \sim \mathrm{N}(\mu_{1.5}, \sigma_{1.5}^2), \\ c_{j 2.5} & \sim \mathrm{N}(\mu_{2.5}, \sigma_{2.5}^2), \\ \log \sigma_{j} & \sim \mathrm{N}(\mu_{\log \sigma}, \sigma_{\log \sigma}^2). \end{aligned} \]

  • \(c_{j 1.5}\): punto de corte entre asignar 1 y 2 votos.
  • \(c_{j 2.5}\): punto de corte entre asignar 2 y 3 votos.
  • \(\sigma_{j}\): parámetro de variación que mide cuán estrictamente se sigue una estrategia monótona.

Los hiperparámetros \((\mu_{1.5}, \sigma_{1.5}, \mu_{2.5}, \sigma_{2.5}, \mu_{\log\sigma}, \sigma_{\log\sigma})\) se estiman de los datos. El modelo sin agrupamiento (no pooled) corresponde a fijar \(\sigma_{1.5}=\sigma_{2.5}=\sigma_{\log\sigma}=\infty\).

5.3.2 Interpretación de los parámetros

  • La variación en los puntos de corte refleja diferencias en las estrategias de votación entre estudiantes.
  • El parámetro \(\sigma\) indica el grado de consistencia en la estrategia: valores bajos sugieren decisiones más determinísticas, valores altos mayor aleatoriedad.

5.3.3 Código en R:

# --- Librerías ---
library(tidyverse)
library(MASS)    # polr: modelo logístico ordenado (odds proporcionales)
library(lme4)    # lmer: modelos lineales mixtos

set.seed(123)

# --- 1) Simulación: parámetros por estudiante (modelo generador multinivel) ----
J <- 40                 # número de estudiantes
n_j <- 30               # observaciones por estudiante

# Hiperparámetros "verdaderos" (multinivel)
mu_c15   <- 30
sd_c15   <- 8
mu_c25   <- 60
sd_c25   <- 8
mu_lnsig <- log(10)
sd_lnsig <- 0.35

# Muestra parámetros por estudiante: c15_j, c25_j, sigma_j
pars <- tibble(
  id  = factor(1:J),
  c15 = rnorm(J, mu_c15,   sd_c15),
  c25 = rnorm(J, mu_c25,   sd_c25),
  ls  = rnorm(J, mu_lnsig, sd_lnsig)
) |>
  mutate(
    c25 = pmax(c25, c15 + 2),    # asegurar c25 > c15 (estrategia monótona con separación mínima)
    sigma = exp(ls)
  )

# Función logística inversa
invlogit <- function(x) exp(x)/(1+exp(x))

# Simula datos por estudiante acorde a (c15_j, c25_j, sigma_j)
sim_datos <- pars |>
  group_by(id) |>
  do({
    this <- .
    x <- runif(n_j, 1, 100)  # covariable en [1,100]
    p1 <- 1 - invlogit((x - this$c15)/this$sigma)
    p3 <- invlogit((x - this$c25)/this$sigma)
    p2 <- 1 - p1 - p3
    y  <- map2_int(p1, p2, ~ sample(1:3, size = 1, prob = c(.x, .y, 1-.x-.y)))
    tibble(x, y)
  }) |>
  ungroup()

# --- 2) Ajuste "no pooled": polr por estudiante, obtención de (c15, c25, sigma) estimados ---
ajustes_por_id <- sim_datos |>
  group_by(id) |>
  group_map(~ {
    df <- .x
    # polr en forma estándar: y ~ x, con 2 umbrales (1|2 y 2|3)
    fit <- tryCatch(
      polr(factor(y) ~ x, data = df, method = "logistic", Hess = TRUE),
      error = function(e) NULL
    )
    if (is.null(fit)) {
      tibble(beta_hat = NA_real_, c12_hat = NA_real_, c23_hat = NA_real_,
             c15_hat = NA_real_, c25_hat = NA_real_, sigma_hat = NA_real_)
    } else {
      beta_hat <- as.numeric(coef(fit)[["x"]])
      c12_hat  <- as.numeric(fit$zeta[["1|2"]])
      c23_hat  <- as.numeric(fit$zeta[["2|3"]])
      # Transformación a la parametrización del resumen:
      # c15 = c(1|2)/beta, c25 = c(2|3)/beta, sigma = 1/beta
      c15_hat  <- c12_hat / beta_hat
      c25_hat  <- c23_hat / beta_hat
      sigma_hat<- 1 / beta_hat
      tibble(beta_hat, c12_hat, c23_hat, c15_hat, c25_hat, sigma_hat)
    }
  })
Warning: glm.fit: algorithm did not converge
Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
Warning: glm.fit: algorithm did not converge
Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
Warning: glm.fit: algorithm did not converge
Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
Warning: glm.fit: algorithm did not converge
Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
est_no_pooled <- bind_rows(ajustes_por_id, .id = "id_chr") |>
  mutate(id = factor(as.integer(id_chr))) |>
  dplyr::select(-id_chr)

# Unimos con la "verdad" para evaluación
comp <- pars |>
  dplyr::select(id, c15_true = c15, c25_true = c25, sigma_true = sigma, ls_true = ls) |>
  left_join(est_no_pooled, by = "id") |>
  mutate(lnsigma_hat = log(sigma_hat))

# --- 3) Pooling parcial (multinivel): modelos lineales mixtos sobre parámetros derivados ----
# Idea: modelar c15_hat, c25_hat, log(sigma_hat) con intercepto aleatorio por estudiante alrededor de medias comunes
# (Esto aproxima la jerarquía: c_{j·} ~ Normal(mu, sd^2).)
# Nota: Para robustez, filtramos estimaciones faltantes o infinita



# Instalar si hiciera falta:
# install.packages("ordinal")

library(ordinal)

Attaching package: 'ordinal'
The following object is masked from 'package:dplyr':

    slice
# Usamos los datos fila-a-fila (cada ronda por estudiante):
# sim_datos: columnas id, x, y (como en tu simulación previa)
fit_clmm <- clmm(factor(y) ~ x + (1 | id), data = sim_datos, link = "logit")

summary(fit_clmm)
Cumulative Link Mixed Model fitted with the Laplace approximation

formula: factor(y) ~ x + (1 | id)
data:    sim_datos

 link  threshold nobs logLik  AIC     niter    max.grad cond.H 
 logit flexible  1200 -731.10 1470.21 102(232) 7.57e-03 2.8e+04

Random effects:
 Groups Name        Variance Std.Dev.
 id     (Intercept) 0.2571   0.507   
Number of groups:  id 40 

Coefficients:
  Estimate Std. Error z value Pr(>|z|)    
x 0.097863   0.004211   23.24   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Threshold coefficients:
    Estimate Std. Error z value
1|2   3.1042     0.1950   15.92
2|3   5.7235     0.2636   21.71

Nota: recuerden que el ajuste anterior con clmm estima los parámetros fijos comunes y los efectos aleatorios por estudiante, pero no proporciona directamente las estimaciones individuales de los puntos de corte y sigma por estudiante. Para obtener esas estimaciones, se necesitaría un enfoque bayesiano o un ajuste más complejo que permita extraer los efectos aleatorios y transformarlos adecuadamente.