9  Depuración y aceleración de modelos

Este capítulo aborda estrategias para depurar modelos estadísticos y acelerar la convergencia en métodos de estimación basados en JAGS y R. Se discuten errores comunes de compilación, problemas con los datos e inicializaciones, así como métodos prácticos para mejorar la estabilidad y la velocidad de los algoritmos iterativos. Además, se presentan técnicas para verificar la adecuación del modelo, simulaciones con datos falsos y comparaciones con versiones simplificadas del modelo.

9.1 Depuración y construcción de confianza

El proceso de depuración implica partir de modelos simples (por ejemplo, sin predictores o con agrupación completa) e incrementar progresivamente la complejidad hasta lograr el modelo final deseado. Si un modelo complejo falla, se recomienda reconstruirlo desde cero o simplificarlo hasta encontrar un punto estable.

Los problemas de depuración no solo son técnicos; también ayudan a refinar la comprensión estadística del modelo, identificando versiones más razonables o alternativas.

9.2 Errores comunes en JAGS

Modelo no compila

• Expresiones demasiado complejas en la definición de distribuciones, por ejemplo: \[ y[i] \sim \mathrm{N}(a + b x[i], \tau) \] debe escribirse en dos líneas:

  y[i] ~ dnorm(y_hat[i], tau)
  y_hat[i] <- a + b * x[i]

• Espacios incorrectos en asignaciones (por ejemplo, pow (sigma, -2) debe escribirse pow(sigma, -2)).

• Parámetros indefinidos o duplicados dentro de bucles.

• Variables con múltiples definiciones dentro de un mismo bloque.

Problemas con los datos

• Presencia de NA en datos no modelados.
• Variables incluidas en la lista de datos pero no en el modelo.
• Nombres de variables cambiados o sobrescritos en R.
• Inconsistencias en longitudes o dimensiones de arreglos.
• Valores fuera de rango (por ejemplo, negativos en distribuciones lognormales o fraccionarios en distribuciones binomiales).

Problemas con valores iniciales

• Variables vacías o con valores faltantes.
• Inicializaciones fuera del rango permitido (por ejemplo, varianzas negativas o parámetros con restricciones mal definidas).

Problemas al actualizar

JAGS puede fallar en regiones extremas del espacio de parámetros, como probabilidades cercanas a 0 o 1. Se recomienda usar valores iniciales moderados y, si es necesario, restringir parámetros dentro de límites razonables, por ejemplo: \[ p_{\text{bound}}[i] \leftarrow \max(0, \min(1, p[i])) \]

Resultados incoherentes

Incluso si el modelo converge, los resultados pueden no tener sentido si hay errores conceptuales, como:

• Confundir varianza con precisión (\(\tau = 1 / \sigma^2\)).
• Usar distribuciones no informativas para parámetros que deberían tener jerarquía de grupo.
• Datos enviados erróneamente o mal definidos.

Comparaciones con modelos más simples

Una buena práctica para ganar confianza en modelos multinivel es construirlos progresivamente desde versiones más simples, como:

• Modelos con agrupación completa o sin agrupación.
• Modelos ajustados con lmer() para comparación.
• Exclusión o inclusión gradual de predictores y efectos aleatorios.

Simulación con datos falsos

El método de datos falsos (fake-data simulation) consiste en:

1. Tomar estimaciones del modelo ajustado como “valores verdaderos”.
2. Simular un nuevo conjunto de datos bajo ese modelo.
3. Reajustar el modelo a los datos simulados.
4. Verificar que los parámetros estimados se aproximen a los valores originales.

Verificación del ajuste del modelo

Para evaluar la adecuación del modelo se utilizan:

• Gráficos de residuales.
• Chequeos predictivos posteriores (PPC), comparando datos observados con datos simulados desde el modelo ajustado. Esta comparación puede ser numérica o visual, y su objetivo es confirmar que el modelo reproduce adecuadamente las características esenciales de los datos observados.

Dificultades inesperadas en JAGS

Incluso modelos simples pueden fallar debido a:

• Colinealidad entre predictores.
• Malas inicializaciones o parametrizaciones. Como solución, se recomienda centrar los predictores y reparametrizar el modelo hasta lograr estabilidad.

9.3 Métodos generales para reducir requerimientos computacionales

Dos vías principales

1. Reducir el tiempo por iteración.
2. Reducir el número de iteraciones hasta convergencia.

En secciones posteriores se amplían estrategias específicas para acelerar el mezclado de los Gibbs samplers en modelos multinivel.

Muestreo de datos para acelerar la computación

Cuando el conjunto de datos es muy grande o el número de parámetros es alto, se puede trabajar con submuestras aleatorias:

subset <- sample(n, n/10)
n <- length(subset)
y <- y[subset]
X <- X[subset, ]
state <- state[subset]

También puede emplearse muestreo por conglomerados, seleccionando solo algunos grupos y una fracción de las observaciones dentro de cada grupo. Esto reduce tanto el número de datos como el de parámetros, aunque no se recomienda reducir el número de grupos a menos de cinco, pues dificulta la estimación de varianzas a nivel de grupo.

Reducción de salida (thinning) para ahorrar memoria

Cuando la autocorrelación entre iteraciones es alta, puede usarse thinning, conservando solo cada \(k\)-ésima muestra:

• Reduce el tamaño de almacenamiento.
• Aumenta la independencia efectiva entre muestras. La función ahora jags() suele configurarse para conservar aproximadamente 1000 muestras representativas.

Saber cuándo detenerse

Si tras muchas iteraciones no hay convergencia, se recomienda:

• Reformular el modelo según las estrategias de este capítulo.
• Probar versiones más simples mientras se desarrolla el modelo completo.

Esta práctica permite entender mejor los patrones de los datos y establecer expectativas razonables antes de pasar a modelos complejos.

9.4 Transformaciones lineales simples

Cuando los parámetros del modelo están altamente correlacionados, el Gibbs sampler converge lentamente. Un caso típico aparece entre el intercepto y las pendientes cuando los predictores no están centrados en cero. La solución práctica es centrar los predictores antes de incluirlos en el modelo.

9.4.1 Modelo de referencia y reparametrización por centrado

Partimos del modelo de regresión lineal \[ y_i \sim \mathrm{N}\bigl(\alpha+\beta_1 X_{i1}+\beta_2 X_{i2},\sigma_y^2\bigr), \] y definimos los predictores centrados \[ z_1 = x_1 - \overline{x}_1, \qquad z_2 = x_2 - \overline{x}_2. \] Al expresar el modelo en función de \(Z\) se obtiene \[ \begin{aligned} y_i &= \alpha + \beta_1 Z_{i1} + \beta_2 Z_{i2} + \epsilon_i \\ &= \alpha + \beta_1 (X_{i1}-\overline{X}_1) + \beta_2 (X_{i2}-\overline{X}_2) + \epsilon_i \\ &= \bigl(\alpha - \beta_1 \overline{X}_1 - \beta_2 \overline{X}_2\bigr) + \beta_1 X_{i1} + \beta_2 X_{i2} + \epsilon_i. \end{aligned} \] Por lo tanto, el intercepto en la escala original es \[ \alpha^\star =\alpha - \beta_1 \overline{X}_1 - \beta_2 \overline{X}_2, \] y las pendientes permanecen inalteradas.

9.5 Parámetros redundantes e identificabilidad en modelos jerárquicos

En regresión clásica solo pueden incluirse \(J-1\) indicadores de grupo; en modelos multinivel se pueden incluir los \(J\) coeficientes porque provienen de una distribución con varianza finita. Aquí, la no identificabilidad se usa con fines computacionales (acelerar la convergencia), incluso dentro de un modelo jerárquico.

9.5.1 Modelo anidado simple (versión base)

Formulación: \[ \begin{aligned} y_{i} &\sim \mathrm{N}\big(\mu+\eta_{j[i]},\sigma_{y}^{2}\big), \quad i=1,\ldots,n,\\ \eta_{j} &\sim \mathrm{N}\big(0,\sigma_{\eta}^{2}\big), \quad j=1,\ldots,J. \end{aligned} \]

Carga de datos:

srrs2 <- read.table("../ARM_Data/radon/srrs2.dat", header=TRUE, sep=",")
mn <- srrs2$state == "MN"
radon <- srrs2$activity[mn]
y <- log(ifelse(radon == 0, 0.1, radon))
n <- length(radon)
x <- srrs2$floor[mn]  # 0 for basement, 1 for first floor

srrs2.fips <- srrs2$stfips * 1000 + srrs2$cntyfips
county.name <- as.vector(srrs2$county[mn])
uniq.name <- unique(county.name)
J <- length(uniq.name)
county <- rep(NA, J)
for (i in 1:J) {
  county[county.name == uniq.name[i]] <- i
}

srrs2.fips <- srrs2$stfips*1000 + srrs2$cntyfips
cty <- read.table ("../ARM_Data/radon/cty.dat", header=T, sep=",")
usa.fips <- 1000*cty[,"stfips"] + cty[,"ctfips"]
usa.rows <- match (unique(srrs2.fips[mn]), usa.fips)
uranium <- cty[usa.rows,"Uppm"]
u <- log (uranium)

u.full <- u[county]

data_jags <- list(y = y, x = x, county = county, n = n, J = J)

data_jags$u <- u.full

Ajuste:

# Load library
library(R2jags)

Loading required package: rjags

Loading required package: coda

Linked to JAGS 4.3.0

Loaded modules: basemod,bugs

Attaching package: 'R2jags'

The following object is masked from 'package:coda':

    traceplot

# Define data and initial values for JAGS
data_jags <- list(y = y, county = county, n = length(y), n.county = length(unique(county)))
inits <- function() {
  list(mu = rnorm(1), sigma.y = runif(1), sigma.eta = runif(1))
}
params <- c("mu", "eta", "sigma.y", "sigma.eta")

# Fit the model
jags_fit <- jags(data = data_jags, inits = inits, parameters.to.save = params, model.file = "codigoJAGS/radon_model_simplified.jags", n.chains = 3, n.iter = 5000, n.burnin = 1000, n.thin = 10)

module glm loaded

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 919
   Unobserved stochastic nodes: 88
   Total graph size: 2020

Initializing model

# Summary and plot of results
print(jags_fit)

Inference for Bugs model at "codigoJAGS/radon_model_simplified.jags", fit using jags,
 3 chains, each with 5000 iterations (first 1000 discarded), n.thin = 10
 n.sims = 1200 iterations saved. Running time = 10.295 secs
           mu.vect sd.vect     2.5%      25%      50%      75%    97.5%  Rhat
eta[1]      -0.250   0.258   -0.766   -0.428   -0.237   -0.068    0.245 1.000
eta[2]      -0.424   0.112   -0.642   -0.499   -0.424   -0.350   -0.204 1.001
eta[3]      -0.072   0.255   -0.570   -0.235   -0.078    0.093    0.423 1.001
eta[4]      -0.097   0.224   -0.507   -0.239   -0.107    0.049    0.386 1.002
eta[5]      -0.028   0.247   -0.497   -0.200   -0.032    0.135    0.468 1.003
eta[6]       0.069   0.260   -0.451   -0.098    0.077    0.237    0.596 1.002
eta[7]       0.401   0.181    0.061    0.275    0.406    0.520    0.786 1.007
eta[8]       0.119   0.257   -0.379   -0.049    0.114    0.294    0.619 1.000
eta[9]      -0.228   0.202   -0.632   -0.358   -0.227   -0.101    0.156 1.000
eta[10]     -0.059   0.232   -0.525   -0.221   -0.056    0.106    0.391 1.003
eta[11]      0.034   0.225   -0.406   -0.118    0.036    0.182    0.503 1.002
eta[12]      0.160   0.248   -0.324   -0.012    0.158    0.317    0.650 1.002
eta[13]     -0.131   0.219   -0.572   -0.272   -0.131    0.013    0.300 1.001
eta[14]      0.312   0.181   -0.023    0.188    0.308    0.433    0.661 1.006
eta[15]     -0.122   0.253   -0.643   -0.286   -0.120    0.047    0.364 1.000
eta[16]     -0.147   0.275   -0.715   -0.326   -0.139    0.049    0.369 1.001
eta[17]     -0.220   0.252   -0.717   -0.385   -0.210   -0.044    0.274 1.004
eta[18]     -0.244   0.193   -0.628   -0.369   -0.242   -0.115    0.135 1.001
eta[19]     -0.020   0.103   -0.220   -0.092   -0.018    0.056    0.170 1.001
eta[20]      0.153   0.268   -0.367   -0.025    0.150    0.332    0.689 1.000
eta[21]      0.202   0.209   -0.211    0.059    0.201    0.352    0.598 1.001
eta[22]     -0.387   0.238   -0.905   -0.540   -0.382   -0.234    0.071 1.000
eta[23]     -0.060   0.274   -0.586   -0.236   -0.058    0.116    0.515 1.000
eta[24]      0.371   0.211   -0.029    0.231    0.368    0.512    0.788 1.000
eta[25]      0.367   0.184    0.033    0.237    0.361    0.497    0.733 1.000
eta[26]     -0.029   0.092   -0.205   -0.087   -0.029    0.031    0.153 1.000
eta[27]      0.094   0.225   -0.348   -0.059    0.093    0.250    0.524 1.002
eta[28]     -0.218   0.244   -0.679   -0.376   -0.223   -0.051    0.256 1.002
eta[29]     -0.085   0.268   -0.604   -0.258   -0.088    0.100    0.418 1.001
eta[30]     -0.244   0.192   -0.630   -0.371   -0.237   -0.112    0.118 1.000
eta[31]      0.303   0.245   -0.176    0.128    0.307    0.467    0.797 1.002
eta[32]     -0.038   0.254   -0.534   -0.208   -0.044    0.124    0.489 1.000
eta[33]      0.283   0.251   -0.199    0.109    0.275    0.455    0.792 1.005
eta[34]     -0.067   0.264   -0.582   -0.234   -0.070    0.094    0.473 1.001
eta[35]     -0.465   0.237   -0.931   -0.628   -0.460   -0.298   -0.029 1.005
eta[36]      0.312   0.278   -0.214    0.127    0.305    0.488    0.879 1.001
eta[37]     -0.574   0.221   -1.020   -0.728   -0.565   -0.419   -0.171 1.001
eta[38]      0.084   0.246   -0.386   -0.086    0.082    0.253    0.559 1.001
eta[39]      0.117   0.232   -0.334   -0.034    0.115    0.273    0.569 1.001
eta[40]      0.311   0.252   -0.147    0.134    0.303    0.481    0.800 1.003
eta[41]      0.311   0.209   -0.095    0.174    0.311    0.445    0.717 1.004
eta[42]     -0.008   0.292   -0.604   -0.207    0.001    0.183    0.568 1.006
eta[43]     -0.059   0.203   -0.470   -0.193   -0.051    0.072    0.343 1.001
eta[44]     -0.200   0.210   -0.633   -0.332   -0.197   -0.050    0.188 1.003
eta[45]     -0.160   0.185   -0.536   -0.280   -0.159   -0.034    0.202 1.000
eta[46]     -0.036   0.237   -0.512   -0.185   -0.044    0.113    0.426 1.001
eta[47]     -0.172   0.270   -0.703   -0.343   -0.164    0.012    0.365 1.000
eta[48]     -0.148   0.200   -0.560   -0.276   -0.151   -0.016    0.256 1.001
eta[49]      0.178   0.187   -0.197    0.051    0.181    0.302    0.545 1.000
eta[50]      0.145   0.282   -0.421   -0.032    0.137    0.328    0.683 1.002
eta[51]      0.324   0.255   -0.141    0.149    0.302    0.489    0.861 1.003
eta[52]      0.203   0.273   -0.302    0.011    0.202    0.379    0.728 1.001
eta[53]     -0.096   0.258   -0.624   -0.259   -0.090    0.082    0.405 1.000
eta[54]     -0.077   0.154   -0.380   -0.180   -0.074    0.025    0.227 1.001
eta[55]      0.017   0.208   -0.389   -0.120    0.014    0.160    0.433 1.000
eta[56]     -0.204   0.251   -0.728   -0.361   -0.198   -0.034    0.285 1.000
eta[57]     -0.332   0.240   -0.810   -0.498   -0.329   -0.162    0.134 1.001
eta[58]      0.148   0.240   -0.316   -0.011    0.151    0.300    0.654 1.002
eta[59]      0.011   0.253   -0.466   -0.167    0.009    0.177    0.550 1.003
eta[60]     -0.015   0.277   -0.580   -0.207   -0.012    0.176    0.495 1.001
eta[61]     -0.181   0.135   -0.434   -0.272   -0.183   -0.094    0.080 1.001
eta[62]      0.228   0.243   -0.237    0.062    0.228    0.395    0.697 1.001
eta[63]      0.035   0.257   -0.485   -0.135    0.045    0.202    0.540 1.001
eta[64]      0.291   0.192   -0.064    0.151    0.278    0.427    0.667 1.003
eta[65]     -0.015   0.270   -0.577   -0.189   -0.011    0.158    0.497 1.003
eta[66]     -0.042   0.184   -0.402   -0.164   -0.048    0.083    0.321 1.003
eta[67]      0.171   0.187   -0.187    0.044    0.166    0.297    0.545 1.006
eta[68]     -0.123   0.208   -0.543   -0.266   -0.127    0.018    0.293 1.000
eta[69]     -0.036   0.242   -0.493   -0.204   -0.038    0.119    0.465 1.001
eta[70]     -0.517   0.085   -0.683   -0.574   -0.514   -0.460   -0.351 1.001
eta[71]      0.054   0.145   -0.216   -0.045    0.052    0.157    0.340 1.000
eta[72]      0.153   0.208   -0.240    0.009    0.143    0.286    0.575 1.001
eta[73]      0.111   0.272   -0.414   -0.077    0.103    0.290    0.646 1.006
eta[74]     -0.123   0.249   -0.601   -0.292   -0.126    0.043    0.348 1.000
eta[75]      0.052   0.259   -0.438   -0.112    0.046    0.213    0.584 1.002
eta[76]      0.185   0.242   -0.281    0.028    0.192    0.344    0.661 1.001
eta[77]      0.202   0.229   -0.227    0.046    0.197    0.361    0.644 1.002
eta[78]     -0.126   0.236   -0.575   -0.288   -0.125    0.033    0.345 1.002
eta[79]     -0.327   0.254   -0.837   -0.491   -0.316   -0.149    0.153 1.001
eta[80]     -0.059   0.119   -0.298   -0.137   -0.055    0.021    0.179 1.002
eta[81]      0.304   0.269   -0.241    0.124    0.309    0.479    0.843 1.001
eta[82]      0.128   0.300   -0.451   -0.074    0.132    0.322    0.713 1.002
eta[83]      0.105   0.182   -0.251   -0.021    0.102    0.233    0.452 1.002
eta[84]      0.188   0.190   -0.185    0.060    0.189    0.308    0.570 1.006
eta[85]     -0.039   0.284   -0.571   -0.225   -0.046    0.151    0.507 1.001
mu           1.315   0.051    1.213    1.281    1.317    1.350    1.414 1.000
sigma.eta    0.315   0.049    0.225    0.281    0.314    0.346    0.415 1.002
sigma.y      0.799   0.020    0.762    0.786    0.799    0.812    0.838 1.001
deviance  2194.485  12.955 2170.911 2185.809 2193.556 2203.492 2219.916 1.000
          n.eff
eta[1]     1200
eta[2]     1200
eta[3]     1200
eta[4]     1100
eta[5]      560
eta[6]     1200
eta[7]      260
eta[8]     1200
eta[9]     1200
eta[10]     810
eta[11]     760
eta[12]     970
eta[13]    1200
eta[14]     590
eta[15]    1200
eta[16]    1200
eta[17]     500
eta[18]    1200
eta[19]    1200
eta[20]    1200
eta[21]    1200
eta[22]    1200
eta[23]    1200
eta[24]    1200
eta[25]    1200
eta[26]    1200
eta[27]     810
eta[28]     800
eta[29]    1200
eta[30]    1200
eta[31]     890
eta[32]    1200
eta[33]     380
eta[34]    1200
eta[35]     460
eta[36]    1200
eta[37]    1200
eta[38]    1200
eta[39]    1200
eta[40]     670
eta[41]    1200
eta[42]     530
eta[43]    1200
eta[44]     690
eta[45]    1200
eta[46]    1200
eta[47]    1200
eta[48]    1200
eta[49]    1200
eta[50]     760
eta[51]     720
eta[52]    1200
eta[53]    1200
eta[54]    1200
eta[55]    1200
eta[56]    1200
eta[57]    1200
eta[58]    1200
eta[59]     570
eta[60]    1200
eta[61]    1200
eta[62]    1200
eta[63]    1200
eta[64]     570
eta[65]     590
eta[66]     630
eta[67]     350
eta[68]    1200
eta[69]    1200
eta[70]    1200
eta[71]    1200
eta[72]    1200
eta[73]     310
eta[74]    1200
eta[75]    1100
eta[76]    1200
eta[77]     880
eta[78]    1000
eta[79]    1200
eta[80]     810
eta[81]    1200
eta[82]    1200
eta[83]     890
eta[84]    1200
eta[85]    1200
mu         1200
sigma.eta  1100
sigma.y    1200
deviance   1200

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule: pV = var(deviance)/2)
pV = 84.0 and DIC = 2278.5
DIC is an estimate of expected predictive error (lower deviance is better).

Diagnósticos:

library(CalvinBayes)

Loading required package: dplyr

Attaching package: 'dplyr'

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

Loading required package: ggplot2

Loading required package: ggformula

Loading required package: scales

Loading required package: ggiraph

Loading required package: ggridges

New to ggformula?  Try the tutorials: 
    learnr::run_tutorial("introduction", package = "ggformula")
    learnr::run_tutorial("refining", package = "ggformula")

Loading required package: bayesplot

This is bayesplot version 1.14.0

- Online documentation and vignettes at mc-stan.org/bayesplot

- bayesplot theme set to bayesplot::theme_default()

   * Does _not_ affect other ggplot2 plots

   * See ?bayesplot_theme_set for details on theme setting

Attaching package: 'CalvinBayes'

The following object is masked from 'package:bayesplot':

    rhat

The following object is masked from 'package:datasets':

    HairEyeColor

diagMCMC(as.mcmc(jags_fit),parName = 'mu')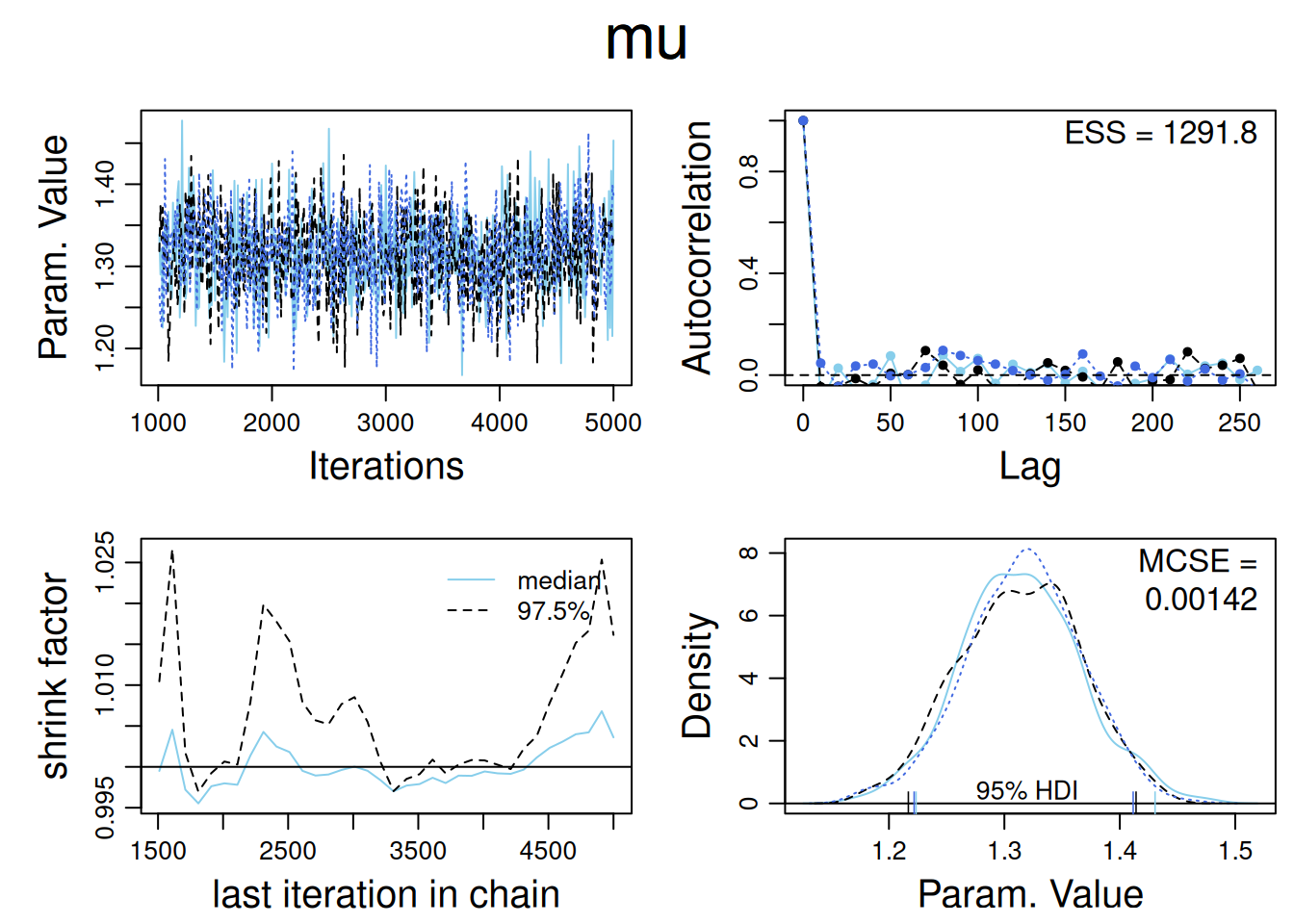

9.5.2 Modelo anidado con parámetro redundante (aceleración de convergencia)

Para evitar que la cadena “se atasque” con \(\eta\) lejos de cero, se agrega un parámetro redundante \(\mu_{\eta}\) y se centran los efectos: \[ \mu^{\text{adj}} = \mu + \overline{\eta},\qquad \eta^{\text{adj}}_j = \eta_j - \overline{\eta}. \]

inits <- function() {
  list(mu = rnorm(1), sigma.y = runif(1), sigma.eta = runif(1), mu.eta = rnorm(1))
}
params <- c("mu.adj", "eta.adj", "sigma.y", "sigma.eta")

# Fit the model
jags_fit <- jags(data = data_jags, inits = inits, parameters.to.save = params, model.file = "codigoJAGS/radon_model_simplified_adjusted.jags", n.chains = 3, n.iter = 5000, n.burnin = 1000, n.thin = 10)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 919
   Unobserved stochastic nodes: 89
   Total graph size: 2109

Initializing model

# Summary and plot of results
print(jags_fit)

Inference for Bugs model at "codigoJAGS/radon_model_simplified_adjusted.jags", fit using jags,
 3 chains, each with 5000 iterations (first 1000 discarded), n.thin = 10
 n.sims = 1200 iterations saved. Running time = 8.976 secs
             mu.vect sd.vect     2.5%      25%      50%      75%    97.5%  Rhat
eta.adj[1]    -0.243   0.258   -0.779   -0.411   -0.240   -0.064    0.254 1.001
eta.adj[2]    -0.418   0.112   -0.638   -0.490   -0.419   -0.343   -0.197 1.004
eta.adj[3]    -0.084   0.258   -0.579   -0.250   -0.093    0.090    0.425 1.000
eta.adj[4]    -0.083   0.224   -0.543   -0.219   -0.076    0.065    0.329 1.001
eta.adj[5]    -0.016   0.247   -0.523   -0.172   -0.030    0.156    0.499 1.002
eta.adj[6]     0.059   0.255   -0.443   -0.115    0.060    0.234    0.555 1.002
eta.adj[7]     0.410   0.183    0.053    0.283    0.403    0.534    0.782 1.000
eta.adj[8]     0.119   0.250   -0.371   -0.044    0.113    0.281    0.628 1.000
eta.adj[9]    -0.231   0.197   -0.637   -0.362   -0.229   -0.103    0.175 1.001
eta.adj[10]   -0.053   0.219   -0.497   -0.197   -0.056    0.093    0.352 1.002
eta.adj[11]    0.046   0.230   -0.417   -0.098    0.052    0.195    0.511 1.002
eta.adj[12]    0.149   0.232   -0.293   -0.008    0.152    0.301    0.613 1.002
eta.adj[13]   -0.123   0.221   -0.585   -0.276   -0.112    0.030    0.300 1.001
eta.adj[14]    0.316   0.177   -0.018    0.188    0.316    0.434    0.678 1.002
eta.adj[15]   -0.122   0.250   -0.623   -0.297   -0.121    0.046    0.365 1.000
eta.adj[16]   -0.144   0.285   -0.702   -0.334   -0.139    0.040    0.419 1.012
eta.adj[17]   -0.210   0.247   -0.681   -0.374   -0.207   -0.037    0.251 1.001
eta.adj[18]   -0.235   0.186   -0.594   -0.365   -0.238   -0.108    0.124 1.003
eta.adj[19]   -0.017   0.097   -0.218   -0.082   -0.013    0.049    0.169 1.000
eta.adj[20]    0.153   0.272   -0.382   -0.031    0.146    0.327    0.702 1.003
eta.adj[21]    0.193   0.206   -0.218    0.047    0.191    0.334    0.597 1.000
eta.adj[22]   -0.386   0.232   -0.867   -0.537   -0.378   -0.236    0.041 1.001
eta.adj[23]   -0.056   0.271   -0.573   -0.233   -0.059    0.118    0.476 1.000
eta.adj[24]    0.364   0.208   -0.042    0.226    0.356    0.498    0.790 1.000
eta.adj[25]    0.357   0.182   -0.002    0.238    0.357    0.476    0.712 1.002
eta.adj[26]   -0.026   0.081   -0.185   -0.079   -0.025    0.028    0.134 1.001
eta.adj[27]    0.102   0.221   -0.350   -0.040    0.098    0.246    0.533 1.001
eta.adj[28]   -0.212   0.236   -0.666   -0.368   -0.216   -0.045    0.232 1.003
eta.adj[29]   -0.084   0.258   -0.582   -0.263   -0.088    0.095    0.390 1.000
eta.adj[30]   -0.239   0.195   -0.631   -0.379   -0.238   -0.109    0.135 1.003
eta.adj[31]    0.290   0.241   -0.170    0.130    0.289    0.453    0.780 1.000
eta.adj[32]   -0.026   0.246   -0.529   -0.203   -0.020    0.141    0.440 1.000
eta.adj[33]    0.273   0.249   -0.207    0.104    0.268    0.444    0.780 1.000
eta.adj[34]   -0.053   0.252   -0.531   -0.238   -0.050    0.112    0.446 1.000
eta.adj[35]   -0.462   0.212   -0.881   -0.603   -0.460   -0.313   -0.061 1.000
eta.adj[36]    0.280   0.276   -0.273    0.100    0.262    0.454    0.842 1.000
eta.adj[37]   -0.570   0.219   -1.009   -0.712   -0.566   -0.415   -0.146 1.003
eta.adj[38]    0.084   0.252   -0.394   -0.089    0.079    0.251    0.584 1.000
eta.adj[39]    0.122   0.226   -0.296   -0.035    0.117    0.281    0.543 1.001
eta.adj[40]    0.308   0.250   -0.158    0.136    0.295    0.477    0.805 1.001
eta.adj[41]    0.298   0.216   -0.097    0.154    0.289    0.440    0.748 1.000
eta.adj[42]    0.015   0.282   -0.540   -0.172    0.014    0.201    0.585 1.001
eta.adj[43]   -0.065   0.198   -0.458   -0.203   -0.059    0.067    0.329 1.000
eta.adj[44]   -0.198   0.210   -0.619   -0.343   -0.193   -0.060    0.216 1.000
eta.adj[45]   -0.153   0.185   -0.508   -0.281   -0.149   -0.020    0.199 1.005
eta.adj[46]   -0.043   0.228   -0.484   -0.190   -0.036    0.112    0.404 1.000
eta.adj[47]   -0.186   0.273   -0.736   -0.371   -0.185    0.009    0.310 1.001
eta.adj[48]   -0.140   0.196   -0.518   -0.272   -0.137   -0.005    0.226 1.002
eta.adj[49]    0.180   0.179   -0.163    0.064    0.179    0.294    0.534 1.002
eta.adj[50]    0.149   0.290   -0.406   -0.048    0.146    0.332    0.720 1.001
eta.adj[51]    0.325   0.253   -0.134    0.144    0.322    0.500    0.820 1.002
eta.adj[52]    0.191   0.262   -0.310    0.020    0.185    0.364    0.703 1.002
eta.adj[53]   -0.097   0.255   -0.613   -0.259   -0.095    0.067    0.400 1.000
eta.adj[54]   -0.071   0.148   -0.351   -0.173   -0.069    0.031    0.218 1.005
eta.adj[55]    0.022   0.201   -0.378   -0.114    0.019    0.154    0.421 1.004
eta.adj[56]   -0.231   0.263   -0.777   -0.403   -0.228   -0.063    0.288 1.003
eta.adj[57]   -0.311   0.232   -0.792   -0.453   -0.295   -0.156    0.120 1.000
eta.adj[58]    0.136   0.244   -0.320   -0.035    0.137    0.305    0.617 1.002
eta.adj[59]    0.018   0.241   -0.459   -0.136    0.012    0.182    0.486 1.002
eta.adj[60]   -0.015   0.273   -0.592   -0.179   -0.011    0.161    0.526 1.001
eta.adj[61]   -0.182   0.132   -0.444   -0.269   -0.184   -0.089    0.071 1.001
eta.adj[62]    0.217   0.228   -0.249    0.072    0.220    0.369    0.660 1.001
eta.adj[63]    0.032   0.253   -0.459   -0.134    0.024    0.196    0.533 1.001
eta.adj[64]    0.293   0.190   -0.063    0.162    0.290    0.421    0.661 1.000
eta.adj[65]    0.006   0.270   -0.519   -0.180    0.008    0.187    0.539 1.000
eta.adj[66]   -0.043   0.175   -0.391   -0.161   -0.042    0.077    0.296 1.002
eta.adj[67]    0.173   0.177   -0.168    0.056    0.173    0.287    0.533 1.003
eta.adj[68]   -0.117   0.206   -0.528   -0.255   -0.114    0.032    0.269 1.000
eta.adj[69]   -0.015   0.249   -0.499   -0.182   -0.018    0.160    0.459 1.001
eta.adj[70]   -0.510   0.079   -0.662   -0.564   -0.510   -0.457   -0.349 1.001
eta.adj[71]    0.051   0.144   -0.234   -0.042    0.054    0.149    0.330 1.002
eta.adj[72]    0.153   0.196   -0.232    0.026    0.151    0.280    0.548 1.000
eta.adj[73]    0.106   0.273   -0.407   -0.080    0.108    0.282    0.668 1.000
eta.adj[74]   -0.125   0.245   -0.609   -0.287   -0.122    0.029    0.346 1.000
eta.adj[75]    0.050   0.253   -0.490   -0.114    0.050    0.221    0.535 1.001
eta.adj[76]    0.191   0.244   -0.285    0.029    0.191    0.348    0.676 1.001
eta.adj[77]    0.195   0.229   -0.231    0.044    0.184    0.346    0.675 1.006
eta.adj[78]   -0.135   0.231   -0.583   -0.291   -0.133    0.027    0.318 1.004
eta.adj[79]   -0.326   0.258   -0.840   -0.505   -0.323   -0.143    0.170 1.001
eta.adj[80]   -0.055   0.112   -0.274   -0.127   -0.053    0.022    0.149 1.000
eta.adj[81]    0.309   0.261   -0.193    0.129    0.314    0.488    0.803 1.003
eta.adj[82]    0.126   0.299   -0.456   -0.072    0.122    0.313    0.733 1.000
eta.adj[83]    0.095   0.177   -0.238   -0.032    0.097    0.216    0.446 1.003
eta.adj[84]    0.178   0.175   -0.171    0.053    0.175    0.300    0.520 1.001
eta.adj[85]   -0.030   0.275   -0.589   -0.206   -0.035    0.150    0.506 1.002
mu.adj         1.311   0.036    1.245    1.286    1.311    1.337    1.380 1.004
sigma.eta      0.313   0.051    0.222    0.277    0.311    0.346    0.420 1.000
sigma.y        0.799   0.020    0.763    0.785    0.799    0.812    0.839 1.004
deviance    2195.337  13.106 2170.905 2185.723 2194.717 2204.017 2223.706 1.000
            n.eff
eta.adj[1]   1200
eta.adj[2]    840
eta.adj[3]   1200
eta.adj[4]   1200
eta.adj[5]    820
eta.adj[6]    790
eta.adj[7]   1200
eta.adj[8]   1200
eta.adj[9]   1200
eta.adj[10]  1100
eta.adj[11]  1000
eta.adj[12]   820
eta.adj[13]  1200
eta.adj[14]  1200
eta.adj[15]  1200
eta.adj[16]   170
eta.adj[17]  1200
eta.adj[18]   540
eta.adj[19]  1200
eta.adj[20]   550
eta.adj[21]  1200
eta.adj[22]  1200
eta.adj[23]  1200
eta.adj[24]  1200
eta.adj[25]  1000
eta.adj[26]  1200
eta.adj[27]  1200
eta.adj[28]   940
eta.adj[29]  1200
eta.adj[30]   580
eta.adj[31]  1200
eta.adj[32]  1200
eta.adj[33]  1200
eta.adj[34]  1200
eta.adj[35]  1200
eta.adj[36]  1200
eta.adj[37]   810
eta.adj[38]  1200
eta.adj[39]  1200
eta.adj[40]  1200
eta.adj[41]  1200
eta.adj[42]  1200
eta.adj[43]  1200
eta.adj[44]  1200
eta.adj[45]   420
eta.adj[46]  1200
eta.adj[47]  1200
eta.adj[48]  1200
eta.adj[49]  1200
eta.adj[50]  1200
eta.adj[51]  1200
eta.adj[52]  1100
eta.adj[53]  1200
eta.adj[54]   370
eta.adj[55]   470
eta.adj[56]   770
eta.adj[57]  1200
eta.adj[58]   850
eta.adj[59]  1100
eta.adj[60]  1200
eta.adj[61]  1200
eta.adj[62]  1200
eta.adj[63]  1200
eta.adj[64]  1200
eta.adj[65]  1200
eta.adj[66]  1100
eta.adj[67]   640
eta.adj[68]  1200
eta.adj[69]  1200
eta.adj[70]  1200
eta.adj[71]  1200
eta.adj[72]  1200
eta.adj[73]  1200
eta.adj[74]  1200
eta.adj[75]  1200
eta.adj[76]  1200
eta.adj[77]   350
eta.adj[78]   460
eta.adj[79]  1200
eta.adj[80]  1200
eta.adj[81]   550
eta.adj[82]  1200
eta.adj[83]   720
eta.adj[84]  1200
eta.adj[85]   780
mu.adj        490
sigma.eta    1200
sigma.y      1200
deviance     1200

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule: pV = var(deviance)/2)
pV = 86.0 and DIC = 2281.3
DIC is an estimate of expected predictive error (lower deviance is better).

Diagnósticos:

diagMCMC(as.mcmc(jags_fit),parName = 'mu.adj')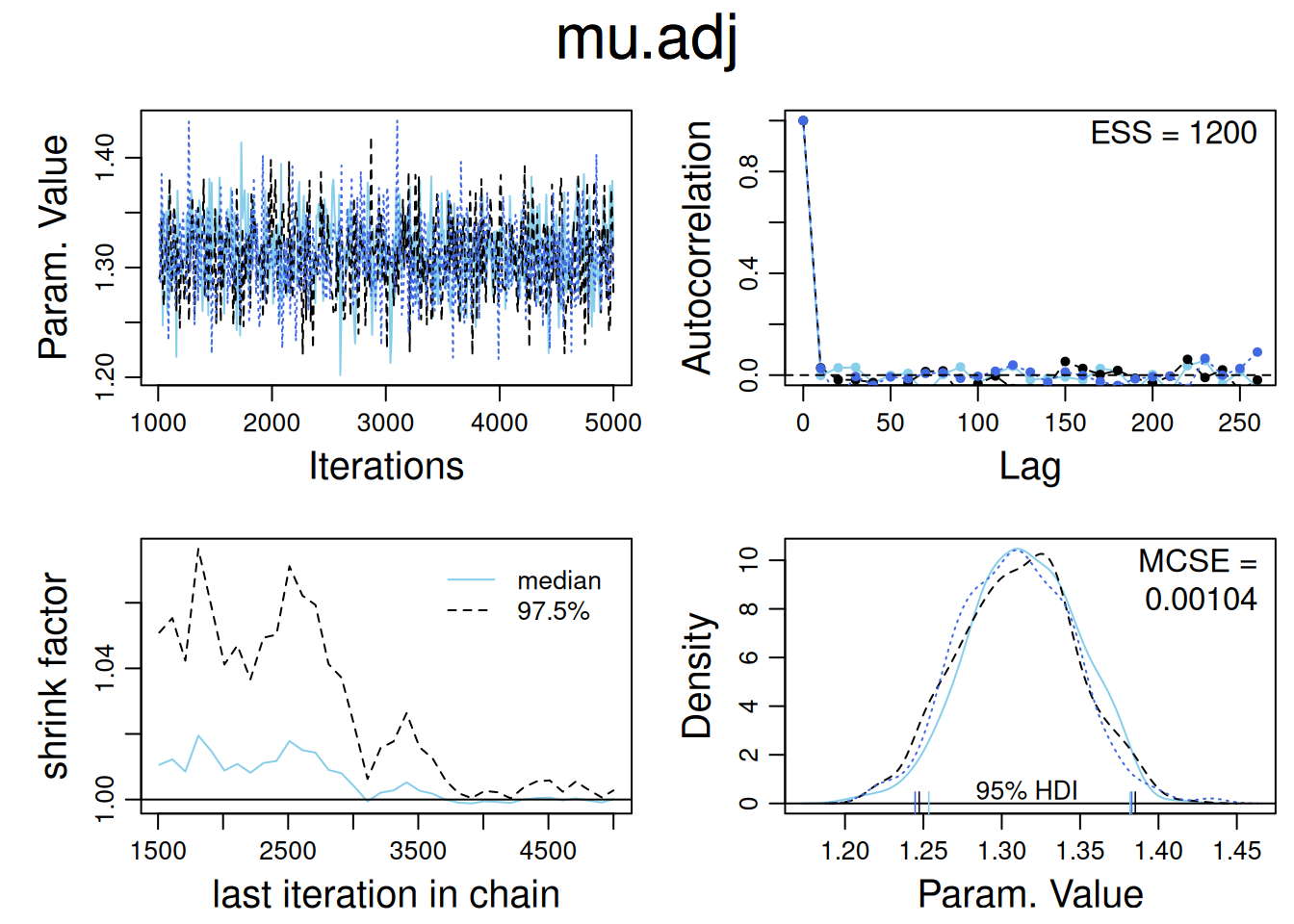

9.5.3 Parámetros redundantes en modelo no anidado (simulador de vuelo)

Prioris con medias redundantes (no identificables individualmente, útiles computacionalmente): \[ \gamma_j \sim \mathrm{N}(\mu_\gamma,\sigma_\gamma^2),\quad j=1,\ldots,J;\qquad \delta_k \sim \mathrm{N}(\mu_\delta,\sigma_\delta^2),\quad k=1,\ldots,K. \]

library("arm")

Loading required package: MASS

Attaching package: 'MASS'

The following object is masked from 'package:dplyr':

    select

Loading required package: Matrix

Loading required package: lme4

arm (Version 1.14-4, built: 2024-4-1)

Working directory is /home/lbarboza/Dropbox/Cursos/Actuales/SP1653_2025/NotasClase/ModelosMixtos

Attaching package: 'arm'

The following object is masked from 'package:scales':

    rescale

The following object is masked from 'package:R2jags':

    traceplot

The following object is masked from 'package:coda':

    traceplot

pilots <- read.table ("../ARM_Data/pilots/pilots.dat", header=TRUE)
attach (pilots)
group.names <- as.vector(unique(group))
scenario.names <- as.vector(unique(scenario))
n.group <- length(group.names)
n.scenario <- length(scenario.names)
successes <- NULL
failures <- NULL
group.id <- NULL
scenario.id <- NULL
for (j in 1:n.group){
  for (k in 1:n.scenario){
    ok <- group==group.names[j] & scenario==scenario.names[k]    
    successes <- c (successes, sum(recovered[ok]==1,na.rm=T))
    failures <- c (failures, sum(recovered[ok]==0,na.rm=T))
    group.id <- c (group.id, j)
    scenario.id <- c (scenario.id, k)
  }
}

y <- successes/(successes+failures)

Ajuste:

# Prepare data for JAGS
data_jags <- list(
  y = y,
  treatment = group.id,
  airport = scenario.id,
  n = length(y),
  n.treatment = length(unique(group.id)),
  n.airport = length(unique(scenario.id))
)

# Initial values
inits <- function() {
  list(
    mu = rnorm(1),
    sigma.y = runif(1),
    sigma.g = runif(1),
    sigma.d = runif(1),
    mu.g = rnorm(1),
    mu.d = rnorm(1)
  )
}

# Parameters to monitor
params <- c("mu.adj", "g.adj", "d.adj", "mu.g", "mu.d", "sigma.y", "sigma.g", "sigma.d")

# Fit the model with JAGS
jags_fit <- jags(
  data = data_jags, 
  inits = inits, 
  parameters.to.save = params, 
  model.file = "./codigoJAGS/pilots_adjusted.jags",
  n.chains = 3, 
  n.iter = 5000, 
  n.burnin = 1000, 
  n.thin = 10
)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 40
   Unobserved stochastic nodes: 19
   Total graph size: 208

Initializing model

# View summary of the model fit
print(jags_fit)

Inference for Bugs model at "./codigoJAGS/pilots_adjusted.jags", fit using jags,
 3 chains, each with 5000 iterations (first 1000 discarded), n.thin = 10
 n.sims = 1200 iterations saved. Running time = 0.595 secs
         mu.vect sd.vect    2.5%     25%    50%    75%  97.5%  Rhat n.eff
d.adj[1]  -0.097   0.089  -0.273  -0.156 -0.096 -0.042  0.075 1.000  1200
d.adj[2]  -0.283   0.097  -0.474  -0.341 -0.283 -0.220 -0.083 1.004   530
d.adj[3]   0.001   0.090  -0.183  -0.059  0.000  0.060  0.183 1.000  1200
d.adj[4]  -0.219   0.090  -0.393  -0.279 -0.219 -0.160 -0.042 1.002   820
d.adj[5]  -0.018   0.088  -0.205  -0.081 -0.016  0.042  0.143 1.001  1200
d.adj[6]   0.486   0.095   0.291   0.427  0.488  0.549  0.670 1.000  1200
d.adj[7]  -0.308   0.094  -0.497  -0.369 -0.309 -0.249 -0.114 1.005   450
d.adj[8]   0.438   0.094   0.250   0.375  0.438  0.499  0.626 1.005   990
g.adj[1]  -0.012   0.042  -0.109  -0.029 -0.005  0.008  0.069 1.004   510
g.adj[2]  -0.007   0.037  -0.089  -0.024 -0.002  0.010  0.072 1.001  1200
g.adj[3]   0.002   0.039  -0.084  -0.014  0.001  0.019  0.088 1.002   750
g.adj[4]  -0.008   0.042  -0.109  -0.027 -0.002  0.010  0.075 1.004   640
g.adj[5]   0.026   0.045  -0.041  -0.001  0.012  0.049  0.141 1.001  1200
mu.adj     0.441   0.037   0.368   0.416  0.440  0.465  0.515 1.002  1200
mu.d       1.646   1.761  -1.382   0.368  1.422  3.227  4.642 2.970     4
mu.g      -0.358   2.109  -3.578  -2.573 -0.434  1.355  3.324 5.597     3
sigma.d    0.395   0.150   0.206   0.297  0.364  0.451  0.770 1.000  1200
sigma.g    0.060   0.059   0.001   0.019  0.044  0.080  0.222 1.009   510
sigma.y    0.228   0.030   0.177   0.206  0.226  0.247  0.293 1.001  1200
deviance  -6.660   5.375 -14.713 -10.631 -7.553 -3.707  5.615 1.000  1200

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule: pV = var(deviance)/2)
pV = 14.5 and DIC = 7.8
DIC is an estimate of expected predictive error (lower deviance is better).