1  Pensamiento Bayesiano

1.1 Introducción al Método Científico y la Estadística Bayesiana

El método científico es la base de todo proceso de aprendizaje y toma de decisiones. En este contexto, la estadística bayesiana se presenta como una herramienta poderosa para incorporar y actualizar información de forma cuantitativa. A continuación, se describen los pasos fundamentales que integran este enfoque:

• Definición del Problema:
  El primer paso consiste en identificar claramente la pregunta o el problema a resolver.

• Evaluación de Información Previa:

  • Revisar los datos y conocimientos existentes.
    
  • Si la información es suficiente, se extraen conclusiones y se toman decisiones.
    
  • Si no lo es, se planifica la obtención de nuevos datos.

• Obtención de Nueva Información:
  Diseñar y ejecutar experimentos o estudios que permitan recolectar datos adicionales necesarios para abordar el problema.

• Actualización del Conocimiento:
  Integrar la nueva información con la que ya se tiene, repitiendo el proceso de evaluación de forma iterativa para perfeccionar la comprensión del fenómeno.

• Aplicación de la Estadística Bayesiana:
  Este enfoque es especialmente útil en las etapas de evaluación y actualización, ya que permite incorporar evidencia de forma cuantitativa y ajustar las conclusiones conforme se dispone de nueva información.

1.2 Ilustración del Método Científico

El siguiente diagrama de flujo resume el proceso del método científico:

flowchart TD
  A[Definir el problema] --> B[Evaluar informacion previa]
  B --> C{"Informacion suficiente?"}
  C -- "Si" --> D[Extraer conclusiones y tomar decisiones]
  C -- "No" --> E[Disenar estudio/experimento]
  E --> F[Ejecutar estudio/experimento]
  F --> G[Actualizar conocimiento]
  G --> B

Este diagrama ilustra cómo, a partir de la definición del problema, se evalúa la información disponible y, en función de su suficiencia, se decide si es necesario recolectar más datos. Luego, los nuevos datos se integran al conocimiento previo, reiniciando el ciclo para mejorar continuamente la toma de decisiones.

1.3 Breve Historia de la Estadística Bayesiana

La evolución de la estadística bayesiana está profundamente ligada a eventos históricos y avances metodológicos:

• El Gran Incendio de Londres (1666):
  Este catastrófico suceso impulsó el desarrollo de los seguros, lo que generó la necesidad de evaluar riesgos de manera probabilística.

• Contribuciones de Thomas Bayes (1702-1761):
  Como ministro y matemático, Bayes desarrolló un método para abordar problemas de probabilidad. Su trabajo, publicado póstumamente en 1764, sentó las bases del enfoque bayesiano.

• Recepción y Evolución del Método:
  Inicialmente, figuras como Pierre-Simon Laplace aceptaron y ampliaron el método, aunque posteriormente pensadores como George Boole lo cuestionaron, lo que llevó a su constante evolución.

• Desarrollo Reciente:
  Hasta la década de 1990, la aplicación de métodos bayesianos estaba limitada por las capacidades computacionales. Sin embargo, los avances en el poder de cómputo y el desarrollo de nuevos algoritmos han permitido su aplicación en áreas complejas como la astrofísica, la meteorología, la salud y la conducción autónoma.

1.4 Los Tres Pasos del Análisis de Datos Bayesiano

El análisis bayesiano se estructura en tres pasos clave que permiten transformar la información en conocimiento útil:

1. Configuración del Modelo de Probabilidad Completo:
   Se establece una distribución conjunta que abarca todas las variables involucradas (observables y no observables), asegurando la coherencia del modelo con el conocimiento previo y el proceso de recolección de datos.

2. Condicionamiento sobre los Datos Observados:
   Se calcula la distribución posterior, la cual representa la probabilidad condicional de las variables de interés no observadas, dada la evidencia recopilada. Este paso es fundamental para actualizar nuestras creencias sobre el modelo.

3. Evaluación del Ajuste del Modelo y Análisis de la Distribución Posterior:
   Se verifica la capacidad del modelo para ajustarse a los datos observados y se evalúa la razonabilidad de las conclusiones derivadas. Asimismo, se analiza la sensibilidad de los resultados frente a las suposiciones iniciales, lo que permite modificar o ampliar el modelo según sea necesario.

1.5 Ventajas y Consideraciones del Enfoque Bayesiano

El enfoque bayesiano presenta diversas ventajas y algunos desafíos que es importante considerar:

• Interpretación Directa de los Intervalos:
  Los intervalos bayesianos se interpretan como la probabilidad de que contengan el valor desconocido, lo que resulta más intuitivo que la interpretación frequentista de los intervalos de confianza.

• Flexibilidad para Modelos Complejos:
  La capacidad de incorporar múltiples parámetros y estructuras multinivel permite aplicar el enfoque bayesiano a problemas muy complejos.

• Desafíos en la Especificación del Modelo:
  La construcción inicial del modelo puede ser complicada. Sin embargo, los avances en técnicas computacionales y en métodos de evaluación del ajuste han facilitado este proceso, permitiendo explorar y ajustar las suposiciones a priori de manera más sistemática.

1.6 Notación General para la Inferencia Estadística

La inferencia estadística se encarga de extraer conclusiones a partir de datos numéricos sobre cantidades que no se observan directamente. Por ejemplo, en un ensayo clínico se puede comparar la probabilidad de supervivencia a cinco años entre diferentes tratamientos; estas probabilidades se estiman a partir de una muestra, ya que no es posible ni ético experimentar en toda la población o exponer a un mismo paciente a ambos tratamientos.

1.6.1 Tipos de Estimandos y Notación

Se distinguen dos tipos de estimandos:

• Cantidades potencialmente observables:
  Por ejemplo, futuros resultados de un proceso o el resultado de un paciente bajo el tratamiento que no recibió.

• Parámetros no observables:
  Aquellos que gobiernan el proceso hipotético que genera los datos, como los coeficientes de regresión.

La notación general es la siguiente:

• \(\theta\): Vector de parámetros o cantidades no observables de interés (por ejemplo, probabilidades de supervivencia).

• \(y\): Datos observados (pueden ser escalares, vectores o matrices, como los resultados de pacientes en un estudio).

• \(\tilde{y}\): Cantidades desconocidas, pero potencialmente observables (por ejemplo, resultados futuros o contrafactuales).

1.6.2 Unidades y Variables Observacionales

En muchos estudios se recolectan datos de \(n\) unidades. Se representan de la siguiente forma: \[ y = (y_1, y_2, \ldots, y_n) \] Cada \(y_i\) puede ser un escalar o un vector, y si se miden varias variables por unidad, el conjunto completo de datos se organiza en una matriz (usualmente con \(n\) filas). Los valores de \(y\) se consideran aleatorios, ya que pueden variar debido al proceso de muestreo y a la variación natural de la población.

1.6.3 Intercambiabilidad

Un supuesto fundamental en la inferencia estadística es la intercambiabilidad. Se asume que la densidad conjunta \[ p(y_1, y_2, \ldots, y_n) \] es invariante a cualquier permutación de los índices, lo que implica que, en ausencia de información adicional, los datos se pueden modelar como independientes e idénticamente distribuidos (iid) dado algún parámetro desconocido \(\theta\).

1.6.4 Variables Explicativas

Además de los resultados \(y\), es común recopilar variables que, aunque no se modelan como aleatorias, influyen en los resultados. Estas son las variables explicativas o covariables, denotadas por \(x\).
El conjunto completo de estas variables se representa como una matriz \(X\) con \(n\) filas y \(k\) columnas, donde \(k\) es el número de covariables.
Al incorporar \(X\) en el análisis, se puede asumir que la distribución de \(y\), condicional a \(x\), es la misma para todas las unidades que tengan el mismo valor en \(x\).

1.6.5 Modelado Jerárquico

En estudios que recogen información en distintos niveles (por ejemplo, pacientes dentro de diferentes ciudades), se emplean modelos jerárquicos o multinivel.
En estos modelos, se puede asumir intercambiabilidad a cada nivel:

• Los pacientes dentro de cada ciudad se consideran intercambiables.

• Además, los resultados entre ciudades también pueden ser tratados como intercambiables si no se dispone de otra información relevante a nivel de ciudad.

Este marco notacional y conceptual es fundamental para entender cómo se relacionan los datos observados, las cantidades desconocidas y las variables explicativas en un modelo estadístico, proporcionando una base sólida para la inferencia bayesiana.

1.7 Inferencia Bayesiana

La inferencia bayesiana se fundamenta en expresar conclusiones sobre un parámetro desconocido, \(\theta\), o sobre datos no observados, \(\tilde{y}\), en forma de declaraciones de probabilidad. Dichas probabilidades se condicionan en los datos observados, \(y\), y en los valores conocidos de cualquier covariable, \(x\). Este enfoque se diferencia del tradicional método frequentista, ya que se basa en la actualización directa de nuestras creencias a partir de la evidencia, en lugar de evaluar procedimientos repetitivos.

1.8 Notación de Probabilidad

• Función condicional:
  Se utiliza la notación \(p(\cdot \mid \cdot)\) para denotar funciones de densidad condicional (aplicable tanto a variables continuas como discretas).
  
• Distribución a priori:
  \(p(\theta)\) representa la distribución marginal o a priori del parámetro \(\theta\).
  
• Distribución de muestreo o verosimilitud:
  \(p(y \mid \theta)\) es la función que describe la probabilidad de observar los datos \(y\), dado un valor de \(\theta\).
  
• Ejemplo de notación estándar:
  Si \(\theta\) tiene una distribución normal con media \(\mu\) y varianza \(\sigma^2\), se escribe: \[ \theta \sim \mathrm{N}(\mu, \sigma^2) \quad \text{o} \quad p(\theta)=\mathrm{N}(\theta \mid \mu, \sigma^2). \]

En ocasiones se emplea \(\operatorname{Pr}(\cdot)\) para enfatizar la probabilidad de eventos específicos, especialmente cuando se trabaja con espacios muestrales suprimidos en la notación.

1.9 Regla de Bayes

Para realizar inferencias sobre \(\theta\) a partir de los datos observados, se parte de un modelo conjunto para \(\theta\) y \(y\), expresado como: \[ p(\theta, y) = p(\theta) \, p(y \mid \theta). \] Aplicando la regla de Bayes se obtiene la densidad posterior: \[ p(\theta \mid y) = \frac{p(\theta) \, p(y \mid \theta)}{p(y)}, \] donde \(p(y)\), la probabilidad marginal de los datos, se calcula sumando o integrando sobre todos los valores de \(\theta\). De forma equivalente, se puede escribir: \[ p(\theta \mid y) \propto p(\theta) \, p(y \mid \theta). \]

1.10 Predicción

Para predecir un dato observable futuro, \(\tilde{y}\), se utiliza la distribución predictiva posterior: \[ p(\tilde{y} \mid y) = \int p(\tilde{y} \mid \theta) \, p(\theta \mid y) \, d\theta. \] Esta fórmula representa un promedio ponderado de las predicciones condicionales \(p(\tilde{y} \mid \theta)\), sobre la distribución posterior de \(\theta\).

1.11 Función de Verosimilitud

En la inferencia bayesiana, el papel de los datos se resume en la función de verosimilitud \(p(y \mid \theta)\), que, para un conjunto fijo de datos, se considera una función de \(\theta\). Según el principio de verosimilitud, dos modelos que generen la misma función de verosimilitud conducirán a las mismas inferencias sobre \(\theta\).

1.12 Verosimilitud y Razones de Probabilidad

La comparación entre dos valores de \(\theta\), digamos \(\theta_1\) y \(\theta_2\), se puede expresar mediante la razón de probabilidades posterior: \[ \frac{p(\theta_1 \mid y)}{p(\theta_2 \mid y)} = \frac{p(\theta_1)}{p(\theta_2)} \, \frac{p(y \mid \theta_1)}{p(y \mid \theta_2)}. \] Esto muestra que las probabilidades posteriores son el producto de las probabilidades a priori (la razón de probabilidades) y el cociente de verosimilitud, lo que simplifica la interpretación comparativa entre diferentes valores de \(\theta\).

1.13 Ejemplos Discretos en Inferencia Bayesiana

En esta sección se ilustran dos ejemplos discretos en los cuales el objetivo inmediato es inferir sobre una cantidad específica en lugar de estimar un parámetro que describe una población completa. Estos ejemplos permiten ver de manera directa las probabilidades a priori, la verosimilitud y la probabilidad posterior.

---

1.13.1 Inferencia sobre el Estado Genético

Contexto:
Se analiza la probabilidad de que una mujer sea portadora de la hemofilia, una enfermedad de herencia recesiva ligada al cromosoma X.

Situación:
- Los hombres tienen un cromosoma X y uno Y, mientras que las mujeres tienen dos cromosomas X.
- La hemofilia afecta a los hombres que heredan el gen defectuoso y, en mujeres, solo se manifiesta si heredan ambos genes defectuosos (lo cual es raro).

Información previa (a priori):
- Una mujer tiene un hermano afectado, lo que implica que su madre es portadora (un gen “bueno” y uno “defectuoso”).
- Su padre no está afectado, por lo tanto, la mujer tiene una probabilidad del 50% de ser portadora: \[ \operatorname{Pr}(\theta=1)=\operatorname{Pr}(\theta=0)=0.5, \] donde \(\theta=1\) indica que es portadora y \(\theta=0\) lo contrario.

Modelo de Datos y Verosimilitud:
- La mujer tiene dos hijos varones, ninguno de los cuales está afectado.
- Si ella es portadora, cada hijo tiene un 50% de heredar el gen defectuoso, por lo que la probabilidad de que ambos sean sanos es: \[ \operatorname{Pr}(y_1=0, y_2=0 \mid \theta=1)=0.5 \times 0.5 = 0.25. \] - Si no es portadora, la probabilidad de que ambos hijos sean sanos es casi 1: \[ \operatorname{Pr}(y_1=0, y_2=0 \mid \theta=0)=1 \times 1 = 1. \]

Cálculo de la Probabilidad Posterior:
Aplicando la regla de Bayes, se obtiene: \[ \operatorname{Pr}(\theta=1 \mid y) = \frac{(0.25)(0.5)}{(0.25)(0.5) + (1.0)(0.5)} = \frac{0.125}{0.625} = 0.20. \]

Actualización con Más Datos:
Si la mujer tiene un tercer hijo varón y este también es sano, se usa la distribución posterior anterior como a priori para actualizar la inferencia: \[ \operatorname{Pr}(\theta=1 \mid y_1, y_2, y_3) = \frac{(0.5)(0.20)}{(0.5)(0.20) + (1)(0.80)} \approx 0.111. \]

En cambio, si el tercer hijo estuviera afectado, la probabilidad posterior de que la mujer sea portadora se elevaría hasta 1 (ignorando la posibilidad de mutación).

---

1.13.2 Corrección Ortográfica

Contexto:
Se aborda la clasificación de palabras con el objetivo de corregir errores tipográficos. Por ejemplo, al escribir “radom”, se quiere determinar si se trató de un error al teclear “random” o “radon”, o si realmente se pretendía escribir “radom”.

Modelo del Problema:
- Dato observado (\(y\)): La palabra “radom”.
- Parámetro desconocido (\(\theta\)): La palabra que se pretendía escribir (posibles valores: “random”, “radon” o “radom”).

La regla de Bayes se expresa como: \[ \operatorname{Pr}(\theta \mid y=\text{'radom'}) \propto p(\theta) \, \operatorname{Pr}(y=\text{'radom'} \mid \theta). \]

Distribución a Priori:
- Las probabilidades a priori de cada palabra pueden basarse en su frecuencia en un corpus de texto. Por ejemplo, se pueden obtener valores relativos de ocurrencia para “random”, “radon” y “radom” (estos valores pueden ser ajustados y renormalizados según el contexto).

Verosimilitud:
- Se utilizan modelos de errores tipográficos para estimar las probabilidades condicionales:

\(\theta\)	\(\operatorname{Pr}(\text{'radom'} \mid \theta)\)
random	0.00193
radon	0.000143
radom	0.975

Estos valores indican, por ejemplo, que existe un 97% de probabilidad de que se escriba “radom” correctamente, mientras que las probabilidades de que “radom” resulte de un error al escribir “random” o “radon” son muy bajas.

Distribución Posterior:
Multiplicando las probabilidades a priori por la verosimilitud y renormalizando se obtienen:

\(\theta\)	\(p(\theta) \, p(\text{'radom'} \mid \theta)\)	Probabilidad Posterior
random	\(1.47 \times 10^{-7}\)	0.325
radon	\(8.65 \times 10^{-10}\)	0.002
radom	\(3.04 \times 10^{-7}\)	0.673

Así, de acuerdo con el modelo, la palabra “radom” es más probable que sea correcta (67.3%) que un error tipográfico de “random” (32.5%), y es muy poco probable que se trate de “radon” (0.2%).

Decisión y Mejora del Modelo:
- Decisión: Con estos resultados, se podría aceptar “radom” como correcta, o bien cuestionar el modelo si se cree que el contexto sugiere que debería ser “random”.
- Mejora: Se puede incorporar información contextual (por ejemplo, si el documento es un libro de estadística, la palabra “random” es más frecuente) mediante: \[ p(\theta \mid x, y) \propto p(\theta \mid x) \, p(y \mid \theta, x), \] donde \(x\) representa la información contextual.

En la práctica, el reto consiste en establecer modelos adecuados para estimar todas estas probabilidades a partir de datos, pero la regla de Bayes ofrece un mecanismo claro para integrar la información previa con la evidencia observada.

1.14 Pensamiento Bayesiano (Computacional)

1.14.1 Hábitos de sueño

Se desea investigar los hábitos de sueño de los estudiantes universitarios en Estados Unidos, específicamente, determinar qué proporción, denotada por \(p\), duerme al menos ocho horas durante una noche típica entre semana. El valor de \(p\) es desconocido y, en el enfoque bayesiano, las creencias previas acerca de este parámetro se representan mediante una distribución a priori, la cual refleja opiniones subjetivas sobre los valores plausibles de \(p\).

1.14.1.1 Investigación Previa y Construcción de la A Priori

Antes de recolectar datos, la investigadora realiza una investigación preliminar:

• En el artículo “College Students Don’t Get Enough Sleep” se indica que la mayoría de los estudiantes duerme aproximadamente seis horas diarias.
• En otro artículo, basado en una muestra de 100 estudiantes, se reporta que cerca del 70% duerme entre cinco y seis horas, un 28% duerme entre siete y ocho horas, y solo un 2% duerme nueve horas (valor saludable).

Con esta información, la investigadora infiere que es probable que \(p\) (la proporción de estudiantes que duermen al menos ocho horas) sea menor a 0.5. Tras reflexionar, su mejor estimación es \(p \approx 0.3\), aunque es plausible que el valor de \(p\) esté en el intervalo de 0 a 0.5.

1.14.1.2 Recolección de Datos y Modelo de Likelihood

Se toma una muestra aleatoria de 27 estudiantes, de los cuales 11 reportan haber dormido al menos ocho horas la noche anterior. Si definimos un “éxito” como dormir al menos ocho horas y \(s\) y \(f\) como el número de éxitos y fracasos, respectivamente, la función de verosimilitud se expresa como: \[ L(p) \propto p^{s}(1-p)^{f}, \quad 0 < p < 1. \]

1.14.1.3 Actualización de Creencias: Distribución Posterior

Aplicando la regla de Bayes, la distribución posterior de \(p\) se obtiene multiplicando la distribución a priori \(g(p)\) por la verosimilitud: \[ g(p \mid \text{datos}) \propto g(p) \, L(p). \] Esta posterior se utilizará para estimar la proporción \(p\) a partir de la información combinada de la investigación previa y los datos observados.

1.14.1.4 Predicción

Además, la investigadora está interesada en predecir el número de estudiantes que dormirán al menos ocho horas en una nueva muestra de 20 estudiantes, utilizando el mismo enfoque bayesiano.

1.14.2 Uso de una Priori Discreta para la Proporción

Una forma sencilla de evaluar una distribución a priori para la proporción ( p ) es listar valores plausibles y asignarles pesos. En nuestro ejemplo, se consideran los siguientes valores para ( p ): \[ 0.05,\; 0.15,\; 0.25,\; 0.35,\; 0.45,\; 0.55,\; 0.65,\; 0.75,\; 0.85,\; 0.95 \]

La investigadora asigna a estos valores los pesos: \[ 1,\; 5.2,\; 8,\; 7.2,\; 4.6,\; 2.1,\; 0.7,\; 0.1,\; 0,\; 0 \]

Dividiendo cada peso por la suma total se obtienen las probabilidades a priori. En R, se define el vector p con los valores de proporción y prior con los pesos normalizados, y se grafica la distribución a priori:

p = seq(0.05, 0.95, by = 0.1)
prior = c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior = prior / sum(prior)
plot(p, prior, type = "h", ylab = "Prior Probability")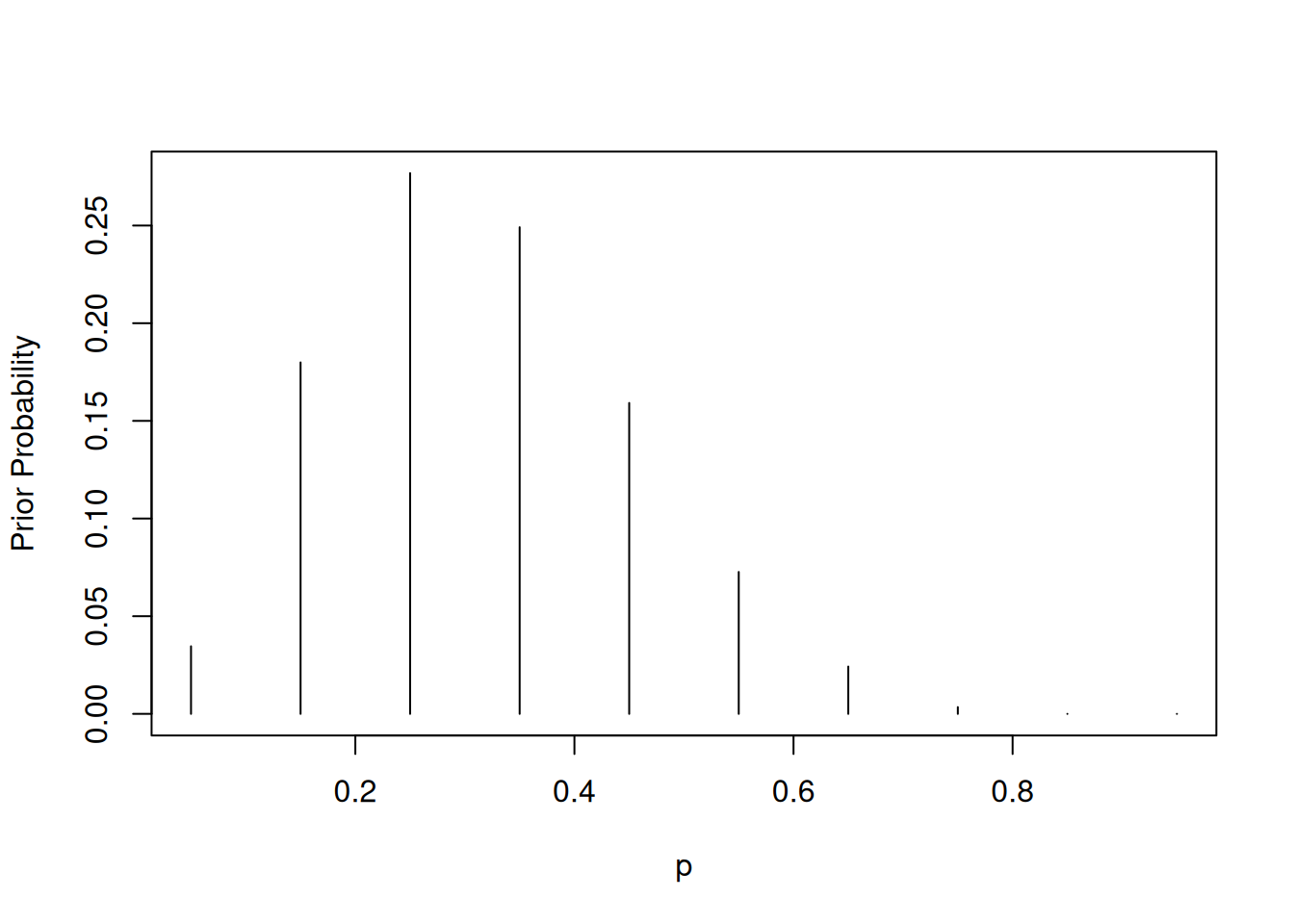

1.14.2.1 Incorporación de Datos y Función de Verosimilitud

En el ejemplo, se observó que 11 de 27 estudiantes duermen lo suficiente, es decir, $ s = 11 $ éxitos y $ f = 16 $ fracasos. La función de verosimilitud es: \[ L(p) \propto p^{11} (1-p)^{16}, \quad 0 < p < 1, \] lo que equivale a una densidad beta con parámetros $ s+1 = 12 $ y $ f+1 = 17 $.

La función pdisc del paquete LearnBayes calcula las probabilidades posteriores. Para usarla, se le suministra el vector de valores $ p $, el vector de probabilidades a priori prior y un vector de datos data con $ s $ y $ f $:

library(LearnBayes)
data = c(11, 16)
post = pdisc(p, prior, data)
round(cbind(p, prior, post), 2)

         p prior post
 [1,] 0.05  0.03 0.00
 [2,] 0.15  0.18 0.00
 [3,] 0.25  0.28 0.13
 [4,] 0.35  0.25 0.48
 [5,] 0.45  0.16 0.33
 [6,] 0.55  0.07 0.06
 [7,] 0.65  0.02 0.00
 [8,] 0.75  0.00 0.00
 [9,] 0.85  0.00 0.00
[10,] 0.95  0.00 0.00

La salida muestra una tabla con las probabilidades a priori y las posteriores. Se observa que la mayor parte de la probabilidad posterior se concentra en $ p = 0.35 $ y $ p = 0.45 $. Si se combinan las probabilidades de los tres valores más probables (0.25, 0.35 y 0.45), la probabilidad de que $ p $ pertenezca al conjunto \(\{0.25, 0.35, 0.45\}\) es aproximadamente 0.940.

1.14.2.2 Gráficos Comparativos

Para visualizar las distribuciones a priori y posterior, se utiliza el paquete lattice:

library(lattice)
PRIOR = data.frame(Type = "prior", P = p, Probability = prior)
POST = data.frame(Type = "posterior", P = p, Probability = post)
data_plot = rbind(PRIOR, POST)
xyplot(Probability ~ P | Type, data = data_plot, layout = c(1, 2),
       type = "h", lwd = 3, col = "black")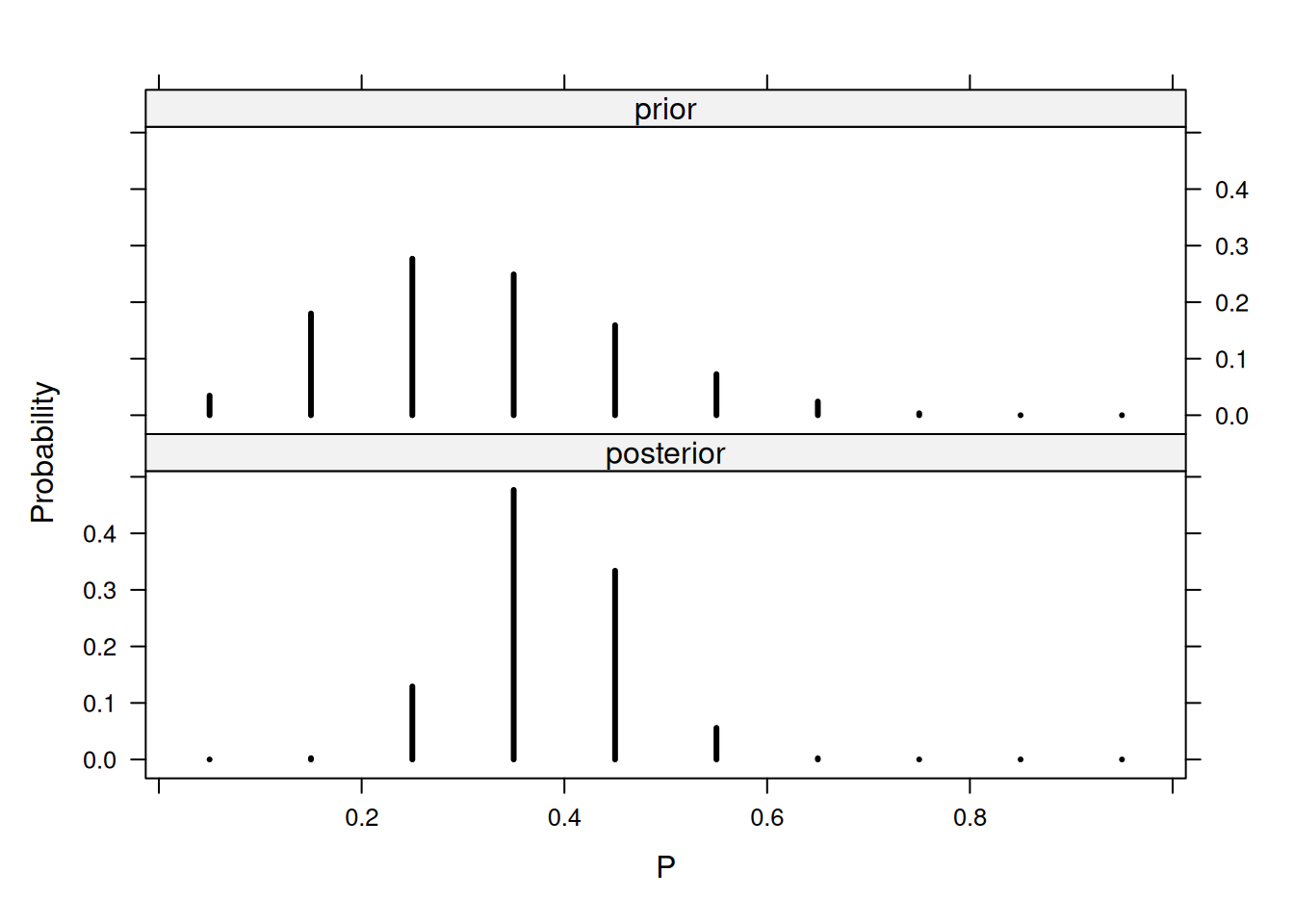

Este gráfico comparativo ilustra cómo la evidencia de los datos concentra la probabilidad en los valores $ p = 0.35 $ y $ p = 0.45 $.

1.14.3 Uso de una Prior Beta

Dado que la proporción \(p\) es un parámetro continuo (entre 0 y 1), una alternativa para representar las creencias previas es utilizar una densidad continua \(g(p)\) basada en la familia beta.

1.14.3.1 Planteamiento de la Información a Priori

Supongamos que la investigadora cree que:

• La proporción es igualmente probable que sea menor o mayor que \(p = 0.3\) (es decir, la mediana es 0.3).
• Está 90% segura de que \(p\) es menor que 0.5.

La familia beta tiene una función núcleo: \[ g(p) \propto p^{a-1}(1-p)^{b-1}, \quad 0<p<1, \] donde los hiperparámetros \(a\) y \(b\) se eligen para reflejar las creencias previas. La media de una beta es \[ m = \frac{a}{a+b}, \] y su varianza es \[ v = \frac{m(1-m)}{a+b+1}. \]

Es más sencillo determinar \(a\) y \(b\) mediante afirmaciones sobre los percentiles de la distribución. Por ejemplo, utilizando la función beta.select del paquete LearnBayes, se pueden especificar:

• La mediana (\(p=0.3\)) y
• El percentil 90 (\(p=0.5\)).

El código en R sería:

quantile1 = list(p = 0.5, x = 0.3)
quantile2 = list(p = 0.9, x = 0.5)
beta.select(quantile1, quantile2)

[1] 3.26 7.19

Esto indica que la información previa se ajusta a una distribución beta con \(a \approx 3.26\) y \(b \approx 7.19\).

1.14.3.2 Combinación con la Verosimilitud y la Distribución Posterior

Si se recogen datos (por ejemplo, \(s\) éxitos y \(f\) fracasos), la función de verosimilitud es: \[ L(p) \propto p^{s}(1-p)^{f}. \]

Aplicando la regla de Bayes, la distribución posterior es: \[ g(p \mid \text{datos}) \propto p^{a+s-1}(1-p)^{b+f-1}, \quad 0<p<1, \] es decir, la posterior es también una beta con parámetros actualizados \(a+s\) y \(b+f\). Este es un ejemplo de análisis conjugado.

1.14.3.3 Visualización y Resumen en R

Dado que la priori, la verosimilitud y la posterior pertenecen a la familia beta, se pueden usar funciones como dbeta para graficarlas. Por ejemplo:

a = 3.26
b = 7.19
s = 11  # número de éxitos
f = 16  # número de fracasos

# Graficar la posterior, la verosimilitud (como beta(s+1, f+1)) y la priori
curve(dbeta(x, a+s, b+f), from = 0, to = 1,
      xlab = "p", ylab = "Densidad", lty = 1, lwd = 4)
curve(dbeta(x, s+1, f+1), add = TRUE, lty = 2, lwd = 4)
curve(dbeta(x, a, b), add = TRUE, lty = 3, lwd = 4)
legend(0.7, 4, c("Prior", "Verosimilitud", "Posterior"),
       lty = c(3, 2, 1), lwd = c(3, 3, 3))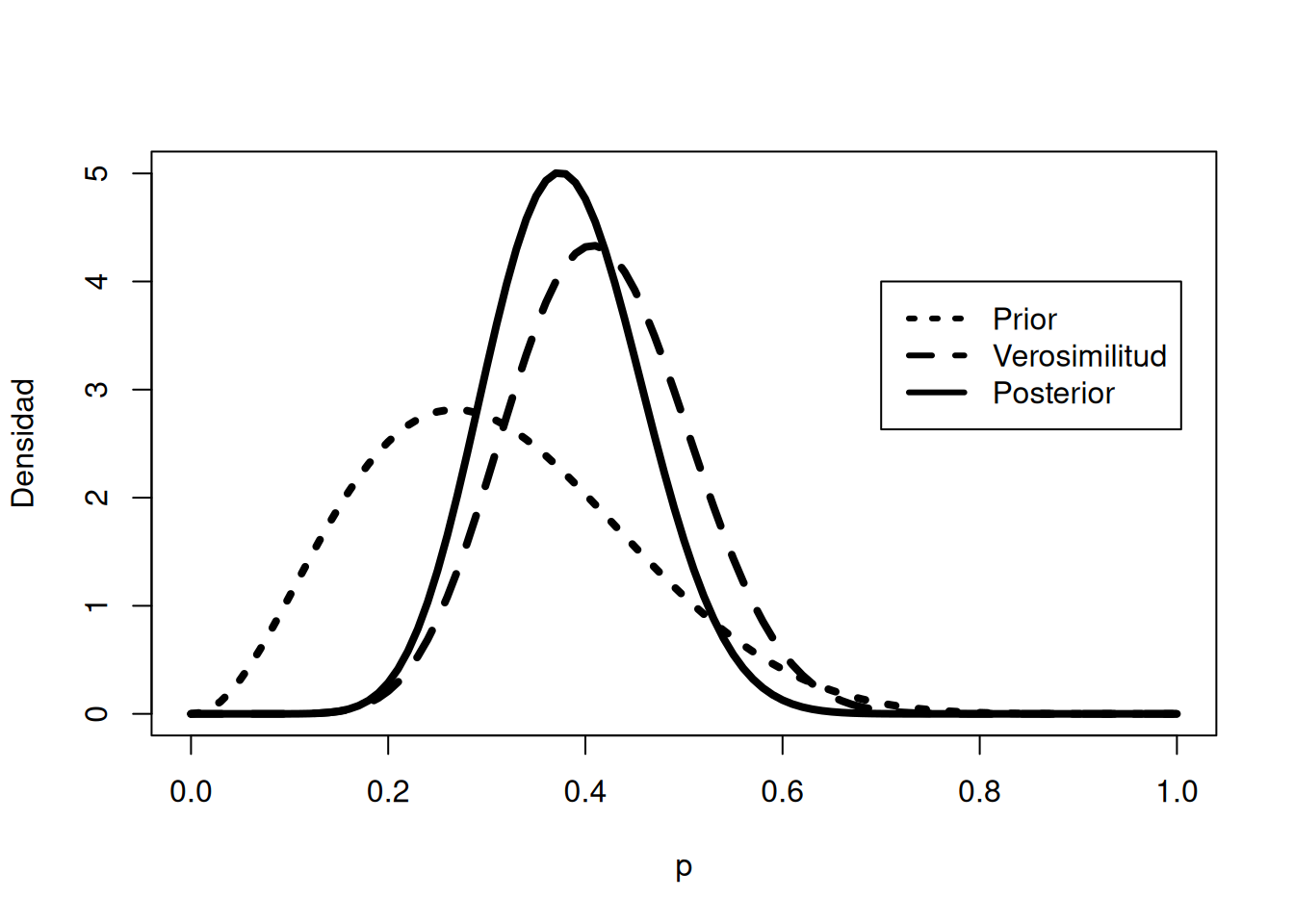

1.14.3.4 Resúmenes del Posterior

Para calcular probabilidades y construir intervalos de credibilidad se utilizan funciones como pbeta y qbeta:

• Probabilidad de que \(p \geq 0.5\):

1 - pbeta(0.5, a + s, b + f)

[1] 0.0690226

La salida puede ser, por ejemplo, aproximadamente 0.068, indicando que es poco probable que más de la mitad de los estudiantes sean “heavy sleepers”.

• Intervalo de Credibilidad del 90% para \(p\):

qbeta(c(0.05, 0.95), a + s, b + f)

Esto podría dar un intervalo, por ejemplo, \((0.256, 0.513)\).

1.14.3.5 Resumen mediante Simulación

Alternativamente, se pueden simular valores de la posterior usando rbeta:

ps = rbeta(1000, a+s, b+f)
hist(ps, xlab = "p", main = "")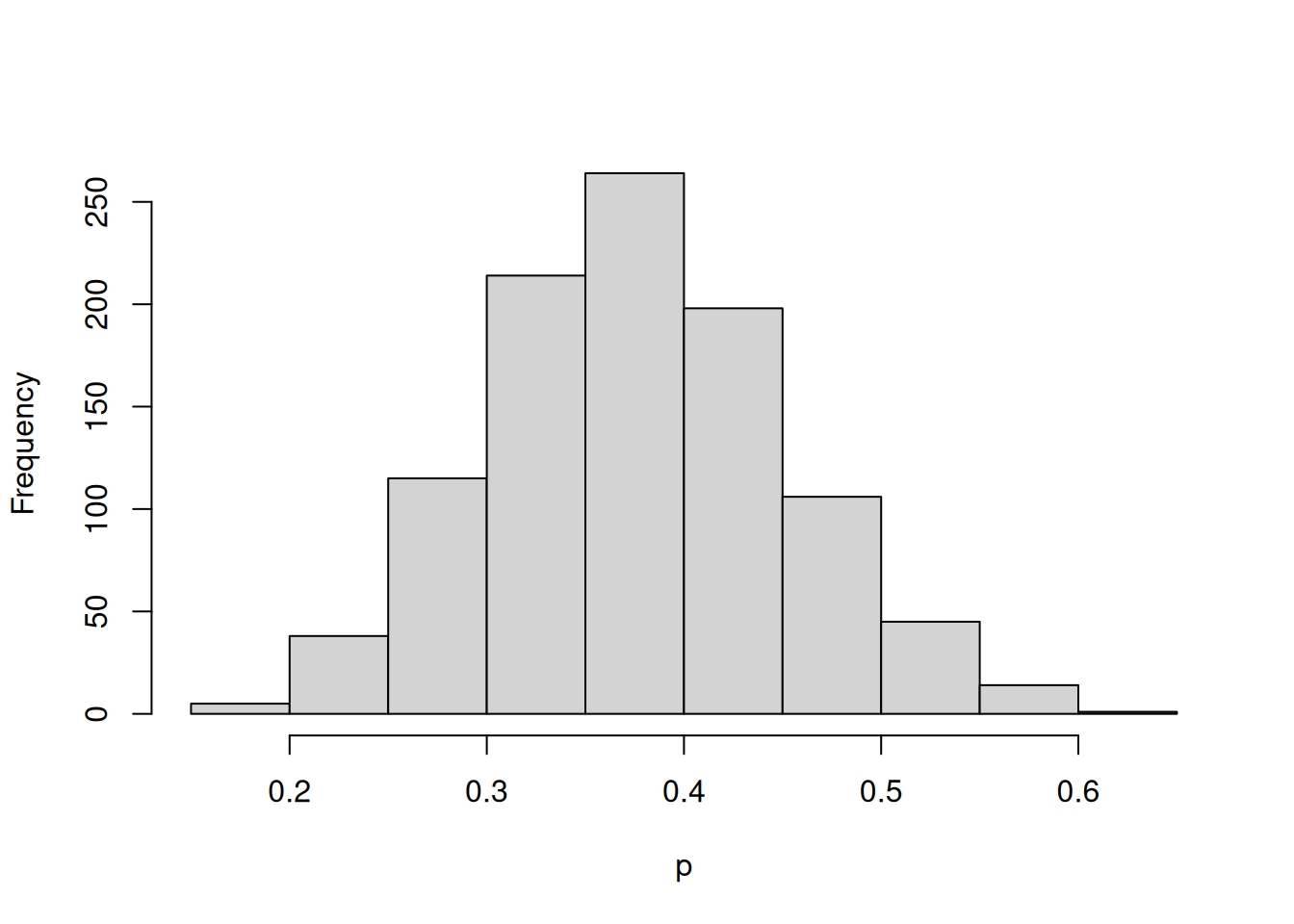

La probabilidad de que \(p \geq 0.5\) se puede estimar como:

sum(ps >= 0.5) / 1000

[1] 0.067

Y el intervalo de credibilidad del 90% se estima usando:

quantile(ps, c(0.05, 0.95))

       5%       95% 
0.2586332 0.5115310 

Los resultados obtenidos por simulación son aproximadamente iguales a los calculados exactamente con las funciones beta.

1.14.4 Uso de una Prior Tipo Histograma

Aunque el uso de una prior beta ofrece ventajas computacionales, es sencillo realizar cálculos posteriores con cualquier elección de prior. A continuación se describe un método “brute-force” para resumir los cálculos de la posterior a partir de una densidad a priori arbitraria \(g(p)\):

1. Definir una rejilla de valores para \(p\):
   Seleccionar una secuencia de valores en el intervalo que cubre la densidad posterior.

2. Calcular el producto de la verosimilitud y la a priori:
   En cada punto de la rejilla, se evalúa \(L(p) \times g(p)\).

3. Normalizar:
   Dividir cada producto por la suma total de los productos para aproximar la densidad posterior mediante una distribución de probabilidad discreta en la rejilla.

4. Simulación:
   Utilizar la función sample en R para tomar una muestra aleatoria (con reemplazo) de esta distribución discreta.
   Los valores simulados aproximan una muestra de la distribución posterior.

1.14.4.1 Ejemplo con una Prior Tipo Histograma

Supongamos que la investigadora prefiere expresar sus creencias sobre la proporción de “heavy sleepers” dividiendo el rango de \(p\) en diez subintervalos \((0,0.1),\;(0.1,0.2),\;\ldots,\;(0.9,1)\) y asignando a cada uno un peso. En nuestro ejemplo, se asignan los siguientes pesos:

\[ 1,\; 5.2,\; 8,\; 7.2,\; 4.6,\; 2.1,\; 0.7,\; 0.1,\; 0,\; 0. \]

En R, representamos este prior tipo histograma de la siguiente forma:

# Definir los puntos medios y los pesos de la prior
midpt = seq(0.05, 0.95, by = 0.1)
prior = c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior = prior / sum(prior)  # Normalizar los pesos a probabilidades

# Graficar la densidad a priori utilizando la función histprior del paquete LearnBayes
curve(histprior(x, midpt, prior), from = 0, to = 1,
      ylab = "Prior density", ylim = c(0, 0.3))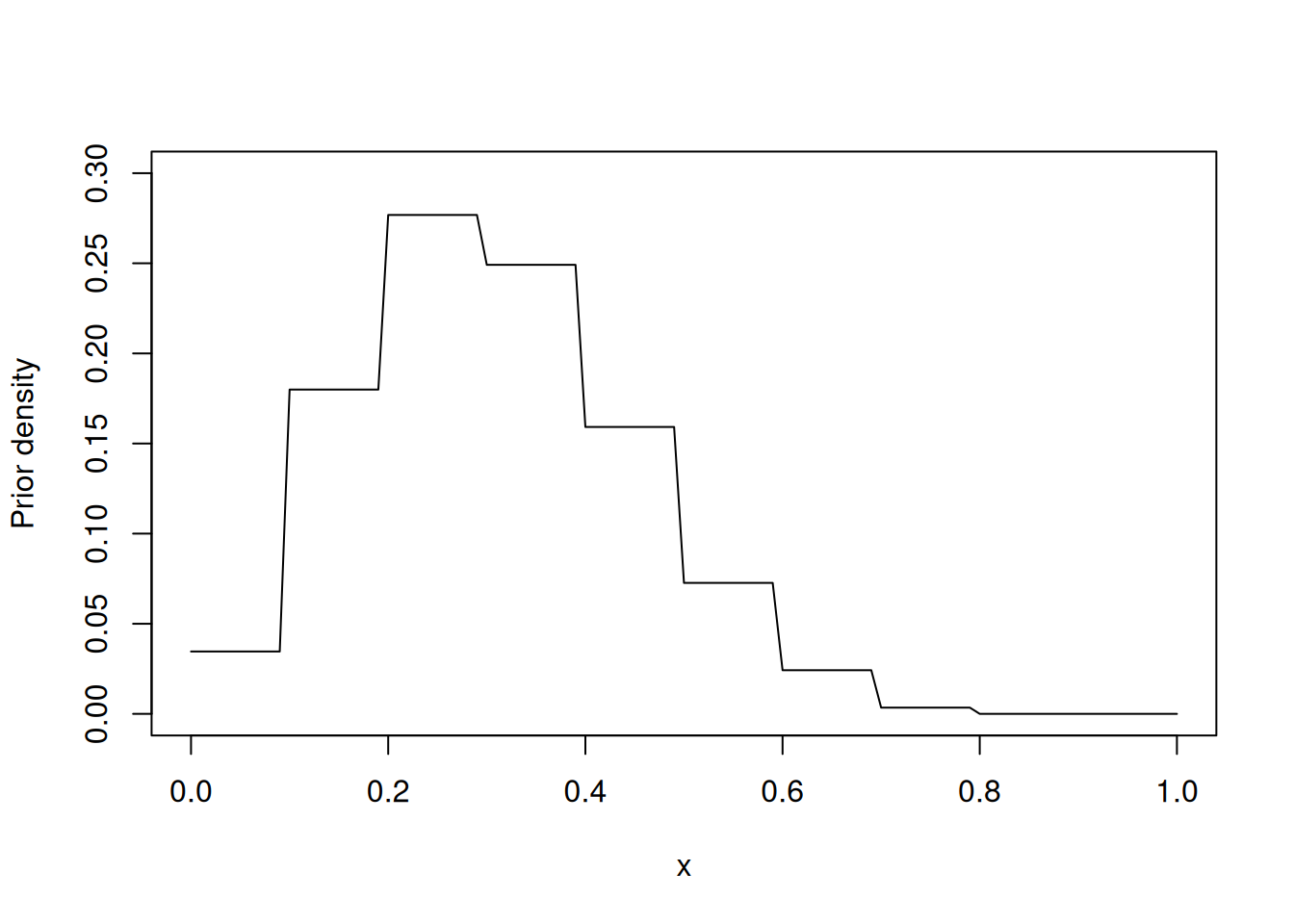

A continuación, se obtiene la densidad posterior multiplicando la prior por la función de verosimilitud. Recordemos que la verosimilitud para una distribución binomial se expresa como una densidad beta con parámetros \(s+1\) y \(f+1\):

# Graficar la densidad posterior
curve(histprior(x, midpt, prior) * dbeta(x, s+1, f+1),
      from = 0, to = 1, ylab = "Posterior density")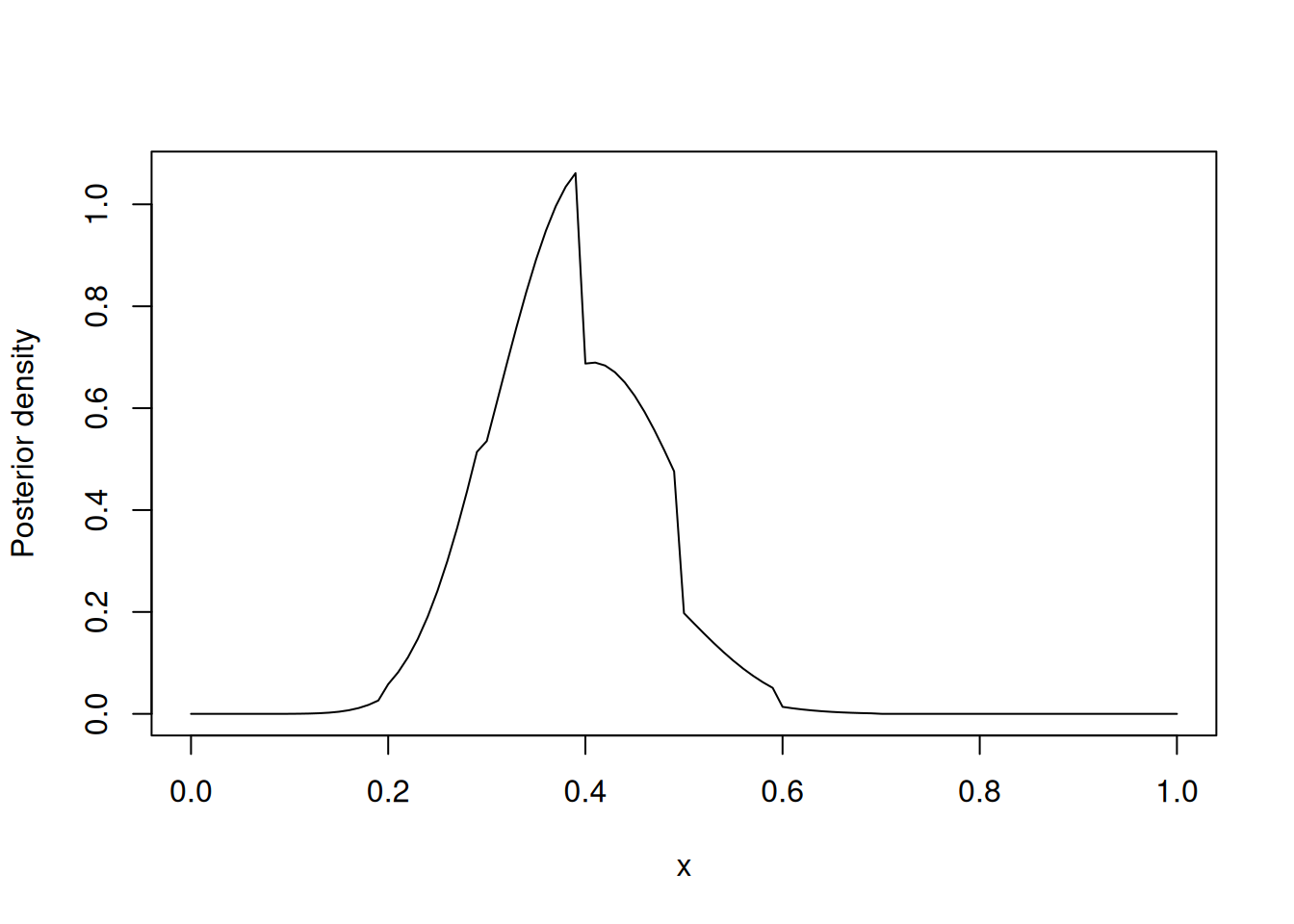

La posterior también se puede obtener de manera directa sin usar la función histprior:

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

PRIOR <- PRIOR %>% rename(prior = Probability)
datos_tot <- PRIOR %>% mutate(posterior = prior* p^(11)*(1-p)^(16)) %>%
  mutate(posterior = posterior/sum(posterior)) 
round(datos_tot$posterior,2)

 [1] 0.00 0.00 0.13 0.48 0.33 0.06 0.00 0.00 0.00 0.00

1.14.5 Simulación de la Distribución Posterior

Para obtener una muestra simulada de la posterior se procede de la siguiente manera:

1. Construir una rejilla de valores de \(p\) (por ejemplo, 500 puntos uniformemente distribuidos entre 0 y 1).
2. Calcular la densidad no normalizada en cada punto de la rejilla.
3. Normalizar los valores para obtener una distribución discreta.
4. Tomar una muestra con reemplazo utilizando la función sample.

# Crear una rejilla de valores para p
p = seq(0, 1, length = 500)

# Calcular la densidad no normalizada en cada punto de la rejilla
post = histprior(p, midpt, prior) * dbeta(p, s+1, f+1)
post = post / sum(post)  # Normalizar para obtener probabilidades

# Tomar una muestra simulada de la distribución posterior
ps = sample(p, replace = TRUE, prob = post)

Finalmente, se puede visualizar la muestra simulada mediante un histograma:

hist(ps, xlab = "p", main = "")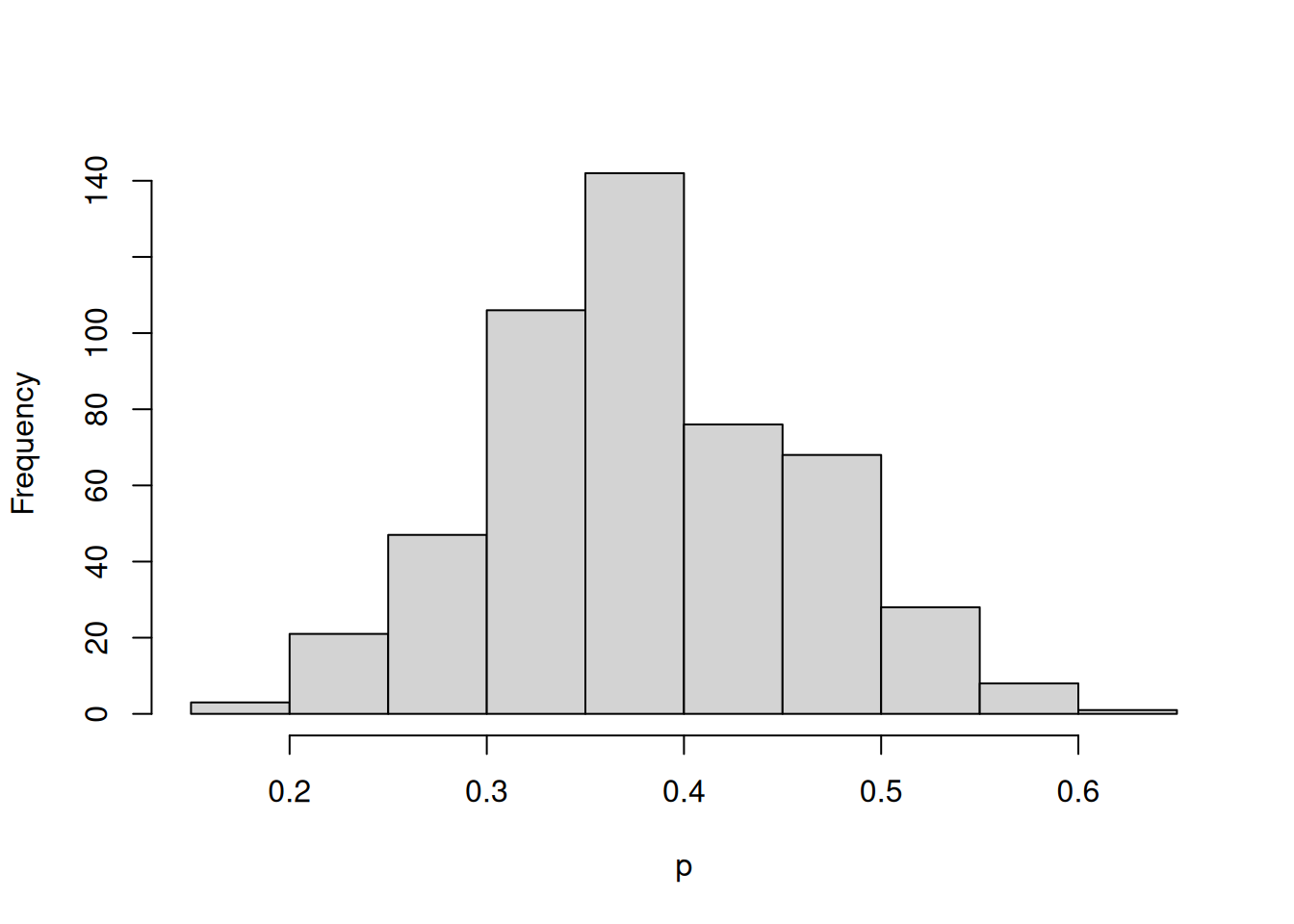

Los valores simulados se pueden utilizar para resumir cualquier característica de la distribución posterior de interés, por ejemplo, calcular intervalos de credibilidad o estimar probabilidades puntuales.

1.14.6 Predicción

En esta sección nos enfocamos en predecir el número de estudiantes que duermen lo suficiente (denotado por \(\tilde{y}\)) en una muestra futura de \(m=20\) estudiantes, basándonos en nuestras creencias actuales sobre la proporción \(p\). Si estas creencias se resumen en una densidad \(g(p)\), la densidad predictiva de \(\tilde{y}\) se define como:

\[ f(\tilde{y}) = \int f(\tilde{y} \mid p) \, g(p) \, dp. \]

Si \(g(p)\) es la densidad a priori, se le denomina densidad predictiva a priori; si es la densidad posterior, se le llama densidad predictiva posterior.

1.14.6.1 Predicción con una Prior Discreta

Supongamos que usamos una prior discreta, donde los posibles valores de \(p\), \(\{p_i\}\), tienen probabilidades asociadas \(\{g(p_i)\}\). Sea \(f_B(y \mid n, p)\) la densidad binomial para un tamaño muestral \(n\) y proporción \(p\):

\[ f_B(y \mid n, p) = \binom{n}{y} p^y (1-p)^{n-y}, \quad y=0,\ldots,n. \]

Entonces, la probabilidad predictiva de obtener \(\tilde{y}\) éxitos en una muestra futura de tamaño \(m\) es:

\[ f(\tilde{y}) = \sum_i f_B(\tilde{y} \mid m, p_i) \, g(p_i). \]

En R, utilizando el paquete LearnBayes, se puede calcular esta probabilidad con la función pdiscp. Por ejemplo:

p = seq(0.05, 0.95, by = 0.1)
prior = c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior = prior / sum(prior)
m = 20; ys = 0:20
pred = pdiscp(p, prior, m, ys)
round(cbind(0:20, pred), 3)

          pred
 [1,]  0 0.020
 [2,]  1 0.044
 [3,]  2 0.069
 [4,]  3 0.092
 [5,]  4 0.106
 [6,]  5 0.112
 [7,]  6 0.110
 [8,]  7 0.102
 [9,]  8 0.089
[10,]  9 0.074
[11,] 10 0.059
[12,] 11 0.044
[13,] 12 0.031
[14,] 13 0.021
[15,] 14 0.013
[16,] 15 0.007
[17,] 16 0.004
[18,] 17 0.002
[19,] 18 0.001
[20,] 19 0.000
[21,] 20 0.000

La salida muestra que los números de éxitos más probables en la muestra futura son \(\tilde{y}=5\) y \(\tilde{y}=6\).

1.14.6.2 Predicción con una Prior Beta

Si en lugar de una prior discreta modelamos nuestras creencias sobre \(p\) con una prior beta \((a,b)\), se puede obtener una expresión analítica para la densidad predictiva:

\[ f(\tilde{y}) = \binom{m}{\tilde{y}} \frac{B(a+\tilde{y},\, b+m-\tilde{y})}{B(a,b)}, \quad \tilde{y}=0,\ldots,m, \]

donde \(B(a,b)\) es la función beta. Las probabilidades predictivas se pueden calcular en R utilizando la función pbetap. Por ejemplo, para la prior beta \((3.26,7.19)\):

ab = c(3.26, 7.19)
m = 20; ys = 0:20
pred = pbetap(ab, m, ys)

1.14.6.3 Predicción por Simulación

Otra forma de obtener la densidad predictiva es mediante simulación. El procedimiento es el siguiente:

• Simular valores \(p^*\) de la densidad \(g(p)\).
• Para cada \(p^*\), simular \(\tilde{y}\) a partir de la distribución binomial \(f_B(\tilde{y} \mid m, p^*)\).

Por ejemplo, para una prior beta \((3.26, 7.19)\):

# Simular 1000 valores de p de la distribución beta
p = rbeta(1000, 3.26, 7.19)

# Simular 1000 valores de tilde{y} a partir de una binomial con tamaño m = 20
y = rbinom(1000, 20, p)

# Tabular y graficar la distribución predictiva
freq = table(y)
ys = as.integer(names(freq))
predprob = freq / sum(freq)
plot(ys, predprob, type = "h", xlab = "y", ylab = "Predictive Probability")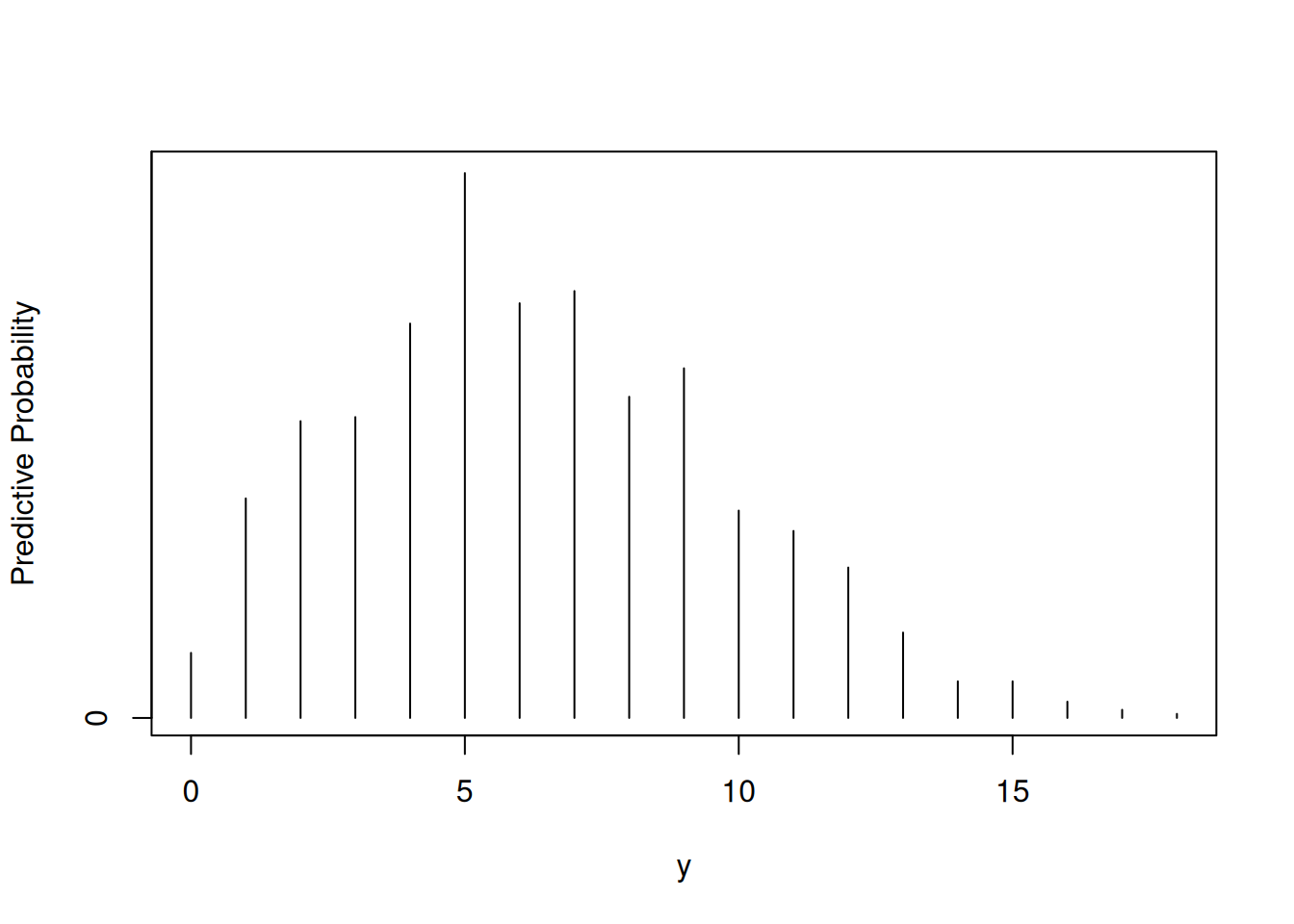

Además, para resumir esta distribución discreta predictiva mediante un intervalo que cubra al menos el \(90\%\) de la probabilidad, se puede usar la función discint del paquete LearnBayes. Por ejemplo:

dist = cbind(ys, predprob)
discint(dist, prob = 0.90)

$prob
    1 
0.908 

$set
 1  2  3  4  5  6  7  8  9 10 11 
 1  2  3  4  5  6  7  8  9 10 11 

La salida indicará, por ejemplo, que la probabilidad de que \(\tilde{y}\) se encuentre en el conjunto \(\{1,2,3,\ldots, 11\}\) es de aproximadamente \(91.8\%\). Esto equivale a decir que la proporción de “heavy sleepers” en la muestra futura, \(\tilde{y}/20\), estará en el intervalo \([1/20,\, 11/20]\) con una probabilidad del \(91.8\%\).