4 Computación Bayesiana

4.1 Cálculo de Integrales

En la práctica bayesiana, casi todas las inferencias se reducen a describir la distribución posterior de los parámetros. Dados unos datos $y$ con densidad de muestreo $f(y\mid\theta)$ y un prior $g(\theta)$, la ley de Bayes conduce a la posterior $g(\theta\mid y)\propto g(\theta)\,f(y\mid\theta).$ El reto no es escribirla, sino resumirla: necesitamos medias, varianzas, probabilidades o densidades marginales, y todas estas cantidades toman la forma de integrales sobre el espacio de $\theta$.

Por ejemplo, la media posterior de una función de interés $h(\theta)$ es

\[ \mathbb E\!\bigl[h(\theta)\mid y\bigr]= \frac{\int h(\theta)\,g(\theta)\,f(y\mid\theta)\,d\theta} {\int g(\theta)\,f(y\mid\theta)\,d\theta}. \]

Si lo que se desea es la probabilidad posterior de que $h(\theta)$ pertenezca a un conjunto $A$, basta restringir el dominio de integración al numerador:

\[ \mathbb P\!\bigl\{h(\theta)\in A\mid y\bigr\}= \frac{\int_{h(\theta)\in A} g(\theta)\,f(y\mid\theta)\,d\theta} {\int g(\theta)\,f(y\mid\theta)\,d\theta}. \]

Los mismos principios aparecen al marginalizar parámetros. Si $\theta=(\theta_1,\theta_2)$ y solo $\theta_1$ es relevante, se integra la parte “nuisance” $\theta_2$:

\[ g(\theta_1\mid y)\propto\int g(\theta_1,\theta_2\mid y)\,d\theta_2. \]

En teoría podría recurrirse a reglas de cuadratura clásicas para evaluar estas integrales. Sin embargo, su utilidad es limitada en problemas bayesianos reales. Primero, una cuadratura eficaz depende de conocer de antemano dónde está concentrada la masa posterior, algo que rara vez se sabe. Segundo, el costo computacional crece exponencialmente con la dimensión de $\theta$; incluso con técnicas adaptativas, la mal llamada “maldición de la dimensionalidad” hace impracticable la cuadratura cuando hay muchos parámetros.

Por estas razones, el resto del capítulo se centra en métodos numéricos específicamente diseñados para altas dimensiones—en particular, algoritmos de simulación (Monte Carlo, MCMC, etc.)—que permiten aproximar de forma general las integrales y, por ende, las inferencias bayesianas más complejas.

4.2 Definición del problema en R

Para que los algoritmos numéricos trabajen de manera correcta en algunos de los métodos que vamos a ver a continuación, lo primero es expresar la posterior de forma explícita (aunque sea sin la constante de normalización) y, acto seguido, reparametrizar todo parámetro restringido a valores reales. Un parámetro positivo se transforma al eje real con el logaritmo, mientras que una proporción $p$ se transforma mediante la función logit, $\operatorname{logit}(p)=\log\left(p/(1-p)\right)$. El objetivo es disponer finalmente de un vector $\theta=(\theta_1,\dots,\theta_k)\in\mathbb R^k$ apto para cualquier rutina de optimización o simulación.

La pieza clave es una función en R que devuelva el logaritmo de la densidad posterior. Su esqueleto básico es:

mylogposterior <- function(theta, data){
  ## Calcular aquí la log-densidad
  return(val)
}

theta es siempre un vector de dimensión $k$;
data contiene las observaciones y, si se necesita, hiperparámetros u otras constantes;
la salida es un escalar: el log-posterior evaluado en theta.

4.2.1 Ejemplo ilustrativo

Suponga un muestreo normal $y_i\sim\mathsf N(\mu,\sigma)$ con un prior $\mu\sim\mathsf N(10,20)$ y un previa uniforme sobre $\log\sigma$. Para evitar restricciones se trabaja con $\theta=(\mu,\log\sigma)$ y se codifica:

mylogposterior <- function(theta, data){

  mu    <- theta[1]
  sigma <- exp(theta[2])           # transforma de logσ a σ

  ## log-likelihood de cada y_i
  ll_i <- dnorm(data, mean = mu, sd = sigma, log = TRUE)

  ## log-prior sobre μ (gaussiano) + prior plano sobre logσ
  lp_mu <- dnorm(mu, mean = 10, sd = 20, log = TRUE)

  val <- lp_mu + sum(ll_i)         # log-posterior (constante ignorada)
  return(val)
}

El objeto mylogposterior() ya está listo para optimizadores (p. ej. optim) o para algoritmos futuros de muestreo posterior.

4.3 Modelo Beta–Binomial para Sobredispersión

Tsutakawa et al. (1985) estimaron las tasas de mortalidad por cáncer de estómago en varones de 45–64 años en las 20 ciudades más grandes de Missouri. Cada ciudad $j$ aporta el par $(y_j,n_j)$, donde $y_j$ es el número de muertes observado entre $n_j$ individuos en riesgo. Un modelo binomial simple, \[ y_j \sim \mathrm{Binomial}(n_j, p), \] supone una probabilidad común de muerte $p$, pero estos datos presentan sobredispersión, es decir, más variabilidad que la prevista por el modelo binomial.

Para captar la dispersión extra se usa el modelo beta–binomial, cuya función de masa es \[ f(y_j\mid \eta,K) =\binom{n_j}{y_j}\, \frac{B\bigl(K\eta + y_j,\;K(1-\eta)+n_j-y_j\bigr)} {B\bigl(K\eta,\;K(1-\eta)\bigr)}, \] donde $\eta$ es la tasa media de muertes y $K$ la precisión: a mayor $K$, más concentradas están las proporciones $y_j/n_j$ alrededor de $\eta$.

4.3.1 Priori y cálculo de la posterior

Se elige una priori vaga \[ g(\eta,K)\propto \frac{1}{\eta(1-\eta)}\,\frac{1}{(1+K)^2}, \quad 0<\eta<1,\;K>0. \] Combinando con la verosimilitud de las 20 ciudades, la posterior (sin normalizar) es \[ g(\eta,K\mid \text{datos}) \;\propto\; \frac{1}{\eta(1-\eta)}\,\frac{1}{(1+K)^2} \;\prod_{j=1}^{20} \frac{B\bigl(K\eta + y_j,\;K(1-\eta)+n_j-y_j\bigr)} {B\bigl(K\eta,\;K(1-\eta)\bigr)}. \]

4.3.2 Implementación en R

Definimos betabinexch0() para el logaritmo de la densidad posterior en $(\eta,K)$:

betabinexch0 = function(theta, data) {
  eta = theta[1]
  K   = theta[2]
  y   = data[,1]; n = data[,2]
  logf = function(y,n,K,eta)
    lbeta(K*eta + y, K*(1-eta) + n - y) -
    lbeta(K*eta, K*(1-eta))
  val = sum(logf(y, n, K, eta))
  val = val - log(eta) - log(1-eta) - 2*log(1+K)
  return(val)
}

Tras cargar los datos:

library(LearnBayes)


Attaching package: 'LearnBayes'

The following object is masked _by_ '.GlobalEnv':

    betabinexch0

data(cancermortality)
mycontour(betabinexch0,
          c(.0001,.003,1,20000),
          cancermortality,
          xlab="eta", ylab="K")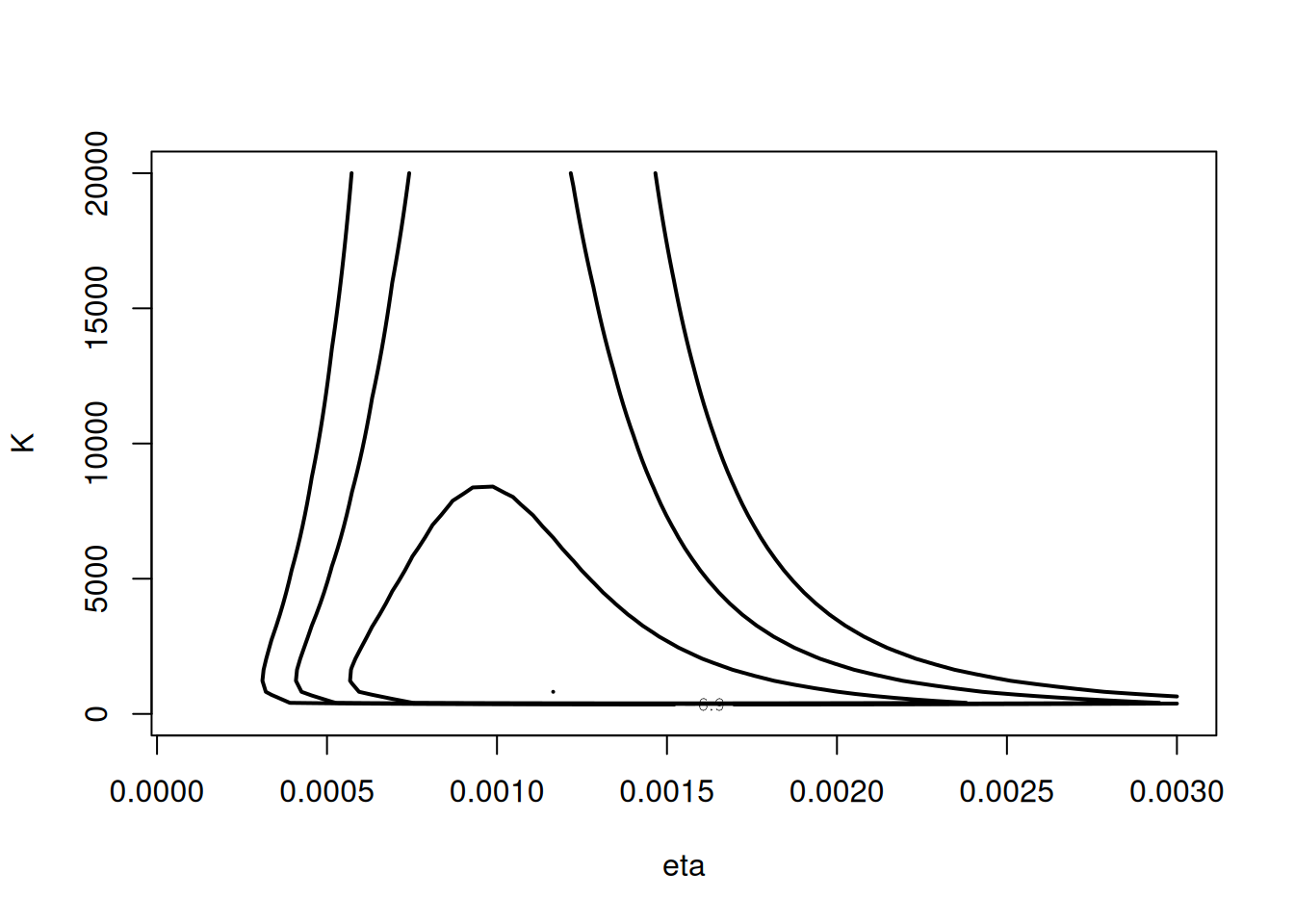

observamos un fuerte sesgo hacia valores grandes de $K$.

4.3.3 Reparametrización

Para trabajar en la recta real, definimos

\[ \theta_1 = \text{logit}(\eta) = \log\frac{\eta}{1-\eta},\quad \theta_2 = \log(K). \]

Incluyendo el Jacobiano, la función se modifica:

betabinexch = function(theta, data) {
  eta = exp(theta[1]) / (1 + exp(theta[1]))
  K   = exp(theta[2])
  y   = data[,1]; n = data[,2]
  logf = function(y,n,K,eta)
    lbeta(K*eta + y, K*(1-eta) + n - y) -
    lbeta(K*eta, K*(1-eta))
  val = sum(logf(y, n, K, eta))
  val = val + theta[2] - 2*log(1 + exp(theta[2]))
  return(val)
}

La posterior transformada se visualiza con:

mycontour(betabinexch,
          c(-8,-4.5,3,16.5),
          cancermortality,
          xlab="logit eta", ylab="log K")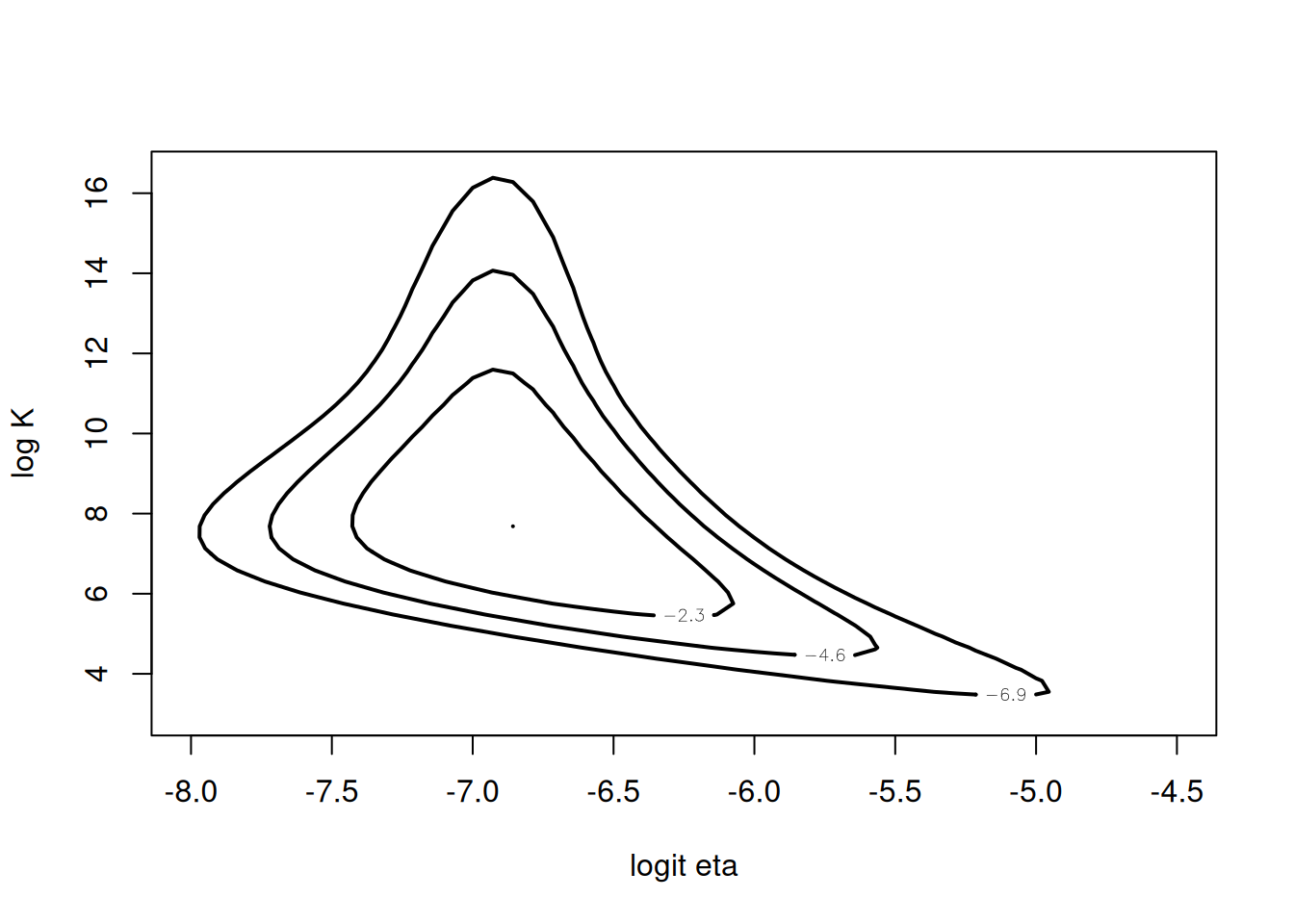

Esta transformación atenúa el sesgo y hace la superficie posterior más adecuada para métodos numéricos.

4.4 Aproximaciones basadas en modas posteriores (Laplace)

La técnica de Laplace aprovecha la forma local de la densidad posterior alrededor de su moda para construir una aproximación gaussiana. Sea $\theta\in\mathbb{R}^d$ el vector de parámetros, con priori $g(\theta)$ y verosimilitud $f(y\mid\theta)$. Definimos la función de interés,

\[ h(\theta)=\log\bigl(g(\theta)\,f(y\mid\theta)\bigr). \]

Denotando por $\hat\theta$ la moda posterior de $h(\theta)$, realizamos una expansión de Taylor de segundo orden en $\hat\theta$,

\[ h(\theta)\approx h(\hat\theta)+\tfrac12(\theta-\hat\theta)^\top\,h''(\hat\theta)\,(\theta-\hat\theta). \]

De aquí se deduce que la posterior se aproxima por una normal multivariada con media $\hat\theta$ y matriz de covarianza

\[ V=\bigl(-\,h''(\hat\theta)\bigr)^{-1}. \]

Esta aproximación también permite estimar la densidad predictiva previa de los datos:

\[ f(y)\approx(2\pi)^{d/2}\, g(\hat\theta)\,f(y\mid\hat\theta)\,\bigl|\,-h''(\hat\theta)\bigr|^{1/2}. \]

Para encontrar la moda posterior se recurre a algoritmos de optimización. El método de Newton itera

\[ \theta^{t}=\theta^{t-1} -\bigl[h''(\theta^{t-1})\bigr]^{-1}\,h'(\theta^{t-1}), \]

pero en la práctica es habitual usar el algoritmo Nelder–Mead (implementado en optim de R), más robusto ante malas elecciones del punto inicial. En el paquete LearnBayes, la función laplace encapsula estos pasos: requiere la función que evalúa $\log g(\theta\mid y)$, un valor inicial, y procede a devolver la moda, la matriz de varianza posterior estimada, la aproximación al logaritmo de la densidad predictiva y un indicador de convergencia.

4.4.1 Ejemplo

Para ilustrar la aproximación de Laplace usamos la función laplace sobre la versión transformada de los parámetros $(\text{logit}(\eta),\log K)$. Partimos de la estimación inicial $(-7,6)$ en el método de Nelder–Mead:

fit = laplace(betabinexch, c(-7,6), cancermortality)

El resultado reporta el modo posterior y su matriz de varianza asociada:

Moda (aproximación de $\bigl(\text{logit}(\eta),\log K\bigr)$):

  fit$mode

[1] -6.819793  7.576111

Matriz de varianza–covarianza $V$:

[,1] [,2]

[1] 0.07896568 –0.14850874

[2] –0.14850874 1.34832080

	[,1]	[,2]
[1]	0.07896568	–0.14850874
[2]	–0.14850874	1.34832080

fit$var

            [,1]       [,2]
[1,]  0.07896568 -0.1485087
[2,] -0.14850874  1.3483208

Log–predictivo aproximado: fit$int = -570.7743
Convergencia: fit$converge = TRUE

Bajo esta aproximación, $(\text{logit}(\eta),\log K)\approx\mathrm{N}(\hat\theta,,V)$. Podemos trazar sus contornos usando la densidad normal bivariante (lbinorm):

npar = list(m = fit$mode, v = fit$var)
mycontour(lbinorm, c(-8,-4.5,3,16.5), npar,
          xlab="logit eta", ylab="log K")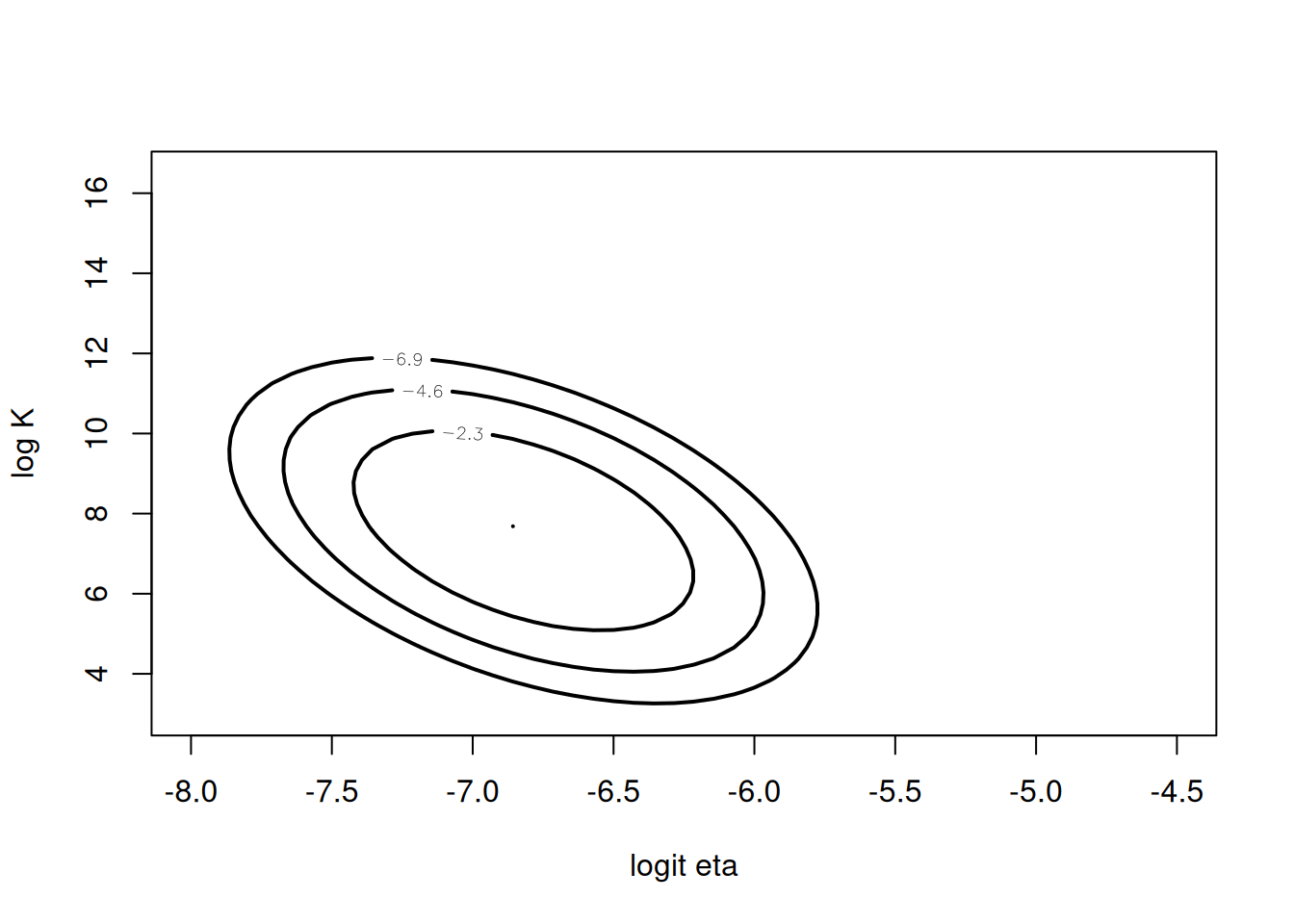

Finalmente, un intervalo de probabilidad aproximado al 90 % para cada componente se obtiene por la desviación estándar marginal:

se = sqrt(diag(fit$var))
fit$mode - 1.645 * se

[1] -7.282052  5.665982

fit$mode + 1.645 * se

[1] -6.357535  9.486239

Por tanto, un intervalo al 90 % para $\text{logit}(\eta)$ es $(-7.28,,-6.36)$ y para $\log K$ es $(5.67,,9.49)$.

Por lo tanto podemos sacar muestras posteriores de los parámetros transformados a través de una normal multivariada:

set.seed(10)
library(mvtnorm)
mu_sigma_post <- rmvnorm(1000,mean = npar$m,sigma = npar$v)

y graficamos los puntos sobre el gráfico de contorno:

mycontour(betabinexch,c(-8,-4.5,3,16.5),cancermortality,
            xlab="logit eta",ylab="log K")
points(mu_sigma_post,add=T)

Warning in plot.xy(xy.coords(x, y), type = type, ...): "add" is not a graphical
parameter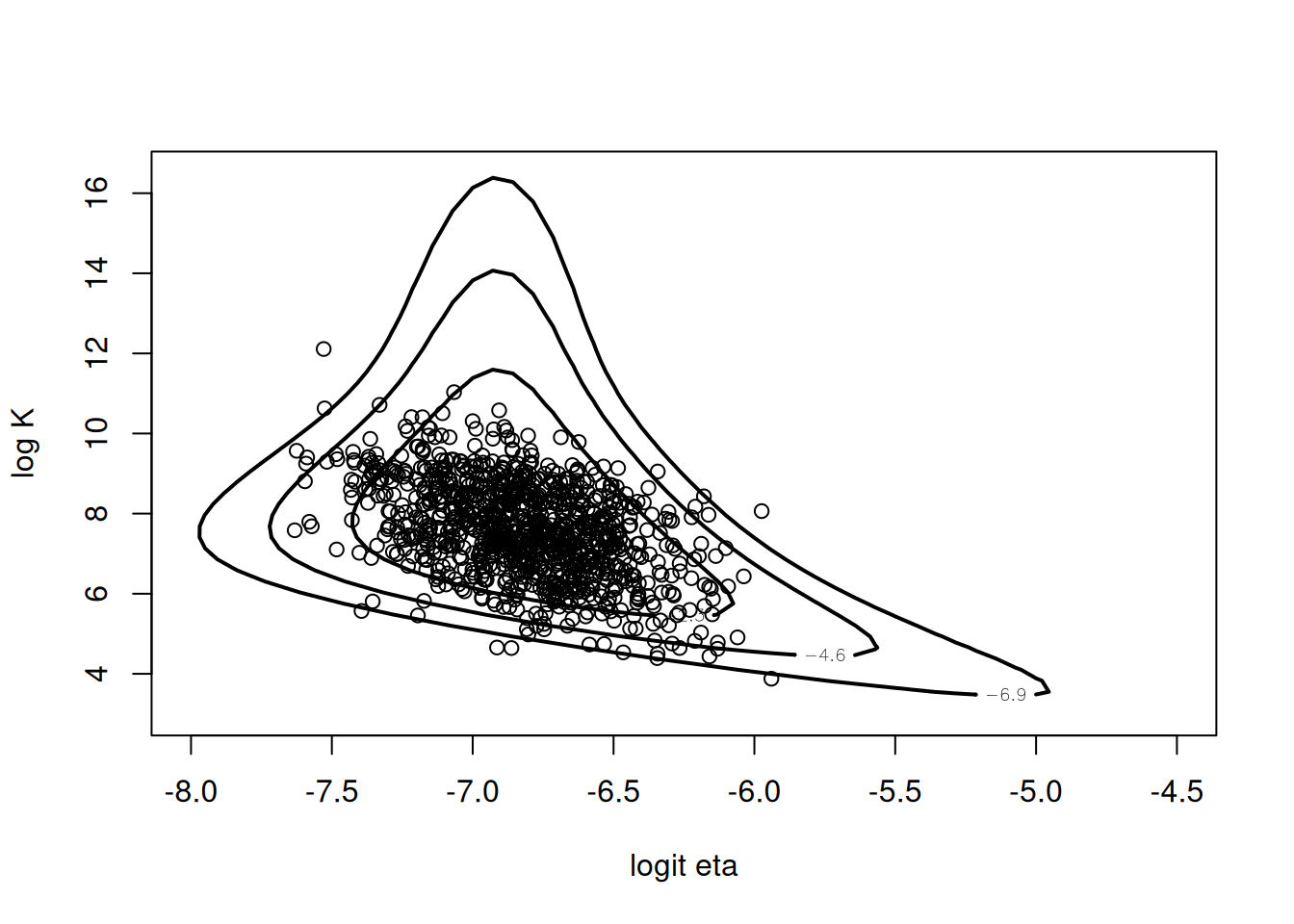

4.5 Método Monte Carlo para el cálculo de integrales

El enfoque Monte Carlo ofrece una forma sencilla y flexible de resumir distribuciones posteriores mediante simulación directa. Si disponemos de una muestra independiente

\[ \theta^{1},\dots,\theta^{m}\sim g(\theta\mid y), \]

podemos aproximar cualquier esperanza posterior de la forma

\[ E\bigl(h(\theta)\mid y\bigr)=\int h(\theta)\,g(\theta\mid y)\,d\theta \]

por el promedio de los valores simulados:

\[ \bar{h}=\frac{1}{m}\sum_{j=1}^m h\bigl(\theta^{j}\bigr). \]

La precisión de este estimador se cuantifica con el error estándar de simulación, calculado como

\[ se_{\bar{h}} =\sqrt{\frac{1}{m(m-1)}\sum_{j=1}^m\bigl[h(\theta^{j})-\bar h\bigr]^{2}}. \]

Para ilustrar esta idea, volvemos al ejemplo de la proporción de “heavy sleepers” universitarios. Con un prior Beta y datos que conducen a la posterior $\mathrm{Beta}(14.26,23.19)$, imaginemos que queremos estimar $\,E(p^{2}\mid y)$, es decir, la probabilidad de que dos estudiantes futuros sean ambos “dormilones”. Basta con simular de la posterior y calcular:

# Simulación Monte Carlo de p ~ Beta(14.26, 23.19)
set.seed(42)
p <- rbeta(1000, 14.26, 23.19)

# Estimador de E(p^2 | y) y su error estándar
est <- mean(p^2)
se  <- sd(p^2) / sqrt(1000)

# Resultado
c(Estimador = est, ErrorEstándar = se)

    Estimador ErrorEstándar 
  0.150157923   0.001881209

En este caso, obtendremos un estimador cercano a 0.15 con un error estándar alrededor de 0.002, lo que confirma la utilidad y simplicidad del método Monte Carlo para aproximar integrales posteriores cuando podemos simular de la distribución exacta.

4.6 Muestreo por rechazo

Cuando la posterior no corresponde a una forma conocida, no podemos simular directamente de ella y necesitamos un método general. El muestreo por rechazo parte de encontrar una densidad propuesta $p(\theta)$ fácil de muestrear que “cubra” a la posterior $g(\theta\mid y)$ en el sentido de que existe una constante $c$ tal que

\[ g(\theta\mid y)\le c\,p(\theta)\quad\text{para todo }\theta. \]

El algoritmo es sencillo:

Simular $\theta\sim p(\theta)$ y $U\sim\mathrm{Uniform}(0,1)$ independientes.
Aceptar $\theta$ si

\[ U \le \frac{g(\theta\mid y)}{c\,p(\theta)}, \]

en cuyo caso $\theta$ es una muestra válida de la posterior.
Rechazar en otro caso y repetir hasta obtener suficientes valores aceptados.

El reto está en elegir $p$ y $c$ para que la tasa de aceptación sea razonable.

4.6.1 Aplicación al ejemplo beta-binomial

En el modelo beta-binomial transformado $\theta=(\operatorname{logit}(\eta),\log K)$, usamos como propuesta una $t$ multivariada con media y escala basadas en la aproximación de Laplace (fit$mode, fit$var) y pocos grados de libertad (por ejemplo df = 4) para asegurar colas pesadas.

Primero, definimos una función que evalúa la diferencia logarítmica entre la posterior y la propuesta:

betabinT <- function(theta, datapar) {
  data <- datapar$data
  tpar <- datapar$par
  # log posterior original
  lg <- betabinexch(theta, data)
  # log densidad t multivariada
  lp <- dmt(theta, mean = tpar$m, S = tpar$var, df = tpar$df, log = TRUE)
  lg - lp
}

A continuación, configuramos los parámetros de la propuesta y buscamos el máximo de la diferencia con Laplace:

# t propuesta: media fit$mode, escala 2*fit$var, df = 4
tpar    <- list(m = fit$mode, var = 2 * fit$var, df = 4)
datapar <- list(data = cancermortality, par = tpar)

# optimizamos para hallar d = max [log g - log p]
start  <- c(-6.9, 12.4)
fit1   <- laplace(betabinT, start, datapar)
dmax   <- betabinT(fit1$mode, datapar)  # = log c

Por último, aplicamos el muestreo por rechazo con la función rejectsampling (disponible en LearnBayes), simulando 10 000 candidatos y quedándonos solo con los aceptados:

theta <- rejectsampling(
  logf   = betabinexch,  # log posterior original
  tpar   = tpar,         # parámetros de la t propuesta
  dmax   = dmax,         # cota logarítmica
  n      = 10000,        # candidatos
  data   = cancermortality
)
dim(theta)  # filas = número de aceptados

[1] 2459    2

En este caso la tasa de aceptación fue aproximadamente 0.24 (2459/10000). Al graficar los puntos sobre las curvas de nivel de la log–posterior, vemos que la mayoría cae en la zona de alta densidad, validando el método:

mycontour(betabinexch, c(-8,-4.5,3,16.5), cancermortality,
          xlab="logit eta", ylab="log K")
points(theta[,1], theta[,2], pch=20, cex=0.5)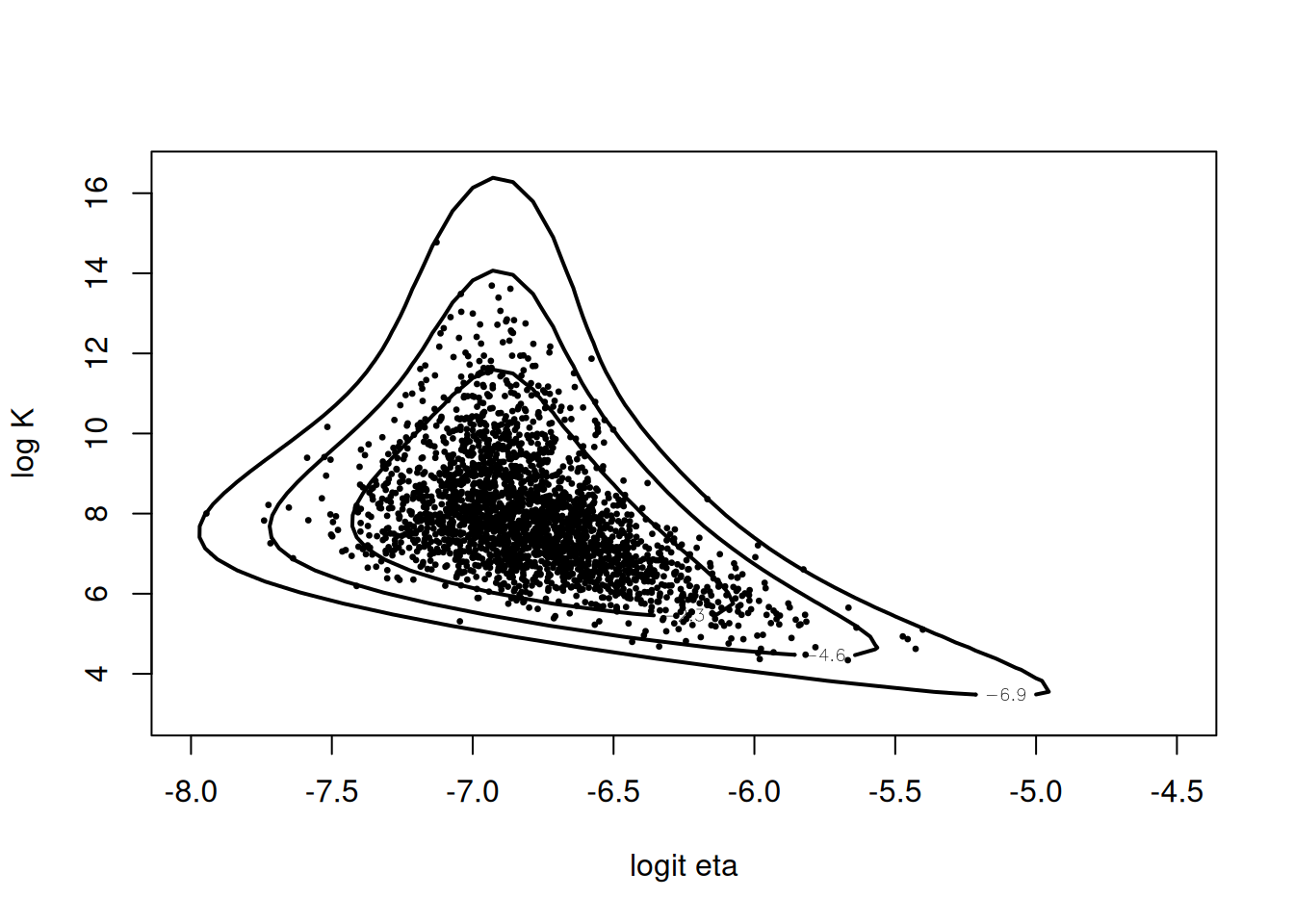

Aunque la aceptación es baja, el procedimiento es directo y útil cuando no hay formas cerradas para simular de la posterior.