library(GLMsData); data(lungcap)
lungcap$Smoke <- factor(lungcap$Smoke, levels = c(0, 1),labels = c("Non-smoker", "Smoker"))
LC.lm <- lm(FEV ~ Ht + Gender + Smoke, data = lungcap)2 Modelos de Regresión Lineal – Diagnósticos y Construcción de Modelos
Este capítulo enfatiza la importancia de los diagnósticos en modelos de regresión lineal. Una vez ajustado un modelo candidato, se emplean herramientas específicas para examinar y verificar los supuestos del modelo, detectar problemas y proponer soluciones que permitan construir un modelo robusto y adecuado para la inferencia y la predicción.
2.1 Introducción y Visión General
El proceso de construcción de un modelo de regresión se inicia con la exploración de los datos a través de gráficos, el diseño experimental y el conocimiento científico de las relaciones entre variables. Tras ajustar un modelo, se procede a realizar un análisis diagnóstico, que incluye:
- Verificación de supuestos: Revisión de la linealidad, homocedasticidad, independencia y normalidad.
- Análisis de residuos: Evaluar si los residuos cumplen con los supuestos del modelo.
- Detección de observaciones influyentes: Identificar puntos de alta influencia o valores atípicos.
- Evaluación de apalancamiento: Medir la posición de cada observación respecto al promedio de las variables explicativas.
2.2 Supuestos desde el Punto de Vista Práctico
El modelo de regresión lineal se expresa en su forma general o, asumiendo normalidad. Los supuestos fundamentales son:
- Ausencia de valores atípicos: Todos los \(y_i\) provienen del mismo proceso, lo que permite aplicar un único modelo a todas las observaciones.
- Linealidad: El predictor lineal describe correctamente la relación entre \(\mu_i\) y las variables explicativas, y se incluyen todas las variables importantes.
- Varianza constante: Las observaciones \(y_i\) tienen varianza constante (salvo por los pesos conocidos \(w_i\)).
- Independencia: Los \(y_i\) son estadísticamente independientes.
- Distribución normal: Los \(y_i\) se distribuyen normalmente en torno a \(\mu_i\).
La violación de estos supuestos puede afectar la precisión de las estimaciones, la validez de pruebas estadísticas y la interpretación de los parámetros.
2.3 Residuales para Modelos de Regresión Lineal Normales
En un modelo de regresión lineal, los residuales nos permiten evaluar la calidad del ajuste y diagnosticar posibles problemas en el modelo.
2.3.1 Residuales Crudos y su Variabilidad
Los residuales crudos se definen como:
\[ r_i = y_i - \hat{\mu}_i, \]
donde \(\hat{\mu}_i\) es el valor ajustado para la observación \(y_i\). La suma de cuadrados de los residuales se expresa como
\[ \mathrm{RSS} = \sum_{i=1}^{n} w_i \, r_i^2. \]
Dado que \(\hat{\mu}_i\) se estima a partir de los datos, es una variable aleatoria, por lo que
\[ \operatorname{var}[y_i - \hat{\mu}_i] \neq \operatorname{var}[y_i - \mu_i] = \operatorname{var}[y_i] = \frac{\sigma^2}{w_i}. \]
En realidad, se demuestra que:
\[ \operatorname{var}[r_i] = \frac{\sigma^2 (1-h_i)}{w_i} \tag{3.1} \]
donde \(h_i\) es el apalancamiento (leverage) de la observación \(y_i\), es decir, la medida de la influencia de \(y_i\) en el cálculo de su propio valor ajustado \(\hat{\mu}_i\). Esto indica que los residuales crudos no tienen varianza constante, lo cual puede dificultar su interpretación en gráficos diagnósticos.
2.3.2 Residuales Modificados y Estandarizados
Para obtener residuales con varianza constante, se define el residuo modificado:
\[ r_i^* = \frac{\sqrt{w_i} \, (y_i-\hat{\mu}_i)}{\sqrt{1-h_i}}, \]
de manera que
\[ \operatorname{var}[r_i^*] = \sigma^2. \]
Posteriormente, al estimar \(\sigma^2\) por \(s^2\), se definen los residuales estandarizados como:
\[ r_i' = \frac{r_i^*}{s} = \frac{\sqrt{w_i}\,(y_i-\hat{\mu}_i)}{s\,\sqrt{1-h_i}} \tag{3.2} \]
Estos residuales estandarizados representan la distancia estandarizada entre los valores observados \(y_i\) y los valores ajustados \(\hat{\mu}_i\). En general, \(r_i'\) se distribuye aproximadamente como una normal estándar, y de forma exacta sigue una distribución \(t\) con \(n-p'\) grados de libertad.
En R, se pueden obtener:
- Los residuales crudos con
resid(fit). - Los residuales estandarizados con
rstandard(fit).
2.3.3 Ejemplo: Datos de Capacidad Pulmonar
Para ilustrar estos conceptos, consideremos los datos de capacidad pulmonar (lungcap). En capítulos anteriores se usó la variable \(y = \log(\mathrm{FEV})\), pero aquí se modela \(y = \mathrm{FEV}\) para evidenciar cómo los diagnósticos revelan la inadecuación del modelo.
Se utiliza una componente sistemática con las variables Ht, Gender y Smoke (se prefiere Ht sobre Age ya que es una característica física):
Para calcular los residuales en R:
resid.raw <- resid(LC.lm) # Los residuales crudos
resid.std <- rstandard(LC.lm) # Los residuales estandarizados
c(Raw = var(resid.raw), Standardized = var(resid.std)) Raw Standardized
0.1812849 1.0027232 Como se observa, la varianza de los residuales estandarizados es aproximadamente uno, como se espera, lo que facilita su interpretación en los análisis diagnósticos.
2.4 Los Apalancamientos en Modelos de Regresión Lineal
Los apalancamientos (hat-values) son medidas que indican la influencia de cada observación en el ajuste de su propio valor predicho. Se derivan del “hat matrix” y dependen únicamente de los valores de las covariables (y de los pesos, si se usan).
2.4.1 Conceptos Básicos
Residuales Crudos Estandarizados:
Para estabilizar la varianza, se definen las respuestas estandarizadas: \[ z_i = \sqrt{w_i}\, y_i, \] de modo que \(E[z_i] = \sqrt{w_i}\,\mu_i\) y \(\operatorname{var}(z_i)=\sigma^2\).
Los valores ajustados estandarizados son \(\hat{\nu}_i = \sqrt{w_i}\,\hat{\mu}_i\), que se obtienen mediante una combinación lineal de los \(z_i\).Hat-Values y Apalancamientos:
Se definen los coeficientes \(h_{ij}\) que relacionan las respuestas estandarizadas \(z_j\) con los valores ajustados: \[ \hat{\nu}_i = \sum_{j=1}^n h_{ij}\,z_j. \] En particular, los elementos diagonales \(h_{ii}\) (denotados como \(h_i\)) miden el peso que la observación \(i\) tiene en el cálculo de su propio valor ajustado. Los \(h_i\) cumplen:- \(1/n \le h_i \le 1\), y su suma total es igual al número de parámetros estimados \(p'\).
- En promedio, \(\bar{h} = p'/n\).
Ejemplo en Regresión Simple:
Para un modelo de regresión simple sin pesos, \[ h_i = \frac{1}{n} + \frac{(x_i-\bar{x})^2}{\mathrm{SS}_x}, \] lo que muestra que el apalancamiento aumenta cuadráticamente a medida que \(x_i\) se aleja de la media \(\bar{x}\).
2.4.2 Interpretación de los Apalancamientos
- Un apalancamiento pequeño indica que la estimación de \(\hat{\mu}_i\) se basa en varias observaciones.
- Un apalancamiento alto (por ejemplo, dos o tres veces la media) indica una combinación inusual de covariables, pudiendo afectar en exceso el ajuste para esa observación.
- En el caso de variables categóricas, el apalancamiento para una observación dentro de un grupo es igual a \(1/n_j\), donde \(n_j\) es el número de observaciones en dicho grupo.
2.4.3 Matriz “Hat” y Cálculos en Álgebra Matricial
Para una regresión sin ponderación (\(w_i = 1\) para todos \(i\)), el estimador de mínimos cuadrados es: \[ \hat{\boldsymbol{\beta}} = (X^T X)^{-1} X^T y, \] y los valores ajustados son: \[ \hat{\boldsymbol{\mu}} = X \hat{\boldsymbol{\beta}} = H y, \] donde la matriz “hat” se define como: \[ H = X (X^T X)^{-1} X^T. \] Los elementos diagonales de \(H\), \(h_i = H_{ii}\), son los apalancamientos. Además, la varianza de los residuales se relaciona con los apalancamientos: \[ \operatorname{var}(r_i) = (1-h_i)\sigma^2. \]
Para el caso ponderado, se transforma el modelo usando \(\mathbf{z} = W^{1/2} y\) y \(X_w = W^{1/2}X\), obteniéndose: \[ H = W^{1/2} X (X^T W X)^{-1} X^T W^{1/2}. \tag{3.3} \]
2.4.4 Aplicación en R
En R, los apalancamientos se pueden obtener directamente con la función:
hatvalues(fit)donde es el objeto resultante de un modelo lineal (por ejemplo, creado con ).
2.4.4.1 Ejemplo
En el ejemplo de un “modelo pobre” para los datos de capacidad pulmonar (), se calcularon los apalancamientos:
h <- hatvalues(LC.lm) # LC.lm es el modelo ajustado
sort(h, decreasing = TRUE)[1:2] # Los dos apalancamientos más altos 629 631
0.02207842 0.02034224 Estos valores, comparados con la media de los apalancamientos (\(\bar{h} \approx 0.00612\)), indican que las observaciones 629 y 631 tienen una influencia mucho mayor en el ajuste, siendo identificadas como puntos inusuales (por ejemplo, ambos corresponden a hombres fumadores).
2.5 Gráficos de Residuales
Los gráficos de residuales son herramientas fundamentales para evaluar los supuestos del modelo de regresión lineal. Permiten detectar problemas de linealidad, heterocedasticidad (varianza no constante), no-normalidad y dependencia en el tiempo.
2.5.1 Gráfico de Residuales contra \(x_j\) (Linealidad)
- Propósito:
Verificar que, una vez eliminadas las contribuciones lineales de las demás variables, los residuales no muestran patrones sistemáticos en relación con cada covariable \(x_j\).
- Interpretación:
Si el modelo es adecuado, los residuales deben oscilar de forma aleatoria y mostrar varianza constante alrededor de cero. Cualquier tendencia (por ejemplo, curva cuadrática) sugiere que se requiere transformar la variable o incluir términos adicionales. - Herramienta en R:
Usarscatter.smooth()para agregar una curva suavizada y facilitar la detección de patrones.
Ejemplo en R:
# Graficar residuales estandarizados contra la variable 'Ht'
scatter.smooth(rstandard(LC.lm) ~ lungcap$Ht, col="grey",
las=1, ylab="Standardized residuals", xlab="Height (inches)")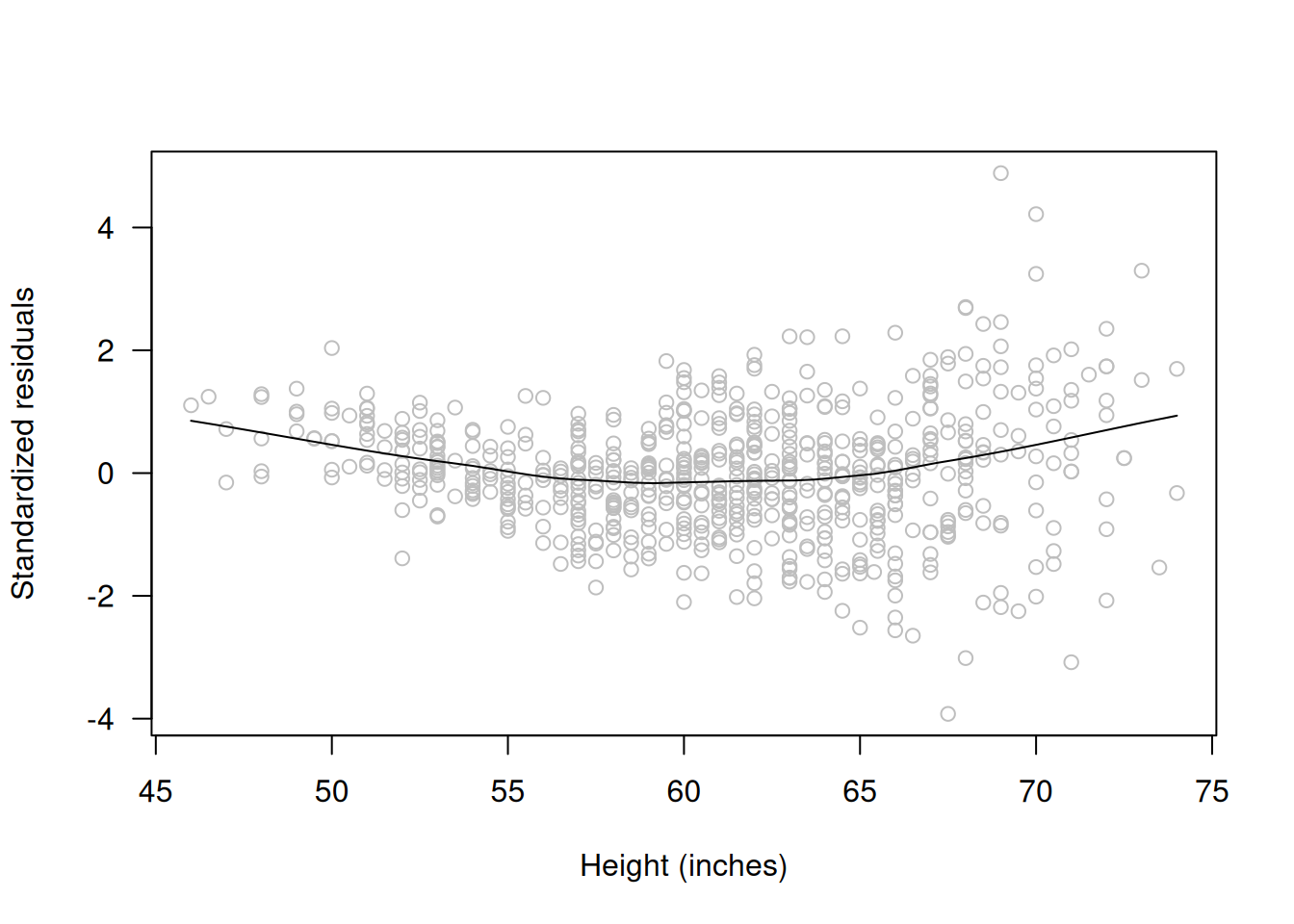
2.5.2 Gráficos de Residuales Parciales
- Definición:
Los residuales parciales se definen como: \[ u_j = r + \hat{\beta}_j \, x_j, \] donde \(r\) es el residual del modelo completo. - Propósito:
Permitir visualizar la contribución de una variable \(x_j\) tras ajustar por las demás. Facilita la evaluación de la linealidad y la importancia del efecto de \(x_j\) en el contexto del modelo múltiple. - Interpretación:
La pendiente de la línea de regresión en el gráfico de residuales parciales debe coincidir con \(\hat{\beta}_j\). Además, se puede evaluar si existe una tendencia no lineal respecto a \(x_j\).
# Calcular residuales parciales y graficarlos para la variable 'Ht'
partial.resid <- resid(LC.lm, type="partial")
termplot(LC.lm, partial.resid=TRUE, terms="Ht", las=1)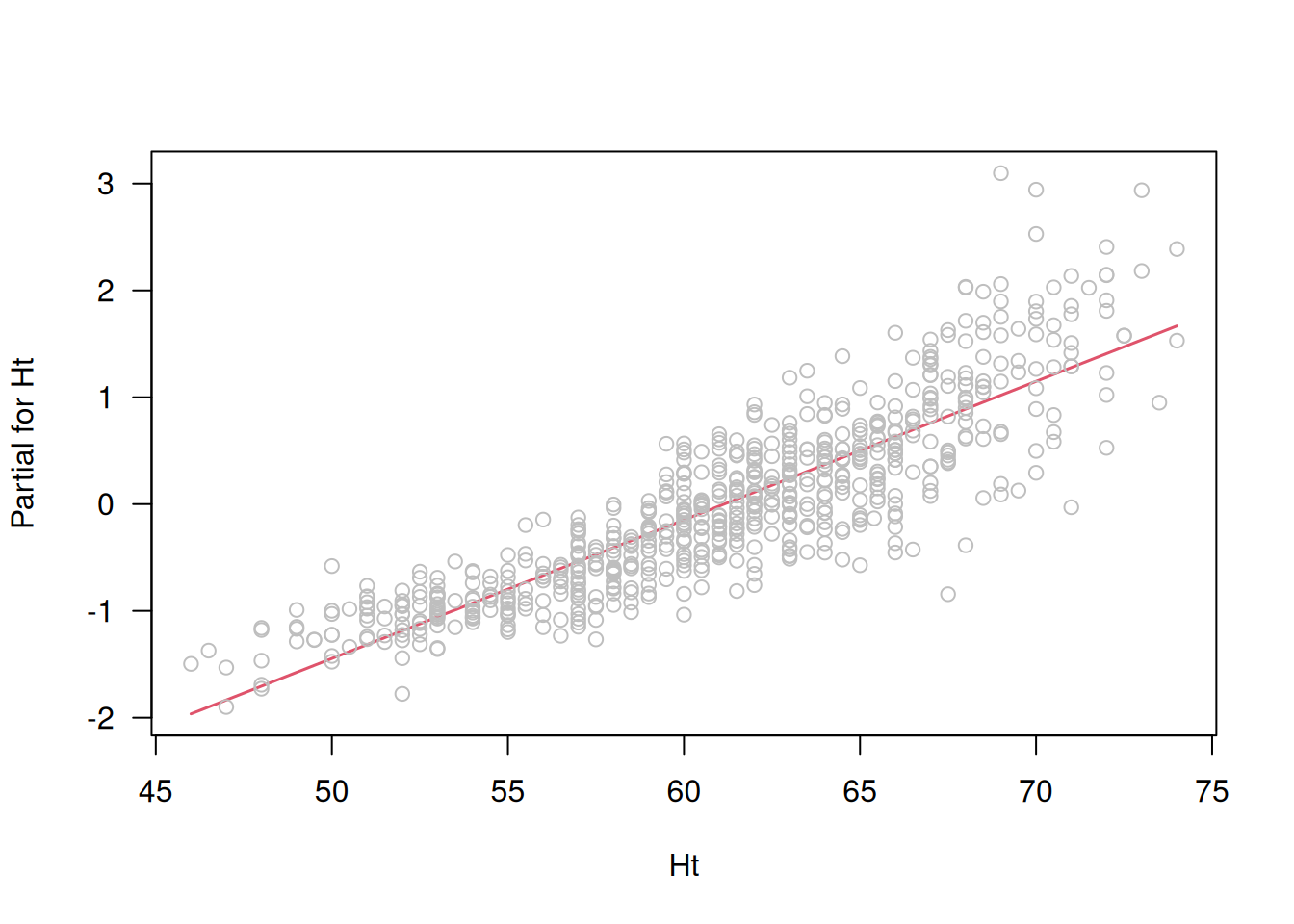
2.5.3 Gráficos de Residuales contra los Valores Ajustados \(\hat{\mu}\) (Varianza Constante)
- Propósito:
Evaluar la homocedasticidad (constancia de la varianza) de los residuales. - Interpretación:
Si la dispersión de los residuales aumenta o disminuye con los valores ajustados, es posible que exista un problema de heterocedasticidad. En esos casos, podría ser necesaria una transformación del \(y\) (por ejemplo, logaritmo). - Recomendación:
Es preferible utilizar residuales estandarizados, pues tienen varianza aproximadamente constante cuando el modelo se ajusta bien.
# Graficar residuales estandarizados contra los valores ajustados
scatter.smooth(rstandard(LC.lm) ~ fitted(LC.lm), col="grey",
las=1, ylab="Standardized residuals", xlab="Fitted values")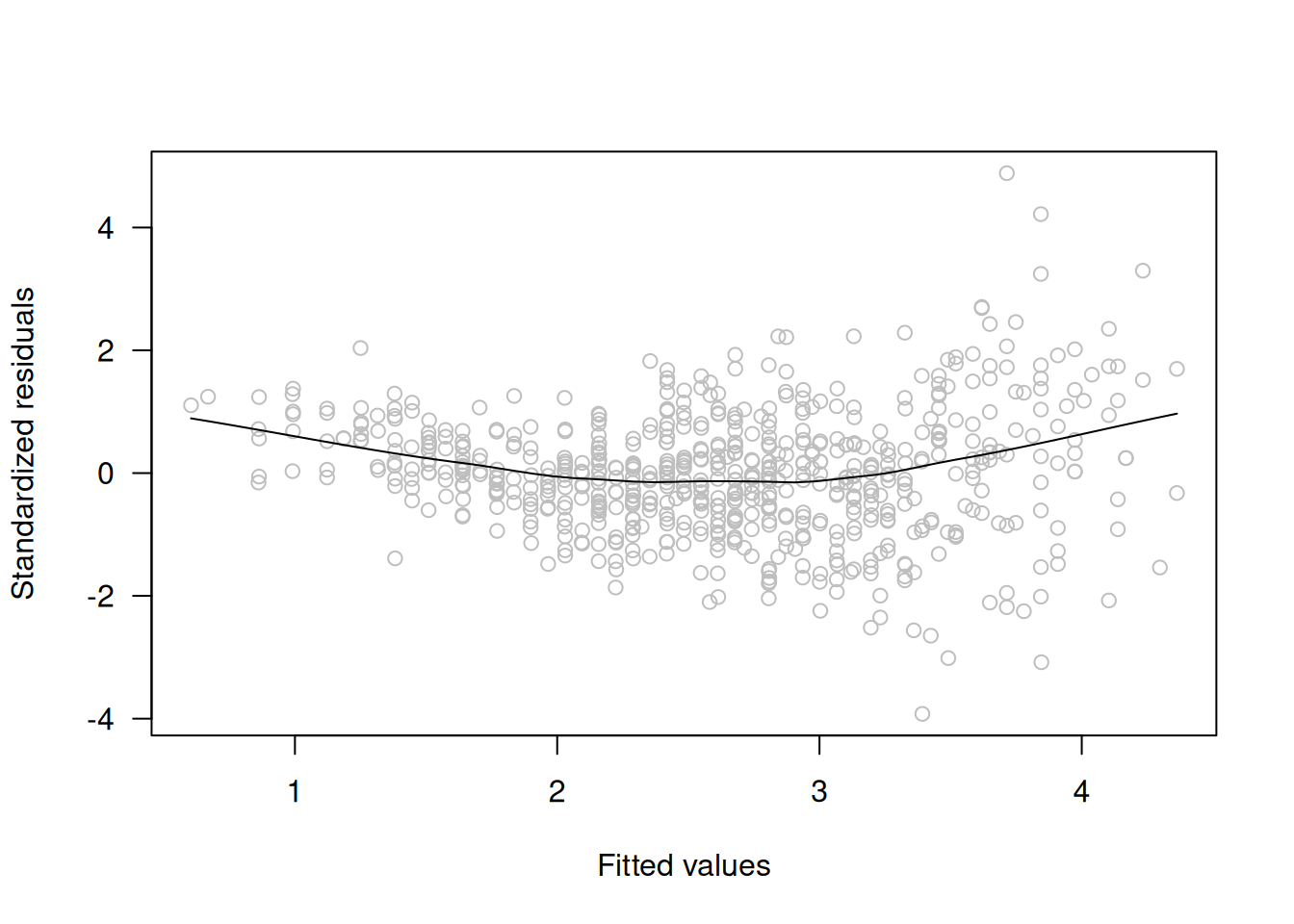
2.5.4 Q-Q Plots y Normalidad
- Propósito:
Verificar la suposición de normalidad de los residuales. - Interpretación:
Un gráfico Q-Q (quantile-quantile) confronta los cuantiles de los residuales (preferiblemente estandarizados) contra los cuantiles de una distribución normal estándar. Si los puntos siguen una línea recta, la normalidad es plausible. Desviaciones, como colas pesadas o asimetría, indican problemas de normalidad. - Herramienta en R:
Se utilizaqqnorm()para generar el gráfico yqqline()para agregar la línea de referencia.
# Crear el gráfico Q-Q de los residuales estandarizados
qqnorm(rstandard(LC.lm), las=1, pch=19)
qqline(rstandard(LC.lm)) # Agregar línea de referencia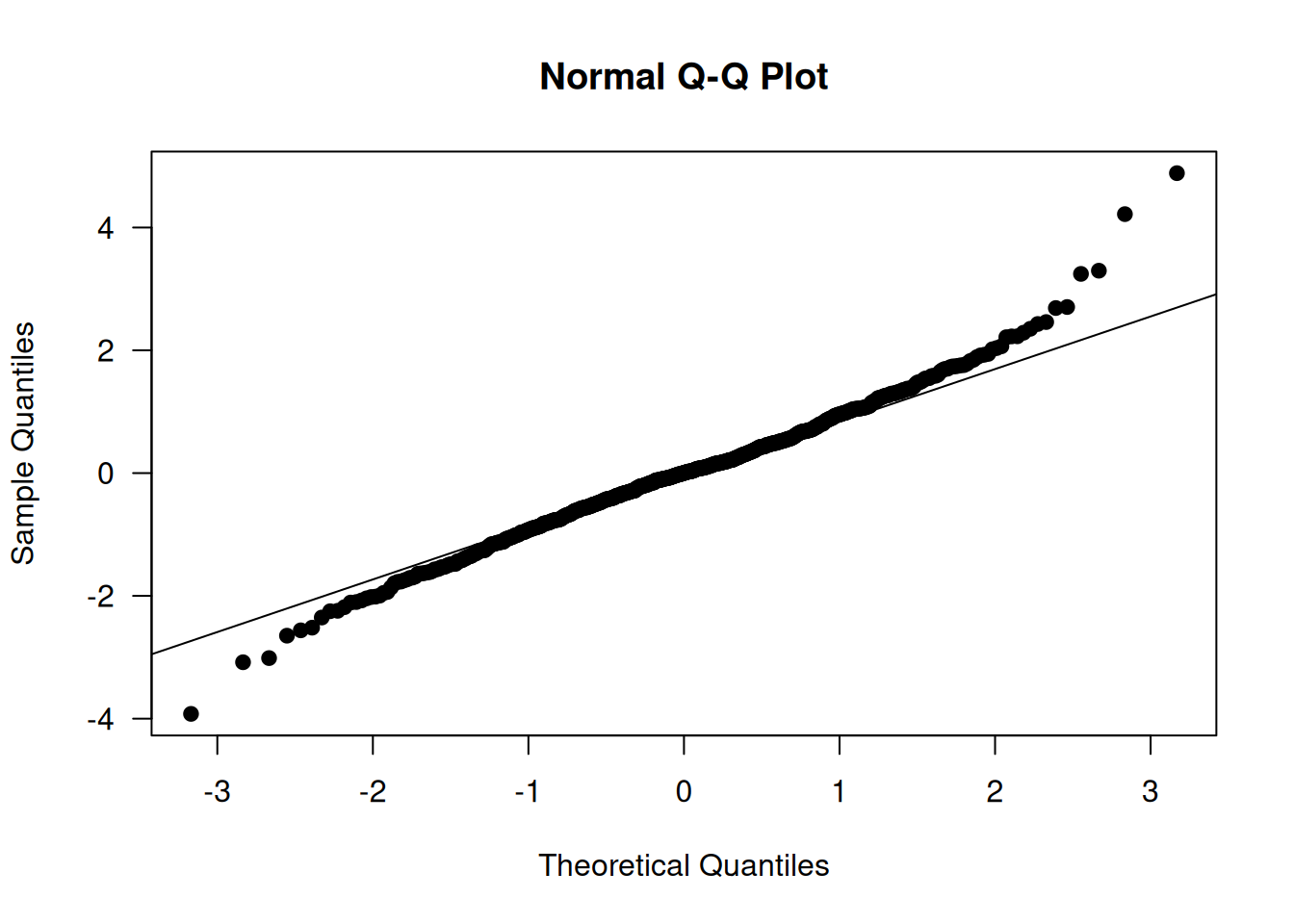
2.5.5 Lag Plots y Dependencia en el Tiempo
- Propósito:
Detectar la dependencia temporal entre residuales consecutivos, especialmente en datos de series de tiempo. - Interpretación:
Al graficar el residual en el tiempo \(r_t\) contra el residual anterior \(r_{t-1}\), la ausencia de patrones sugiere independencia. La presencia de patrones podría indicar autocorrelación y la necesidad de modelos que tengan en cuenta la dependencia temporal.
# Crear un lag plot de residuales estandarizados
r <- rstandard(LC.lm)
plot(r[-length(r)], r[-1], xlab="Residual at time t-1", ylab="Residual at time t",
main="Lag Plot", pch=19, col="blue")
2.6 Outliers y Observaciones Influyentes
En esta sección se presentan métodos para identificar problemas en el modelo de regresión a nivel de observación. Es decir, además de evaluar los supuestos globales del modelo, se analizan aquellos casos que pueden ser atípicos (outliers) o que influyen de manera excesiva en el ajuste del modelo.
2.6.1 Outliers y Residuales Studentizados
Outliers:
Son observaciones que son inconsistentes con el resto de los datos. Se pueden detectar cuando el residual estandarizado, \(r'\), es inusualmente grande (en valor absoluto), por ejemplo, mayor a 2.5.
Sin embargo, esto es solo una guía, ya que incluso en un modelo correctamente especificado, aproximadamente el 1.2% de las observaciones pueden superar este umbral por azar.Residuales Estandarizados vs. Studentizados:
Los residuales estandarizados se calculan usando el error estándar \(s^2\) estimado con todos los datos, lo que puede enmascarar la inusualidad de una observación.
Para mejorar la detección, se utilizan los residuales studentizados, que omiten la observación en cuestión al calcular \(s^2\). Se definen como: \[ r''_i = \frac{\sqrt{w_i} \, (y_i - \hat{\mu}_{i(i)})}{s_{(i)} \sqrt{1-h_i}}, \tag{3.5} \] donde \(\hat{\mu}_{i(i)}\) es el valor ajustado para la observación \(i\) cuando se omite del ajuste, y \(s_{(i)}^2\) es la varianza estimada sin la observación \(i\).
En R, los residuales studentizados se obtienen fácilmente con:rstudent(LC.lm)
Ejemplo
Para los datos de se observa que los residuales estandarizados y studentizados son muy similares:
summary(cbind(Standardized = rstandard(LC.lm),
Studentized = rstudent(LC.lm))) Standardized Studentized
Min. :-3.922299 Min. :-3.966502
1st Qu.:-0.596599 1st Qu.:-0.596304
Median : 0.002062 Median : 0.002061
Mean : 0.000213 Mean : 0.000387
3rd Qu.: 0.559121 3rd Qu.: 0.558826
Max. : 4.885392 Max. : 4.973802 2.7 Observaciones Influyentes
Las observaciones influyentes son aquellas que, al ser eliminadas, alteran significativamente el modelo ajustado. Una observación puede tener un residual grande pero no ser influyente si su valor en las covariables no es inusual (bajo apalancamiento). Por el contrario, un outlier con alto apalancamiento suele ser muy influyente.
2.7.1 Cook’s Distance
Una medida popular de influencia es la distancia de Cook, definida aproximadamente como: \[
D = \frac{(r')^2}{p'} \left(\frac{h}{1-h}\right), \tag{3.6}
\] donde \(r'\) es el residual estandarizado, \(h\) es el apalancamiento de la observación, y \(p'\) es el número total de parámetros en el modelo.
En R se calcula con:
cooks.distance(LC.lm)2.7.2 DFFITS y DFBETAS
DFFITS:
Mide el cambio en el valor ajustado de la observación \(i\) cuando ésta es omitida. Se define como: \[ \operatorname{DFFITS}_i = \frac{\hat{\mu}_i - \hat{\mu}_{i(i)}}{s_{(i)}} = r''_i \sqrt{\frac{h_i}{1-h_i}}. \] Se obtiene en R con:dffits(LC.lm)DFBETAS:
Son medidas específicas para cada coeficiente y cuantifican el cambio en cada \(\hat{\beta}_j\) cuando se omite la observación \(i\). Se definen como: \[ \operatorname{DFBETAS}_{ij} = \frac{\hat{\beta}_j - \hat{\beta}_{j(i)}}{\operatorname{se}(\hat{\beta}_{j(i)})}. \] En R se obtienen con:dfbetas(LC.lm)
2.7.3 Cociente de covarianza (CR)
El cociente de covarianza (CR) mide el aumento en la incertidumbre de los coeficientes cuando se omite una observación. Se calcula mediante: \[
\mathrm{CR} = \frac{1}{1-h} \left\{ \frac{n-p}{n-p' + (r'')^2} \right\}^{p},
\] donde \(r''\) es el residual studentizado.
En R, se usa:
covratio(LC.lm)2.7.4 Uso de la Función influence.measures()
La función en R genera una tabla con todas estas estadísticas (Cook’s D, DFFITS, DFBETAS, CR y los apalancamientos).
LC.im <- influence.measures(LC.lm)
names(LC.im)[1] "infmat" "is.inf" "call" La matriz contiene los valores de las medidas de influencia y indica si la observación es influyente según criterios predeterminados (por ejemplo, DFBETAS \(> 1\), DFFITS mayor que \(3/\sqrt{p'/(n-p')}\), CR alto, Cook’s D superior al percentil 50 del \(F\)-distribución y apalancamientos \(h > 3p'/n\)).
Ejemplo
Se identifican las observaciones con la mayor y menor distancia de Cook:
cd.max <- which.max(cooks.distance(LC.lm))
cd.min <- which.min(cooks.distance(LC.lm))
c(Min.Cook = cd.min, Max.Cook = cd.max) Min.Cook.69 Max.Cook.613
69 613 Luego se extraen los valores de DFFITS, Cook’s D y CR para estas observaciones:
out <- cbind(DFFITS = dffits(LC.lm),
Cooks.distance = cooks.distance(LC.lm),
Cov.ratio = covratio(LC.lm))
round(out[c(cd.min, cd.max), ], 5) DFFITS Cooks.distance Cov.ratio
69 0.00006 0.00000 1.01190
613 -0.39647 0.03881 0.96737Estos resultados indican que la observación 613 es más influyente que la 69, lo cual se confirma al examinar los cambios en los coeficientes utilizando .
Finalmente, para visualizar estas medidas, se pueden generar gráficos:
# Gráfico de Cook's Distance
plot(cooks.distance(LC.lm), type="h",
main="Cook's distance", ylab="D", xlab="Observation number", las=1)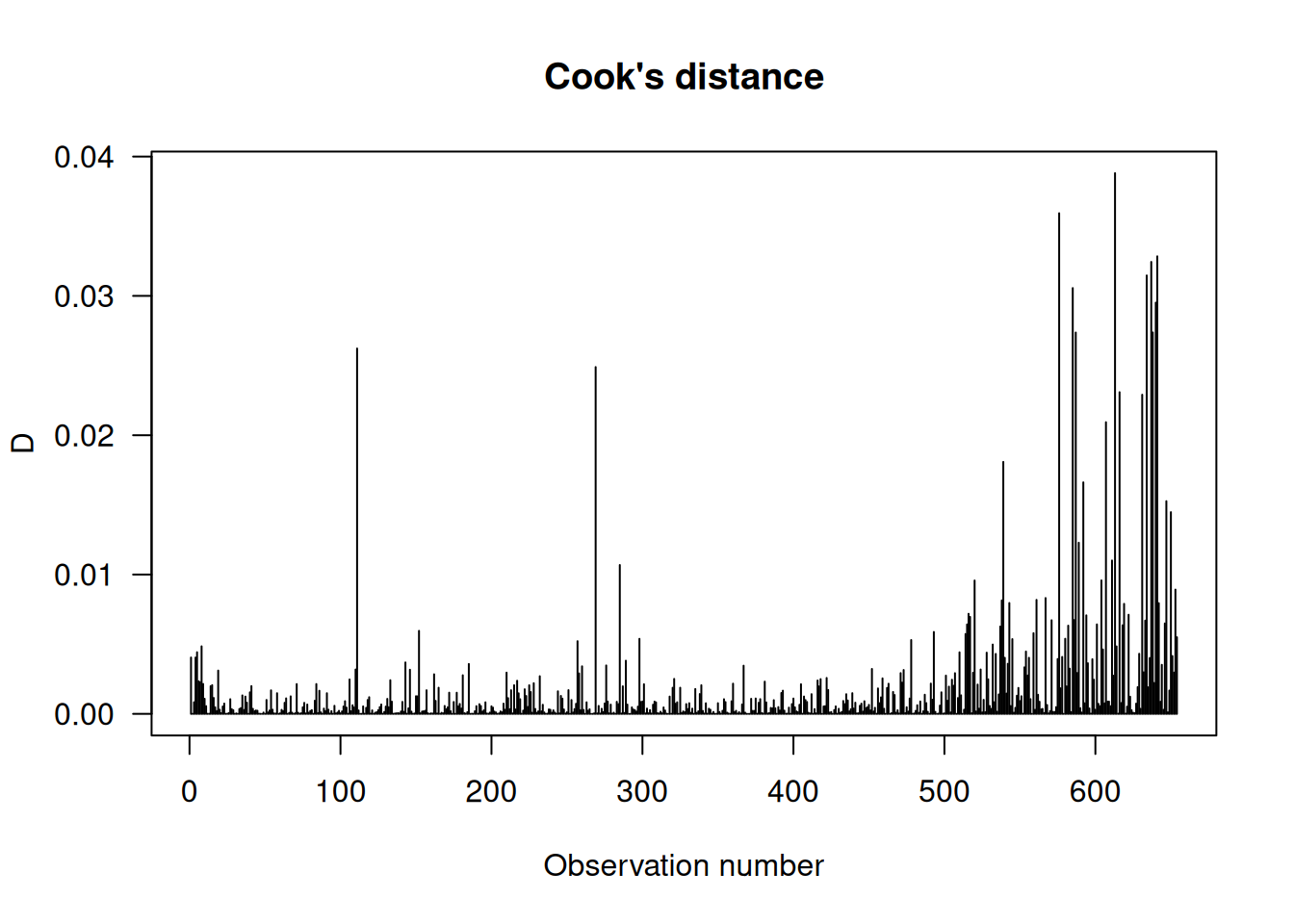
# Gráfico de DFFITS
plot(dffits(LC.lm), type="h",
main="DFFITS", ylab="DFFITS", xlab="Observation number", las=1)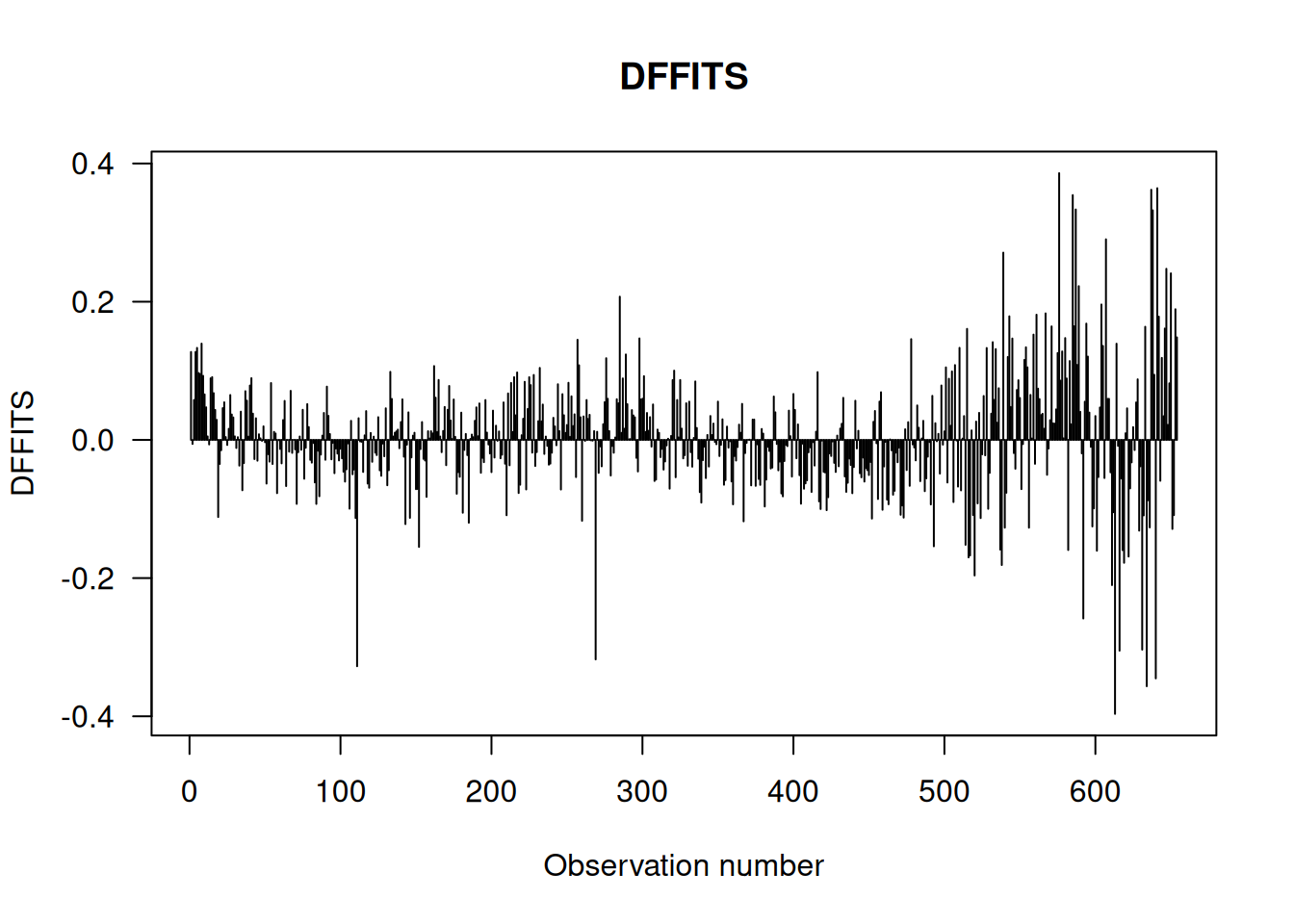
# Gráfico de DFBETAS para el coeficiente beta correspondiente a la variable 'Ht'
plot(dfbetas(LC.lm)[, 3], type="h",
main="DFBETAS para beta2", ylab="DFBETAS", xlab="Observation number", las=1)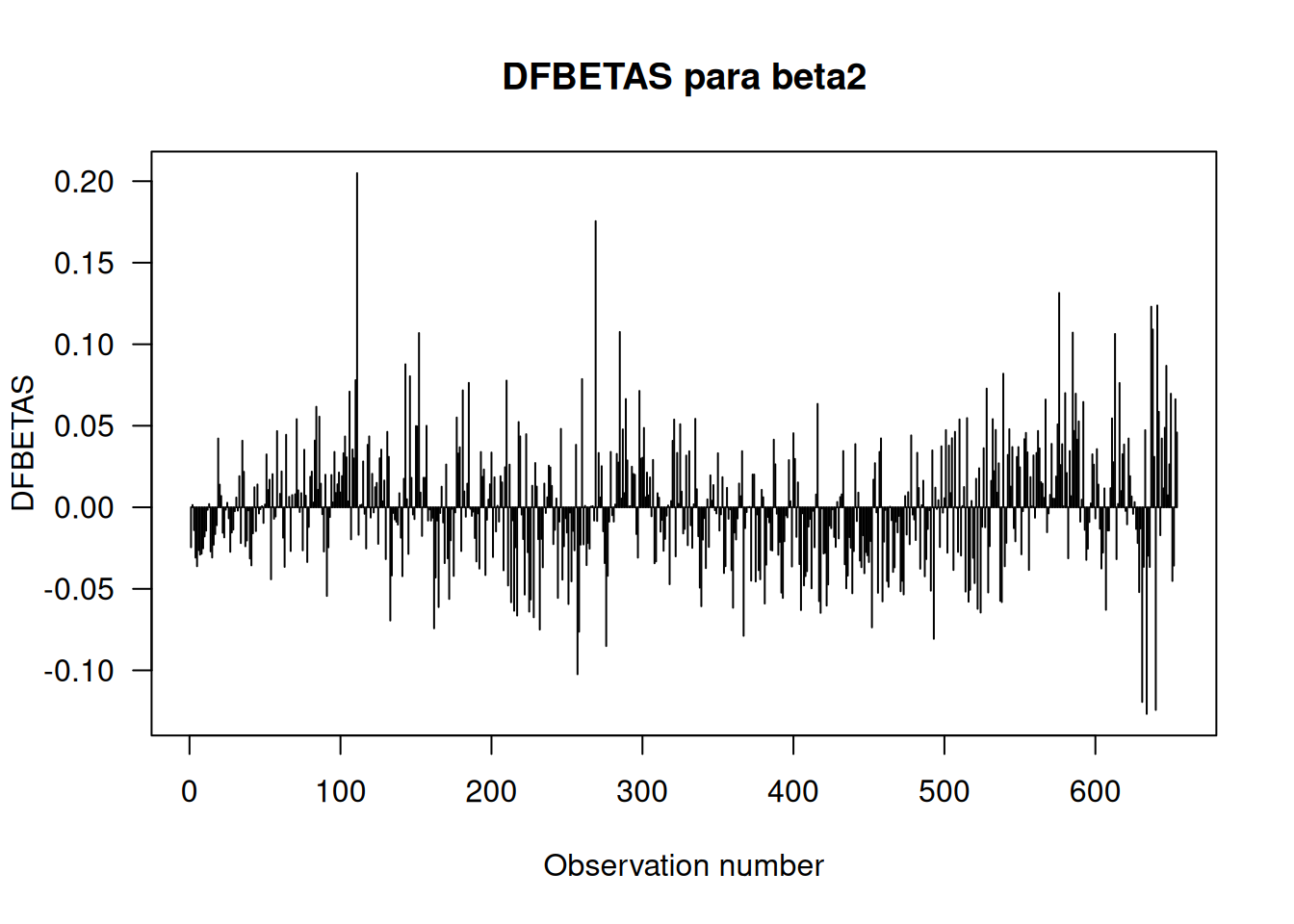
2.8 Solucionando Problemas Identificados
Una vez que se han utilizado los diagnósticos para detectar debilidades en el modelo de regresión, el siguiente paso es aplicar estrategias para corregir o mitigar esos problemas. A continuación se resumen las principales soluciones:
2.8.1 Transformación de la Variable Respuesta
Problema:
Cuando el \(y\) se mide en una escala en la que la varianza cambia (aumenta o disminuye) con la media, se observa una relación entre la media y la varianza (heterocedasticidad).Solución:
Transformar la variable respuesta puede estabilizar la varianza. Por ejemplo, si los valores de \(y\) son positivos y muestran mayor variabilidad a mayores niveles, se puede aplicar una transformación logarítmica u otra transformación apropiada.
2.8.2 Corrección de la No Linealidad
Problema:
Una relación no lineal entre \(y\) y una covariable \(x\) puede ser detectada en los gráficos de residuales o en los gráficos parciales de residuales.Solución:
Se puede:- Transformar la covariable \(x\) (por ejemplo, usando logaritmos, raíces o polinomios).
- Incluir términos adicionales en el modelo (por ejemplo, términos cuadráticos o cúbicos) para capturar la relación compleja.
Importante:
Generalmente, se recomienda fijar la escala de la variable respuesta \(y\) antes de transformar las covariables, ya que cualquier transformación de \(y\) afectará la forma de sus relaciones con las covariables.
2.8.3 Manejo de Outliers e Influencias
- Efecto:
Los cambios estructurales en el modelo (por transformación de \(y\) o inclusión de términos adicionales) suelen reducir la cantidad de outliers o observaciones altamente influyentes.
- Decisión:
Si aún persisten algunos outliers o casos de influencia excesiva, se debe decidir si:- Se eliminan esos puntos, o
- Se ajusta el modelo para acomodarlos (por ejemplo, mediante modelos robustos).
2.8.4 Problemas de Dependencia
- Problema:
Las correlaciones entre los residuales pueden surgir por causas comunes o por estructuras de muestreo (por ejemplo, medidas repetidas, bloques, series temporales). - Solución (más avanzado):
Aunque este tema se menciona como un posible problema, existen modelos más complejos para tratar la dependencia, tales como:- Modelos de mínimos cuadrados generalizados (GLS),
- Modelos mixtos (mixed models),
- Modelos espaciales.
2.9 Transformación de la Respuesta
Transformar la variable respuesta consiste en convertir \(y\) a una nueva escala, \(y^*=h(y)\), en la cual se espera que se cumplan mejor los supuestos del modelo (linealidad, normalidad y varianza constante). Esta estrategia es especialmente útil cuando la escala original de \(y\) está limitada (por ejemplo, solo valores positivos) o cuando presenta asimetría y una relación media-varianza (heterocedasticidad).
2.9.1 Simetría, Restricciones y la Escalera de Potencias
Idea:
Una transformación, por ejemplo, el logaritmo, puede cambiar la escala de medición.
\[ \text{Ejemplo: } \quad \mathrm{pH} = -\log_{10} y, \] donde \(y\) es la concentración de iones de hidrógeno. Esto permite trabajar en una escala donde la variable no tiene restricciones (la línea de regresión es no acotada) y donde los coeficientes pueden interpretarse de forma más adecuada.La Escalera de Potencias:
Se utiliza una “escalera de potencias” para transformar \(y\), que consiste en aplicar potencias de \(y\) con exponentes (\(\lambda\)) que varían.- Para \(y\) con asimetría positiva y/o una varianza que aumenta con la media, se recomiendan transformaciones con \(\lambda < 1\), como por ejemplo el logaritmo (\(\lambda=0\)) o potencias menores (por ejemplo, \(y^{1/2}\)).
- Si \(y\) es asimétrica en dirección contraria, se pueden usar transformaciones con \(\lambda > 1\).
La elección de \(\lambda\) se realiza de forma iterativa, buscando que los residuales muestren simetría y varianza constante.
- Para \(y\) con asimetría positiva y/o una varianza que aumenta con la media, se recomiendan transformaciones con \(\lambda < 1\), como por ejemplo el logaritmo (\(\lambda=0\)) o potencias menores (por ejemplo, \(y^{1/2}\)).
2.9.2 Transformaciones para Estabilizar la Varianza
Motivación:
A menudo, cuando \(y\) es una cantidad física positiva, la varianza aumenta con la media. Esto se conoce como una relación media-varianza positiva.
Por ejemplo, si la varianza de \(y\) es proporcional a \(\mu^2\), es decir, \[ \operatorname{var}(y)=\phi \mu^2, \] entonces la transformación logarítmica es apropiada por el método delta, ya que \[ \frac{d}{d\mu} (\log \mu)=\frac{1}{\mu}. \]Generalización:
En términos generales, si \(y\) tiene una relación media-varianza descrita por \(V(\mu)\), se busca una transformación \(y^*=h(y)\) tal que \[ h'(\mu) \propto V(\mu)^{-1/2}. \]- Si \(V(\mu)=\mu^2\), se usa \(h(y)=\log y\).
- Si \(V(\mu)=\mu\), se utiliza la transformación raíz cuadrada.
- Si \(V(\mu)=\mu^2\), se usa \(h(y)=\log y\).
2.9.3 Transformaciones de Box-Cox
Las transformaciones de Box-Cox son una familia de transformaciones de potencia definidas por: \[ y^* = \begin{cases} \displaystyle \frac{y^{\lambda} - 1}{\lambda}, & \lambda \neq 0, \\[2ex] \log y, & \lambda = 0. \end{cases} \tag{3.8} \] Esta forma es continua en \(\lambda\) y permite elegir, de manera sistemática, la transformación que optimice simultáneamente la linealidad, la normalidad y la homocedasticidad de los residuales.
2.9.4 Ejemplo
Se ha observado que el modelo ajustado a los datos de capacidad pulmonar (FEV) presenta problemas de heterocedasticidad y no linealidad. Para evaluar transformaciones en la variable respuesta se puede proceder de la siguiente manera:
2.9.4.1 Transformación con Raíz Cuadrada
LC.sqrt <- update(LC.lm, sqrt(FEV) ~ .)
scatter.smooth(rstandard(LC.sqrt) ~ fitted(LC.sqrt), las=1, col="grey",
ylab="Standardized residuals", xlab="Fitted values",
main="Square-root transformation")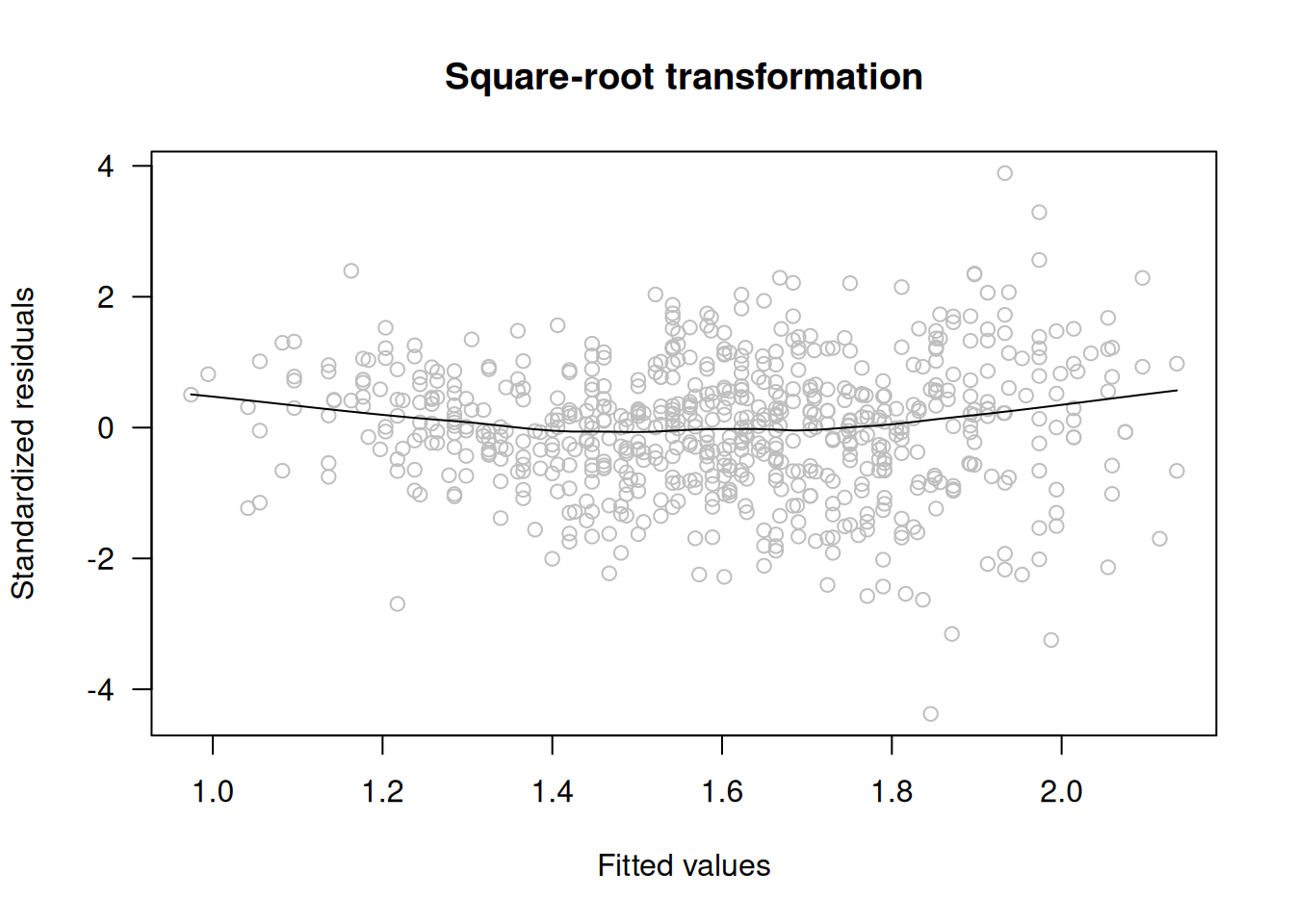
Esta transformación produce una varianza ligeramente creciente.
2.9.4.2 Transformación Logarítmica
LC.log <- update(LC.lm, log(FEV) ~ .)
scatter.smooth(rstandard(LC.log) ~ fitted(LC.log), las=1, col="grey",
ylab="Standardized residuals", xlab="Fitted values",
main="Log transformation")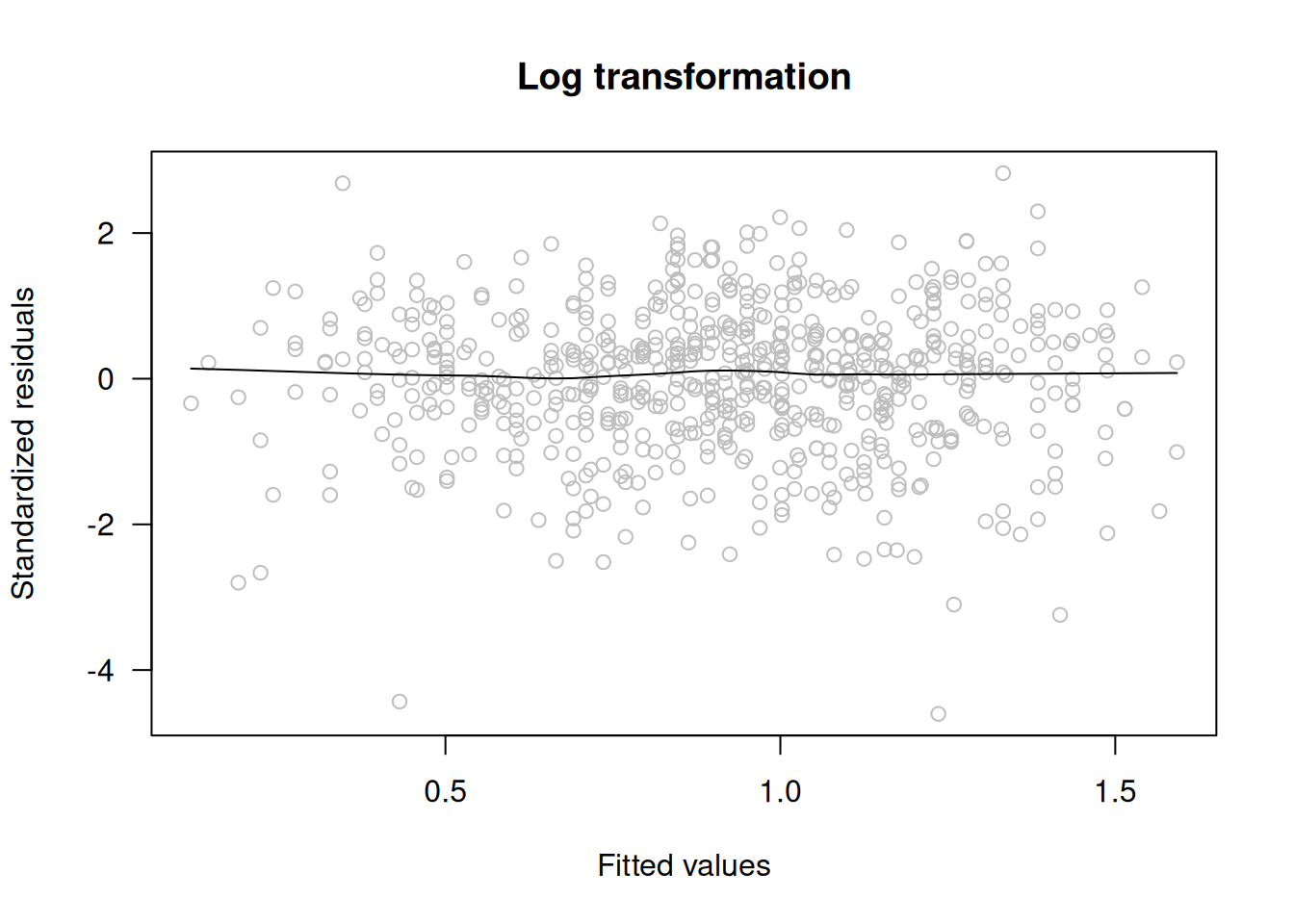
El gráfico resultante muestra varianza constante y ausencia de tendencia, lo que sugiere que la transformación logarítmica es adecuada para estabilizar la varianza y mejorar la linealidad del modelo.
2.9.4.3 Uso de la Transformación Box-Cox
Para determinar el valor óptimo de \(\lambda\), se utiliza la función boxcox() del paquete MASS:
library(MASS)
boxcox(FEV ~ Ht + Gender + Smoke, lambda=seq(-0.25, 0.25, length=11), data=lungcap)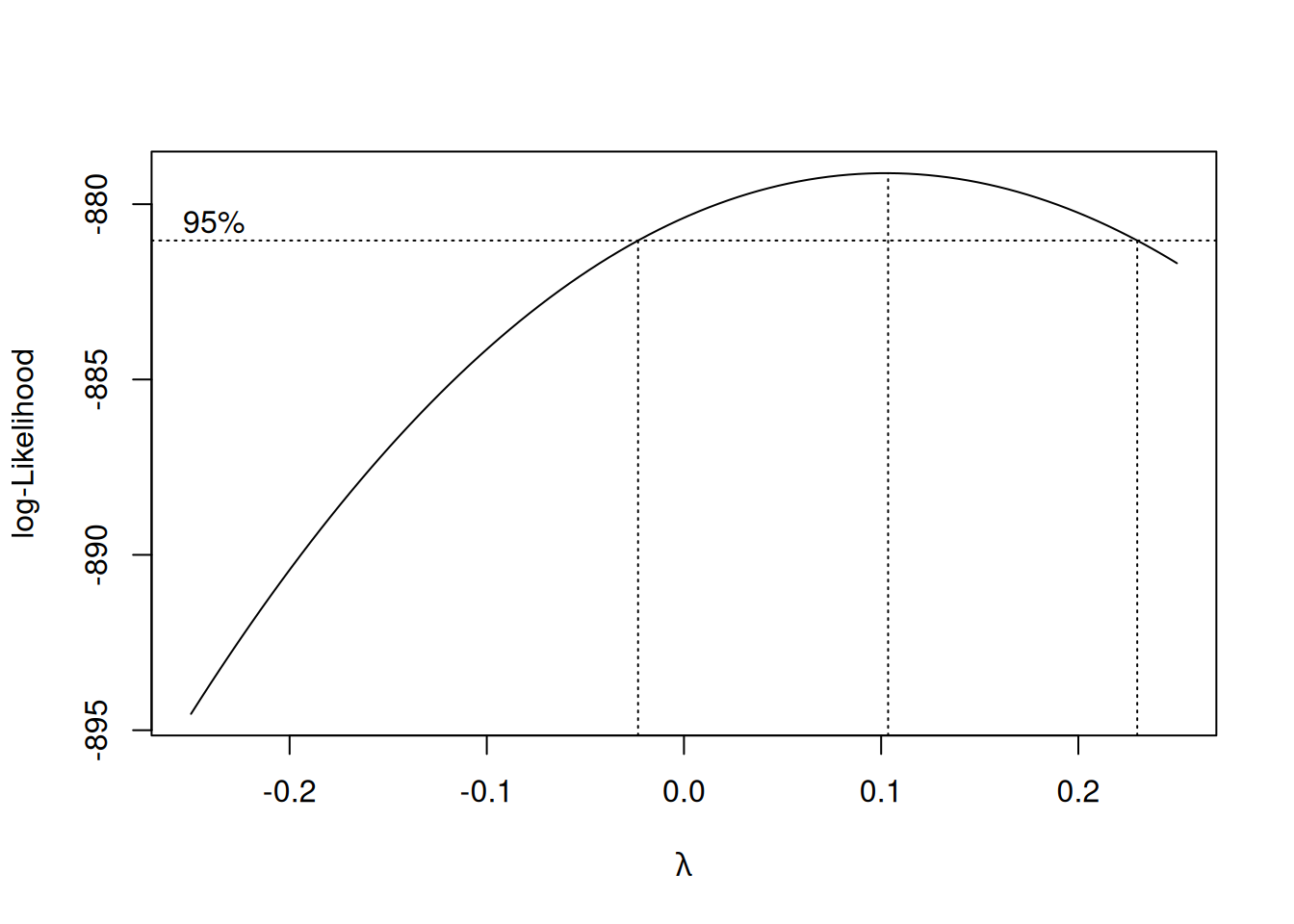
El gráfico generado indica que el logaritmo (es decir, \(\lambda \approx 0\)) es casi óptimo para lograr linealidad, normalidad y varianza constante en el modelo.
2.10 Transformaciones Simples de Covariables
A veces, para lograr una relación lineal o para reducir la influencia de observaciones influyentes, es necesario transformar las covariables. Al transformar las covariables se mantiene la linealidad en los parámetros, ya que el modelo sigue siendo lineal en ellos. Es importante notar que transformar variables categóricas (factores) no tiene sentido.
2.10.1 Objetivos de Transformar Covariables
Lograr linealidad:
Al eliminar la curvatura o patrones no lineales en la relación entre la respuesta y la covariable, se facilita el ajuste del modelo.Reducir la influencia de observaciones influyentes:
Transformaciones pueden disminuir el efecto de valores extremos en las covariables, lo que a su vez reduce su influencia excesiva en el ajuste del modelo.
2.10.2 Ejemplo con Datos de Aerogeneradores
Se registraron la velocidad del viento y la salida de corriente continua (DC) de aerogeneradores (data set: windmill).
Un primer gráfico de dispersión del DC frente a la velocidad del viento muestra una relación no lineal, aunque la varianza parece constante:
data(windmill); names(windmill)[1] "Wind" "DC" scatter.smooth(windmill$DC ~ windmill$Wind, main="No transforms",
xlab="Wind speed", ylab="DC output", las=1)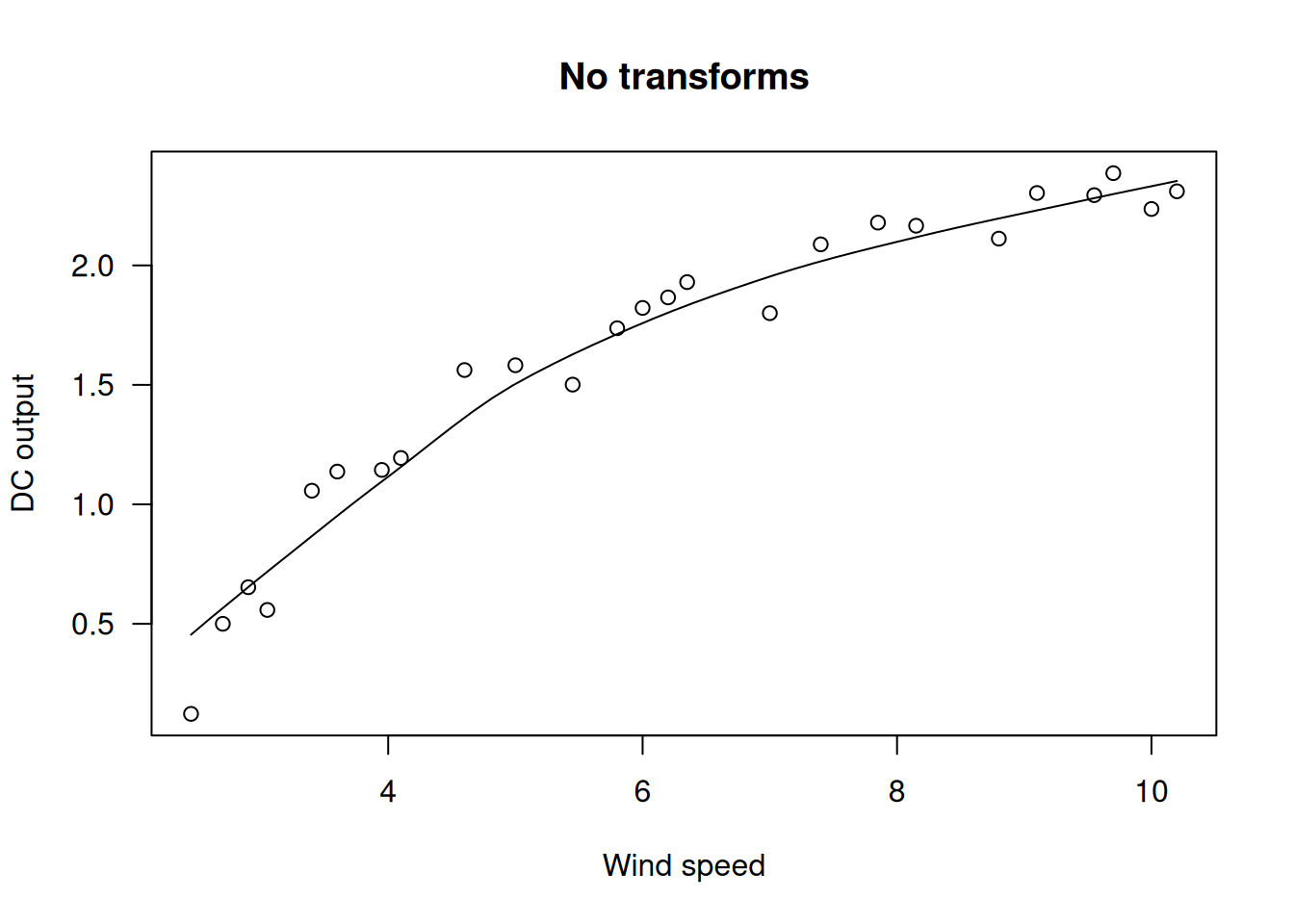
wm.m1 <- lm(DC ~ Wind, data=windmill)
scatter.smooth(rstandard(wm.m1) ~ fitted(wm.m1), main="No transforms",xlab="Standardized residuals", ylab="Fitted values", las=1)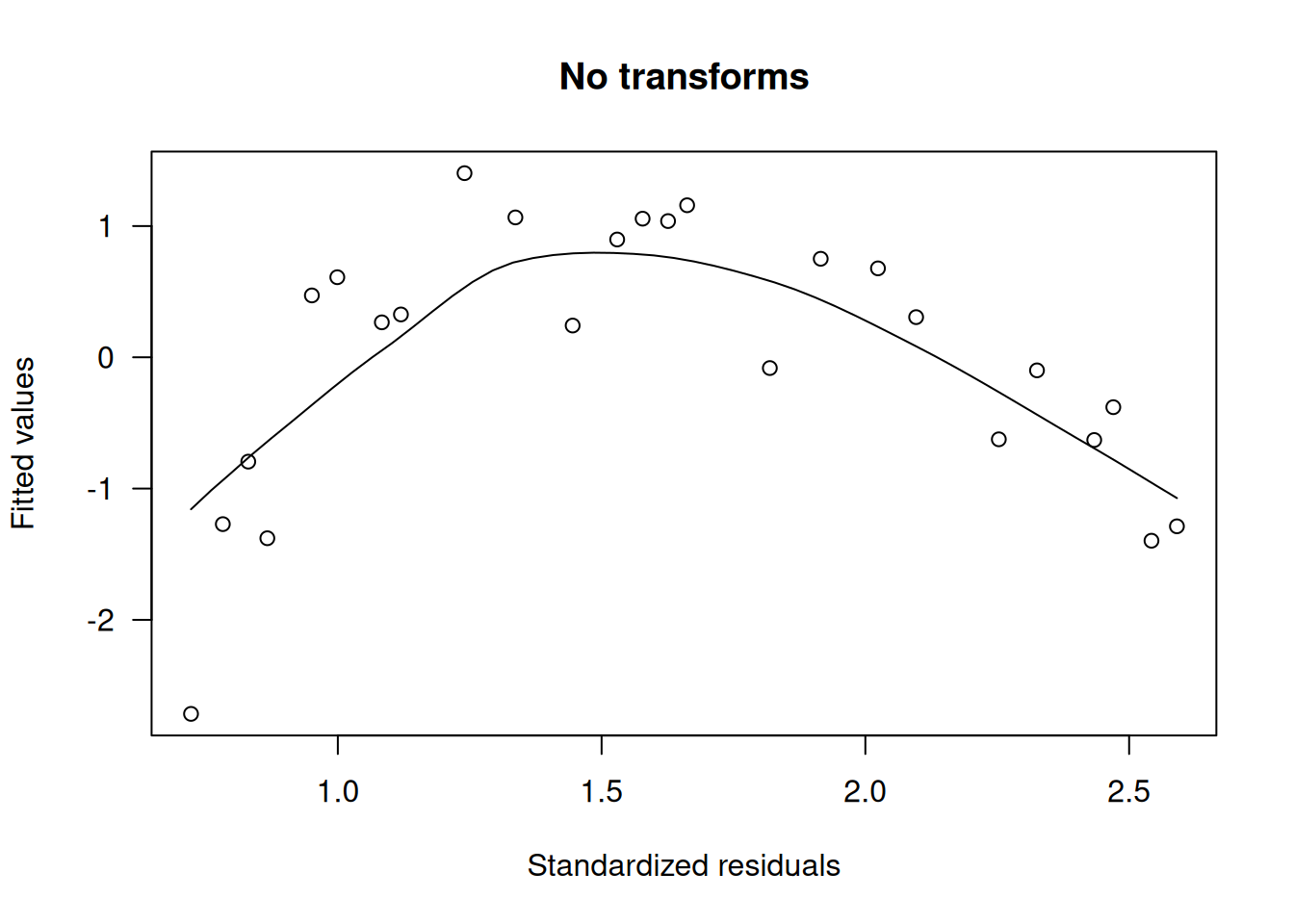
Para aliviar la no linealidad se prueban transformaciones de la covariable Wind
2.10.2.1 Transformación Logarítmica de Wind
scatter.smooth(windmill$DC ~ log(windmill$Wind), main="Log(Wind)", xlab="log(Wind speed)", ylab="DC output", las=1)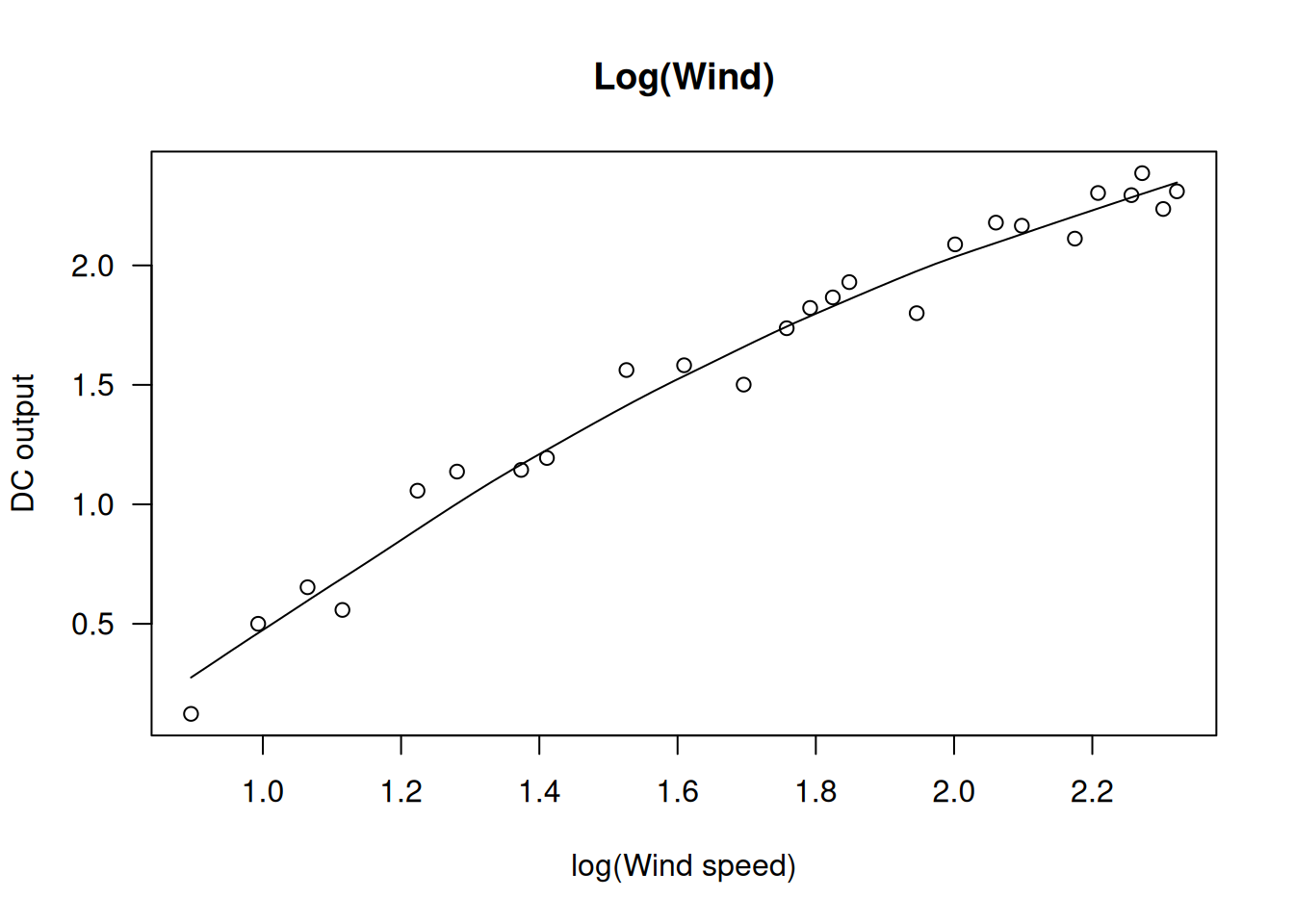
wm.m2 <- lm(DC ~ log(Wind), data=windmill)
scatter.smooth(rstandard(wm.m2) ~ fitted(wm.m2), main="Log(Wind)", ylab="Standardized residuals", xlab="Fitted values", las=1)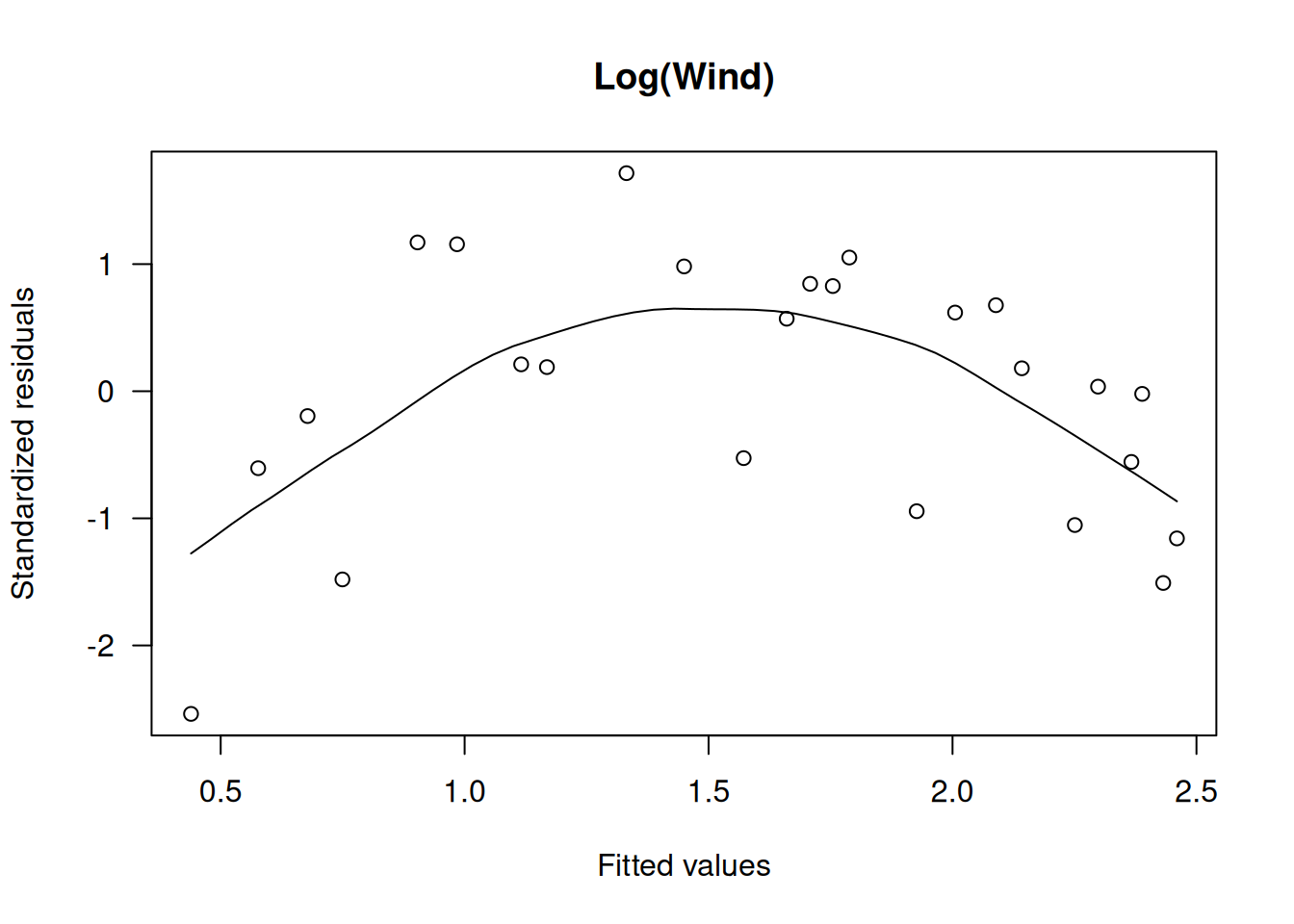
El gráfico con log(Wind) mejora la linealidad, pero aún puede haber cierta curvatura.
2.10.2.2 Transformación Recíproca de Wind
Dado que la transformación logarítmica no logra linealizar completamente la relación, se prueba una transformación recíproca:
scatter.smooth(windmill$DC ~ (1/windmill$Wind), main="1/Wind", xlab="1/(Wind speed)", ylab="DC output", las=1)
wm.m3 <- lm(DC ~ I(1/Wind), data=windmill)
scatter.smooth(rstandard(wm.m3) ~ fitted(wm.m3), main="1/Wind", ylab="Standardized residuals", xlab="Fitted values", las=1)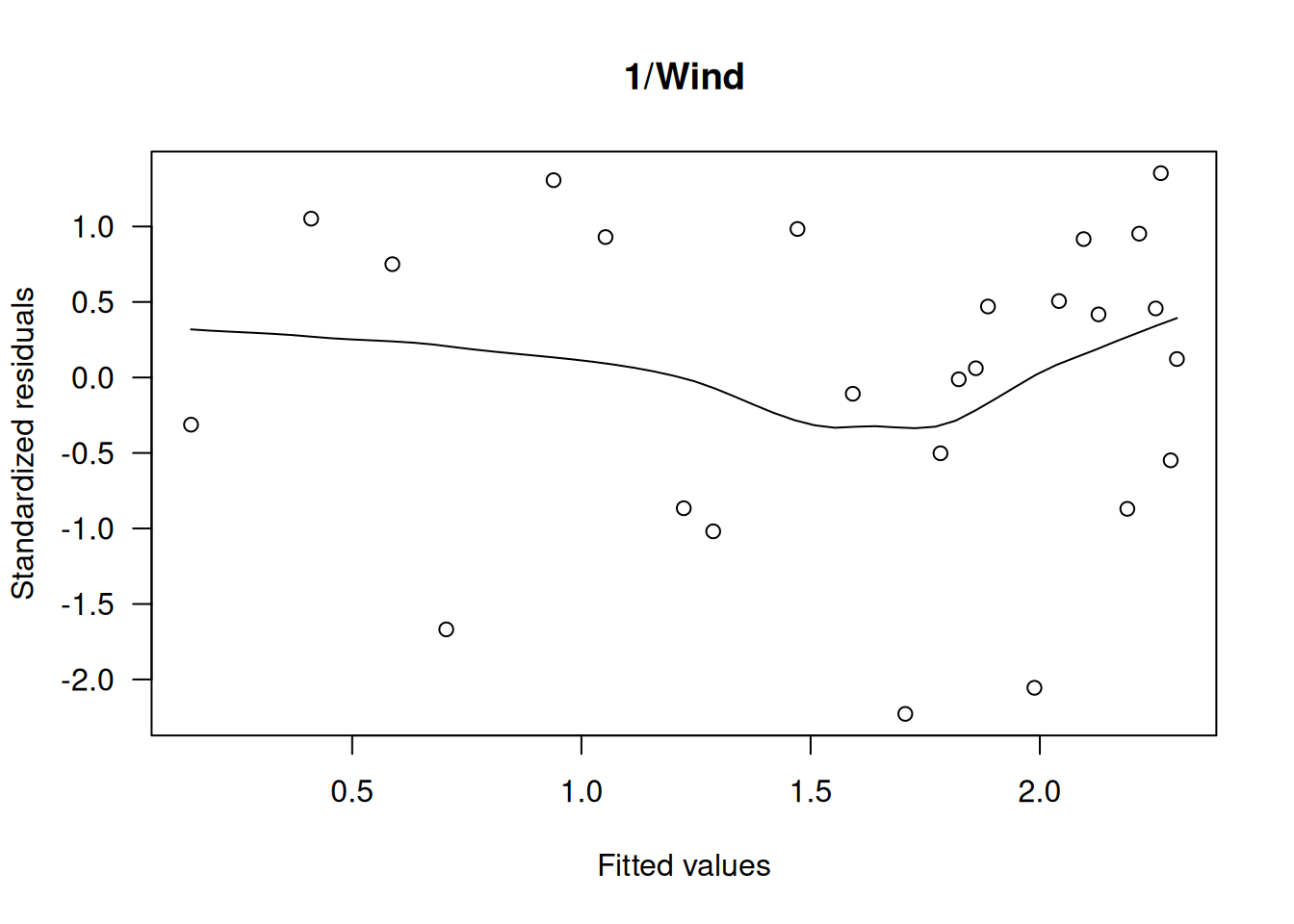
Nota: Se utiliza la función I() en la fórmula de lm() para asegurar que la expresión \(1/Wind\) se interprete aritméticamente y no como una parte de la fórmula.
Con la transformación recíproca, la relación se vuelve aproximadamente lineal y la varianza de los residuales se estabiliza, lo cual se confirma en los gráficos diagnósticos (por ejemplo, Cook’s distance y Q-Q plot).
2.10.3 Transformaciones Simultáneas de Covariables y Respuesta
En algunos casos, especialmente cuando se sospecha que las cantidades físicas se relacionan mediante leyes de potencia, puede ser útil transformar simultáneamente tanto \(x\) como \(y\).
Por ejemplo, si se supone que \(y\) es proporcional a una potencia de \(x\): \[
\mathrm{E}[y]=\alpha x^{\beta},
\] aplicar el logaritmo a ambas variables linealiza la relación: \[
\mathrm{E}[\log y] \approx \log \alpha + \beta \log x.
\]
2.10.3.1 Ejemplo: Relación entre FEV y Altura
En el estudio de capacidad pulmonar (data set: lungcap), FEV es una medida de volumen (en unidades cúbicas) y la altura está en unidades lineales. Se esperaría que el volumen sea proporcional a la altura al cubo. En la escala logarítmica, se ajusta el modelo:
LC.lm.log <- lm(log(FEV) ~ log(Ht), data=lungcap)
printCoefmat(coef(summary(LC.lm.log))) Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.921103 0.255768 -46.609 < 2.2e-16 ***
log(Ht) 3.124178 0.062232 50.202 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1plot(log(FEV) ~ log(Ht), data=lungcap, las=1)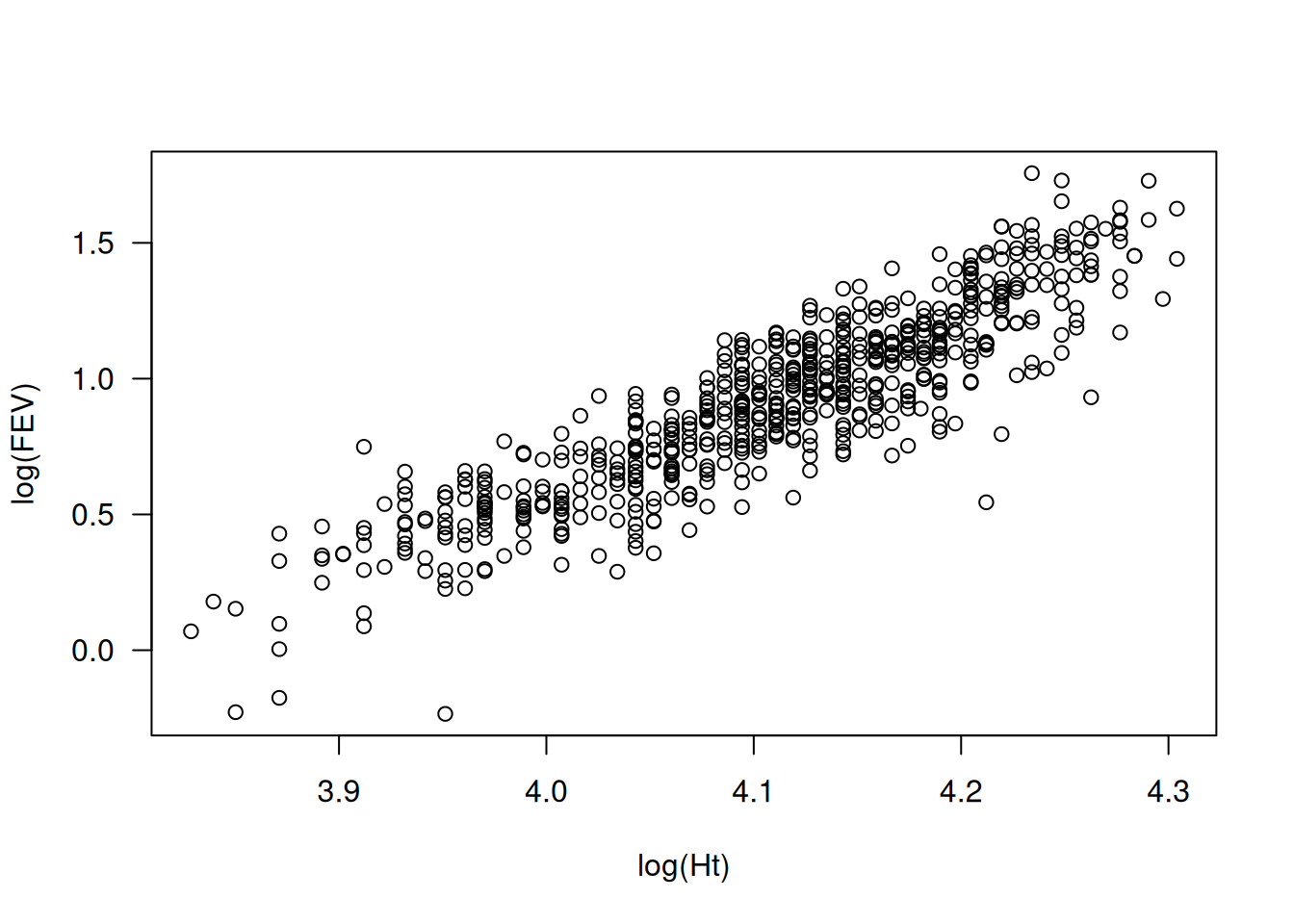
El resultado muestra una pendiente cerca de 3, lo cual es coherente con la relación esperada para un volumen proporcional a la altura al cubo.
2.10.3.2 Ejemplo: Datos de Árboles de Cereza
Se midió el volumen (\(y\)), la altura (\(h\)) y la circunferencia (girth, \(d\)) de 31 árboles de cereza. Se espera que el volumen de madera se relacione con la circunferencia y la altura.
Suponiendo que los árboles pueden aproximarse a conos o cilindros, se obtienen fórmulas teóricas: \[
\begin{aligned}
\text{Cono:} \quad & y = \frac{\pi (d/12)^2 h}{12}, \\
\text{Cilindro:} \quad & y = \frac{\pi (d/12)^2 h}{4}.
\end{aligned}
\] Al tomar logaritmos y simplificar, se llega a: \[
\begin{aligned}
\text{Cono:} \quad & \mu = \log(\pi/1728) + 2\log d + \log h, \\
\text{Cilindro:} \quad & \mu = \log(\pi/576) + 2\log d + \log h.
\end{aligned}
\] En lugar de imponer estos valores, se ajusta un modelo general: \[
\log \mu = \beta_0 + \beta_1 \log d + \beta_2 \log h.
\]
Se espera que \(\beta_1 \approx 2\) y \(\beta_2 \approx 1\), y el valor de \(\beta_0\) permita inferir si la forma del árbol se asemeja más a un cono o a un cilindro.
Para ajustar el modelo en R:
data(trees) # El data frame trees viene con R
m.trees <- lm(log(Volume) ~ log(Girth) + log(Height), data=trees)
printCoefmat(coef(summary(m.trees))) Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.631617 0.799790 -8.2917 5.057e-09 ***
log(Girth) 1.982650 0.075011 26.4316 < 2.2e-16 ***
log(Height) 1.117123 0.204437 5.4644 7.805e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1El valor estimado de \(\hat{\beta}_0=-6.632\) es cercano al valor esperado para un cono (\(\log(\pi/1728) \approx -6.310\)), mientras que \(\hat{\beta}_1\approx 2\) y \(\hat{\beta}_2\approx 1\), lo que confirma la relación teórica.
2.11 Colinealidad
La colinealidad, o multicolinealidad, ocurre cuando algunas de las covariables están altamente correlacionadas entre sí, lo que implica que miden casi la misma información. Esto significa que diferentes combinaciones de estas variables pueden producir valores ajustados casi idénticos. La colinealidad afecta principalmente la interpretación de los coeficientes (más que la predicción) y, en casos extremos, puede provocar problemas numéricos en el ajuste del modelo, aunque raramente ocurre con software moderno.
2.11.1 Consecuencias y Síntomas
Inflación de errores estándar:
Los coeficientes afectados por colinealidad tienen errores estándar elevados, lo que dificulta determinar la significación individual de cada covariable.Dependencia entre coeficientes:
Los coeficientes estimados dependen fuertemente de las demás variables incluidas en el modelo, haciendo casi imposible interpretar directamente el efecto de cada una.Múltiples soluciones:
Existen muchas combinaciones de covariables que producen predicciones similares, pero con coeficientes muy diferentes.
2.11.2 Detección de Colinealidad
Correlaciones entre covariables:
Una forma sencilla de detectar colinealidad es examinar la matriz de correlaciones entre las covariables. Correlaciones muy altas (cercanas a 1 o -1) son motivo de preocupación.Casos particulares:
Un ejemplo clásico es incluir una covariable y su cuadrado, como \(x\) y \(x^2\), que suelen estar altamente correlacionados. El uso de polinomios ortogonales o splines de regresión puede evitar este problema.
2.11.3 Soluciones frente a la Colinealidad
Si se detecta o sospecha colinealidad, algunas estrategias son:
Omisión de variables:
Retener únicamente las covariables con mayor sustento teórico o que sean más fáciles de medir, ya que las variables colineales contienen casi la misma información.Combinación de variables:
Por ejemplo, si la altura y el peso están altamente correlacionados, se puede usar el índice de masa corporal (BMI), definido como peso (kg) dividido por la altura (m) al cuadrado, en lugar de incluir ambas variables por separado.Recolección de más datos:
Si es posible, obtener observaciones que ayuden a distinguir mejor entre las covariables colineales.Métodos especiales:
Se pueden aplicar técnicas como la regresión ridge, aunque estos métodos están fuera del alcance de este curso.