7  GLMs: Diagnósticos

7.1 Supuestos de los GLMs

Al ajustar un modelo lineal generalizado (GLM) se toma como punto de partida una serie de supuestos que garantizan la validez de las inferencias y los contrastes. En primer lugar, se asume que no hay valores atípicos extremos: todas las observaciones provienen del mismo proceso generador y, por tanto, un único modelo es adecuado para el conjunto de datos.

El enlace \(g(\cdot)\) debe elegirse correctamente, de modo que la relación transformada entre la media \(\mu\) y el predictor lineal \(\eta\) sea apropiada. De igual forma, la linealidad prescribe que hemos incluido todas las variables explicativas relevantes y con la escala correcta en el predictor \(\eta=\beta_{0}+\sum \beta_{j}x_{j}\).

En lo que respecta a la varianza, el GLM postula una función de varianza \(V(\mu)\) conocida: cada distribución de la familia exponencial dispersa (EDM) impone una forma \(V(\mu)\) particular. Además, se requiere que la dispersión \(\phi\) sea constante en todas las observaciones.

La independencia de los \(y_i\) es otro pilar del modelo: cada respuesta debe ser generada sin depender de las demás. Implicándose en esto la suposición de que la distribución marginal de cada \(y_i\) pertenece a la familia EDM elegida.

Ninguno de estos supuestos es exacto en la práctica, por lo que después de ajustar el GLM es fundamental comprobar suposiciones mediante diagnóstico de residuos, pruebas de influencia y, cuando proceda, reformular el modelo (por ejemplo, cambiando el enlace, añadiendo variables o modelando la dispersión) para asegurar que las conclusiones sean robustas ante posibles desviaciones.

7.2 Residuos

7.2.1 Residuos en la respuesta son insuficientes para GLMs.

En regresión lineal clásica, los residuos se definen como la diferencia entre cada observación y su media predicha, \(y_i - \hat\mu_i\), y funcionan bien porque la varianza es constante. Sin embargo, en un GLM, la varianza de la respuesta suele depender de la media, de modo que dos observaciones con el mismo valor de \(y_i - \hat\mu_i\) pueden tener niveles muy diferentes de “extremidad” en su distribución ajustada.

Como ilustración, considere los datos de volumen de árboles de cerezo y el modelo gamma con enlace logarítmico,

library(GLMsData)
cherry.m1 <- glm(Volume ~ log(Girth) + log(Height),
                 family=Gamma(link="log"), data=trees)

En la Fig. 8.1 del Dunn se muestran dos observaciones, ambas con \(y_i - \hat\mu_i = 7\). La primera cae en la cola extrema de su distribución gamma ajustada, mientras que la segunda está en una zona de densidad aún notable. Sin cambiar la diferencia \(y_i - \hat\mu_i\), la probabilidad de cada valor difiere drásticamente, de modo que estos residuos no informan correctamente sobre la adecuación del modelo.

Por ello, en GLMs se buscan residuos que, tras una transformación adecuada, se comporten como residuos de regresión lineal: aproximadamente normales con media cero y varianza constante. Esto guía la definición de residuos deviance, Pearson y cuantílicos, que normalizan por la varianza ligada a la media y permiten diagnósticos válidos de ajuste.

7.2.2 Residuos de Pearson

Los residuos de Pearson escalan la diferencia entre la observación y el valor ajustado para homogeneizar la variabilidad. Se definen como

\[ r_{P}=\frac{y-\hat{\mu}}{\sqrt{V(\hat{\mu})/w}} \]

donde \(V(\cdot)\) es la función de varianza y \(w\) son los pesos previos. Estos residuos coinciden con los residuales ordinarios al interpretar el GLM como una regresión ponderada por respuestas y pesos de trabajo. Bajo las condiciones del Teorema del Límite Central, el estadístico de Pearson

\[ X^{2} \;=\;\sum r_{P}^{2} \]

sigue aproximadamente una \(\chi^{2}\) y cada \(r_{P}\) es casi normal centrado, lo que facilita la detección de observaciones atípicas y la evaluación de la adecuación del modelo.

Por ejemplo, para un modelo ajustado en R: resid(fit, type="pearson")

En distribuciones concretas, estos residuos toman formas sencillas. Para la normal, donde \(V(\mu)=1\),

\[ r_{P}=(y-\hat{\mu})\sqrt{w}\,, \]

y para la Poisson, donde \(V(\mu)=\mu\),

\[ r_{P}=\frac{y-\hat{\mu}}{\sqrt{\hat{\mu}/w}}\,. \]

Estos residuos ofrecen diagnósticos más fiables que los simples \(y_i-\hat\mu_i\), ya que homogeneizan la variabilidad a lo largo de todo el rango de \(\hat\mu_i\).

7.2.3 Residuos de devianza

Los residuos de Pearson homogeneizan la variabilidad dividiendo por \(\sqrt{V(\hat\mu)/w}\), pero no tienen en cuenta la forma completa de la función de verosimilitud. Para reflejar mejor la discrepancia entre la observación y el ajuste en el modelo, se definen los residuos de devianza como la raíz cuadrada con signo de la devianza unitaria:

\[ r_{D}=\operatorname{sign}(y-\hat{\mu}) \sqrt{w\,d(y, \hat{\mu})}\,. \tag{8.1} \]

Aquí, \(\operatorname{sign}(x)\) vale \(1\) si \(x>0\), \(-1\) si \(x<0\) y \(0\) si \(x=0\), y \(d(y,\hat\mu)\) es la devianza unitaria. En R, estos residuos se obtienen por defecto con:resid(fit)

Bajo las condiciones de la aproximación saddlepoint, la devianza total sigue aproximadamente una \(\chi^{2}\), y cada \(r_{D}\) queda casi normalmente distribuido. Esto permite detectar observaciones atípicas y evaluar la adecuación del modelo usando gráficos de residuos con referencia a la normalidad.

Por ejemplo, en distribuciones concretas los residuos toman formas sencillas:

• Normal (\(V(\mu)=1\)): \(r_{D}=(y-\hat{\mu})\sqrt{w}\,,\) que coincide con los residuos de Pearson en este caso.

• Poisson (\(V(\mu)=\mu\)):

  \[ r_{D}=\operatorname{sign}(y-\hat{\mu}) \sqrt{2w\Bigl\{y\log\bigl(\tfrac{y}{\hat\mu}\bigr)-(y-\hat\mu)\Bigr\}}\,. \]

7.2.4 Residuos cuantílicos

Los residuos de Pearson y de devianza pueden desviarse claramente de la normalidad cuando no se cumplen las pautas asintóticas, especialmente en distribuciones discretas. Para garantizar residuos con distribución exactamente normal (salvo la variabilidad por estimar \(\mu\) y \(\phi\)), se utilizan los residuos cuantílicos. Cada residuo cuantílico \(r_{Q}\) transforma la posición de la observación \(y\) en la escala de probabilidad de la distribución ajustada a la escala normal estándar.

Formalmente, si \(\mathcal{F}(y;\hat\mu,\phi)\) es la función de distribución acumulada (CDF) del EDM ajustado, entonces

\[ r_{Q}=\Phi^{-1}\bigl(\mathcal{F}(y;\hat\mu,\phi)\bigr)\,, \]

donde \(\Phi^{-1}\) es la inversa de la CDF normal estándar. Cuando \(\phi\) es desconocido, se sustituye por su estimador de Pearson.

Para distribuciones continuas, basta con evaluar directamente la CDF. Por ejemplo, en un EDM exponencial (\(\phi=1\)) con una observación \(y=1.2\) y \(\hat\mu=3\):

y <- 1.2; mu <- 3
cum.prob <- pexp(y, rate=1/mu)
rQ <- qnorm(cum.prob)
rQ

[1] -0.4407971

Nota: En distribuciones normales, se recupera el residuo de Pearson escalado por la desviación estándar:

\[ r_{Q}=\frac{(y-\hat\mu)\sqrt{w}}{s}\,. \]

Para EDM discretas, como la Poisson, se genera un valor aleatorio \(u\sim\mathrm{Uniform}(a,b]\) entre los saltos de la CDF en \(y\), donde \(a=\lim_{\epsilon\downarrow0}\mathcal{F}(y-\epsilon)\) y \(b=\mathcal{F}(y)\), y luego

\[ r_{Q}=\Phi^{-1}(u)\,. \]

Esta aleatorización hace que los residuos sean continuos y exactamente normales, a pesar de la discretización. En R, se obtienen con:

# library(statmod)
# qresid(fit)

Se recomienda generar varias réplicas de residuos cuantílicos en respuestas discretas para reducir el efecto de la aleatorización. Estos residuos son especialmente útiles en gráficos de diagnóstico, ya que mantienen la escala normal y permiten interpretar colas y tendencias de forma coherente.

Ejemplo

Para ilustrar la aleatorización necesaria en distribuciones discretas, consideremos un EDM de Poisson con una observación \(y=1\) y un valor ajustado \(\hat{\mu}=2.6\). La CDF de Poisson en \(y=1\) da un salto discreto entre

\[ a = \Pr(Y \le 0) = 0.07427358,\quad b = \Pr(Y \le 1) = 0.26738488. \]

Seleccionamos un punto uniforme \(u\sim\mathrm{Uniform}(a,b]\) y luego transformamos a la escala normal:

set.seed(123)
y <- 1; mu <- 2.6
a <- ppois(y-1, mu)    # 0.07427358
b <- ppois(y,   mu)    # 0.26738488
u <- runif(1, a, b)    
rq <- qnorm(u)         
rq

[1] -1.127299

Si, $u$ y

\[ r_{Q} = \Phi^{-1}(u) \approx -1.1273. \]

Este residuo cuantílico refleja correctamente que la probabilidad acumulada hasta \(y=1\) está en la cola izquierda de la distribución Poisson ajustada, proporcionando un diagnóstico más coherente que el simple \(y-\hat\mu=1-2.6=-1.6\).

7.3 Los apalancamientos en GLMs

7.3.1 Apalancamientos de trabajo

En GLMs, la estimación de los coeficientes mediante IRLS muestra que localmente el modelo se comporta como una regresión lineal ponderada con respuestas de trabajo \(z_{i}\) y pesos de trabajo \(W_{i}\). Si tratamos estos valores como fijos, podemos definir el apalancamiento \(h_{i}\) de cada observación exactamente igual que en regresión lineal: es la proporción de peso que el ajuste concede a \(z_{i}\) al estimar el predictor lineal \(\hat{\eta}_{i}\). Valores pequeños de \(h_{i}\) indican que el ajuste incorpora información de muchas observaciones, mientras que \(h_{i}=1\) implica que \(\hat{\eta}_{i}=z_{i}\) y por tanto \(\hat{\mu}_{i}=y_{i}\), es decir, el punto domina el ajuste.

La varianza aproximada del residual de trabajo \(e_{i}=z_{i}-\hat{\eta}_{i}\) viene dada por

\[ \operatorname{var}\bigl[e_{i}\bigr]\approx \phi\,V\bigl(\hat{\mu}_{i}\bigr)\,\bigl(1-h_{i}\bigr)\,, \]

donde \(V(\cdot)\) es la función de varianza del EDM y \(\phi\) puede reemplazarse por un estimador adecuado cuando sea desconocida. En R, los apalancamientos se obtienen con hatvalues().

7.3.2 La matriz de proyección (Hat Matrix)

El hat matrix generaliza la matriz de proyección de la regresión lineal al caso de GLMs mediante los pesos finales de IRLS. Se define como

\[ \mathrm{H}=\mathrm{W}^{1/2}\,X\bigl(X^{T}WX\bigr)^{-1}X^{T}\mathrm{W}^{1/2}\,, \]

donde \(W\) es la matriz diagonal de pesos \(W_{i}\) evaluados en la solución. Las diagonales de \(\mathrm{H}\) son precisamente los apalancamientos \(h_{i}\), que en R se calculan también con hatvalues(). Este enfoque mantiene la misma interpretación geométrica de la regresión lineal, adaptada a la variabilidad dependiente de la media propia de los GLMs.

7.4 Residuos estandarizados con apalancamiento en GLMs

En GLMs, los residuos crudos (Pearson, devianza y cuantílicos) pueden presentar varianzas que dependen de la media ajustada. Para homogeneizar esta variabilidad se definen los residuos estandarizados, dividiendo cada tipo de residuo por \(\sqrt{1-h_i}\) (y por \(\sqrt{\phi}\) cuando procede). Con \(h\) denotando el apalancamiento, las definiciones son

\[ \begin{align*} r_{P}^{\prime} & =\frac{r_{P}}{\sqrt{\phi(1-h)}}=\frac{y-\hat{\mu}}{\sqrt{\phi\,V(\hat{\mu})\,(1-h)/w}} \\ r_{D}^{\prime} & =\frac{r_{D}}{\sqrt{\phi(1-h)}}=\frac{\operatorname{sign}(y-\hat{\mu}) \sqrt{w\,d(y, \hat{\mu})}}{\sqrt{\phi(1-h)}} \\ r_{Q}^{\prime} & =\frac{r_{Q}}{\sqrt{1-h}}\,, \end{align*} \]

donde \(V(\mu)\) es la función de varianza del EDM y \(d(y,\mu)\) la devianza unitaria. Cuando \(\phi\) es desconocida, R emplea por defecto el estimador de Pearson \(\bar\phi\).

Los residuos de deviance estandarizados pueden obtenerse directamente con rstandard(fit). Para los residuos Pearson y cuantiles hay que calcularlos manualmente usando las fórmulas anteriores y los valores de resid(fit, type="pearson"), qresid(fit) y hatvalues(fit).

Los residuos estandarizados tienen varianza aproximadamente constante y permiten diagnosticar mejor puntos influentes o atípicos. Además, \(r_{D}'^{2}\) se interpreta como la reducción aproximada en la devianza residual al omitir la observación \(i\), escalada por \(\phi\).

Ejemplo

Ajustamos un GLM gamma a los datos de los cerezos y comparamos los tres tipos de residuos crudos y estandarizados:

library(statmod)            # Para qresid()
fit <- glm(Volume ~ log(Girth) + log(Height),
           family=Gamma(link="log"), data=trees)

# Residuos crudos
rP <- resid(fit, type="pearson")
rD <- resid(fit)           # Deviance por defecto
rQ <- qresid(fit)

# Estimador de dispersion
phi.est <- summary(fit)$dispersion

# Apalancamientos
h <- hatvalues(fit)

# Residuos estandarizados
rP.std <- rP / sqrt(phi.est * (1 - h))
rD.std <- rstandard(fit)
rQ.std <- rQ / sqrt(1 - h)

# Primeras seis observaciones
all.res <- cbind(rP, rP.std, rD, rD.std, rQ, rQ.std)
head(all.res)

           rP     rP.std          rD     rD.std         rQ     rQ.std
1  0.01935248  0.2620392  0.01922903  0.2603676  0.2665369  0.2893348
2  0.03334904  0.4558288  0.03298537  0.4508579  0.4380951  0.4800656
3  0.01300934  0.1811459  0.01295335  0.1803663  0.1882715  0.2101705
4 -0.01315583 -0.1691519 -0.01321397 -0.1698994 -0.1380666 -0.1423184
5 -0.04635977 -0.6169148 -0.04709620 -0.6267146 -0.5606192 -0.5980889
6 -0.04568564 -0.6188416 -0.04640051 -0.6285250 -0.5519432 -0.5993880

Al inspeccionar apply(all.res, 2, var), comprobamos que las varianzas de los residuos estandarizados son cercanas a uno, confirmando su papel en el diagnóstico de ajuste.

apply(all.res, 2, var)

         rP      rP.std          rD      rD.std          rQ      rQ.std 
0.005998800 1.013173741 0.006113175 1.032103295 0.950789672 1.031780512 

Cuándo usar cada tipo de residuo

En modelos lineales generalizados, los residuos de Pearson, devianza y cuantílicos coinciden en tener distribución normal exacta cuando la familia es normal (y también devianza exacta para gaussiana inversa), salvo por la variabilidad en \(\hat\mu\) y \(\hat\phi\). Sin embargo, para muchas distribuciones discretas de la familia EDM, ni los residuos de Pearson ni los de devianza garantizan estar próximos a la normalidad; aquí entran en juego las reglas asintóticas del CLT y Saddlepoint para evaluar cuándo las aproximaciones asintóticas son confiables.

Para distribuciones discretas, los residuos cuantilicos son particularmente recomendables, ya que evitan los patrones artificiales que pueden surgir con Pearson o deviance. En todos los casos, estandarizar o “studentizar” los residuos mejora la homogeneidad de la varianza y facilita la detección de observaciones influyentes.

Por último, en diagnósticos específicos pueden emplearse variantes como los residuos parciales o de trabajo (Sect. 8.7.3), que aportan información adicional sobre la forma funcional de los efectos de las covariables.

7.5 Verificación de Supuestos

7.5.1 Independencia: graficar residuos frente a residuos rezagados

La independencia de las respuestas es la suposición más crítica en un GLM, habitualmente garantizada por el diseño del estudio. No obstante, cuando los datos se recogen en serie temporal, podemos evaluar la independencia inspeccionando visualmente si existe dependencia temporal en los residuos. Para ello, se grafica cada residuo frente al residuo inmediatamente anterior en el tiempo; bajo independencia, el diagrama de dispersión no muestra patrones sistemáticos. De manera análoga, si los datos son espaciales, bastará con trazar los residuos frente a coordenadas geográficas (por ejemplo, latitud y longitud) o frente a cualquier covariable espacial relevante, buscando ausencia de tendencia o agrupamiento.

Este procedimiento es análogo al usado en regresión lineal, y sirve como diagnóstico sencillo para detectar autocorrelación temporal o espacial en los residuos.

7.5.2 Gráficos para Verificar el Componente Sistemático

Para asegurar que la parte sistemática de un GLM está bien especificada, se examinan gráficos de residuos frente a los valores ajustados \(\hat\mu\) y frente a cada covariable \(x_j\). Dado que los residuos ordinarios pueden mostrar varianza no constante, se prefieren los residuos de desvianza estandarizados o los residuos de cuantiles, especialmente en distribuciones discretas, donde los patrones en residuos de Pearson o desvianza pueden resultar confusos.

En estos gráficos, dos aspectos son esenciales. Primero, la aparición de tendencias —una curva o pendiente en el diagrama— indica que la forma del predictor lineal o la función de enlace puede no ser adecuada, o que faltan variables o transformaciones de covariables. Segundo, la variación constante de los puntos sugiere que la función de varianza utilizada en el modelo es correcta.

Cuando \(\hat\mu\) se concentra en un rango un tanto estrecho, conviene graficar en la escala de información constante (transformación estabilizadora de varianza)con el fin de facilitar la detección de tendencias:

EDM	Escala de información constante
Binomial	\(\sin^{-1}\sqrt{\hat\mu}\)
Poisson	\(\sqrt{\hat\mu}\)
Gamma	\(\log\hat\mu\)

Un paso adicional para chequear la función de enlace es graficar las respuestas de trabajo
\[ z_i = \hat\eta_i + \frac{d\eta_i}{d\mu_i}(y_i - \hat\mu_i) \]
frente a \(\hat\eta_i\). Si la enlace \(g(\cdot)\) es apropiada, el diagrama debe aproximarse a la línea de igualdad.

Por último, los residuos parciales
\[ u_{j,i} = e_i + \hat\beta_j\,x_{j,i} \]
permiten evaluar si cada covariable aparece en la escala correcta. Un gráfico de \(u_{j,i}\) versus \(x_{j,i}\) (component-plus-residual plot) debe revelar una relación lineal si \(x_j\) está bien transformada. En R, puede usarse:

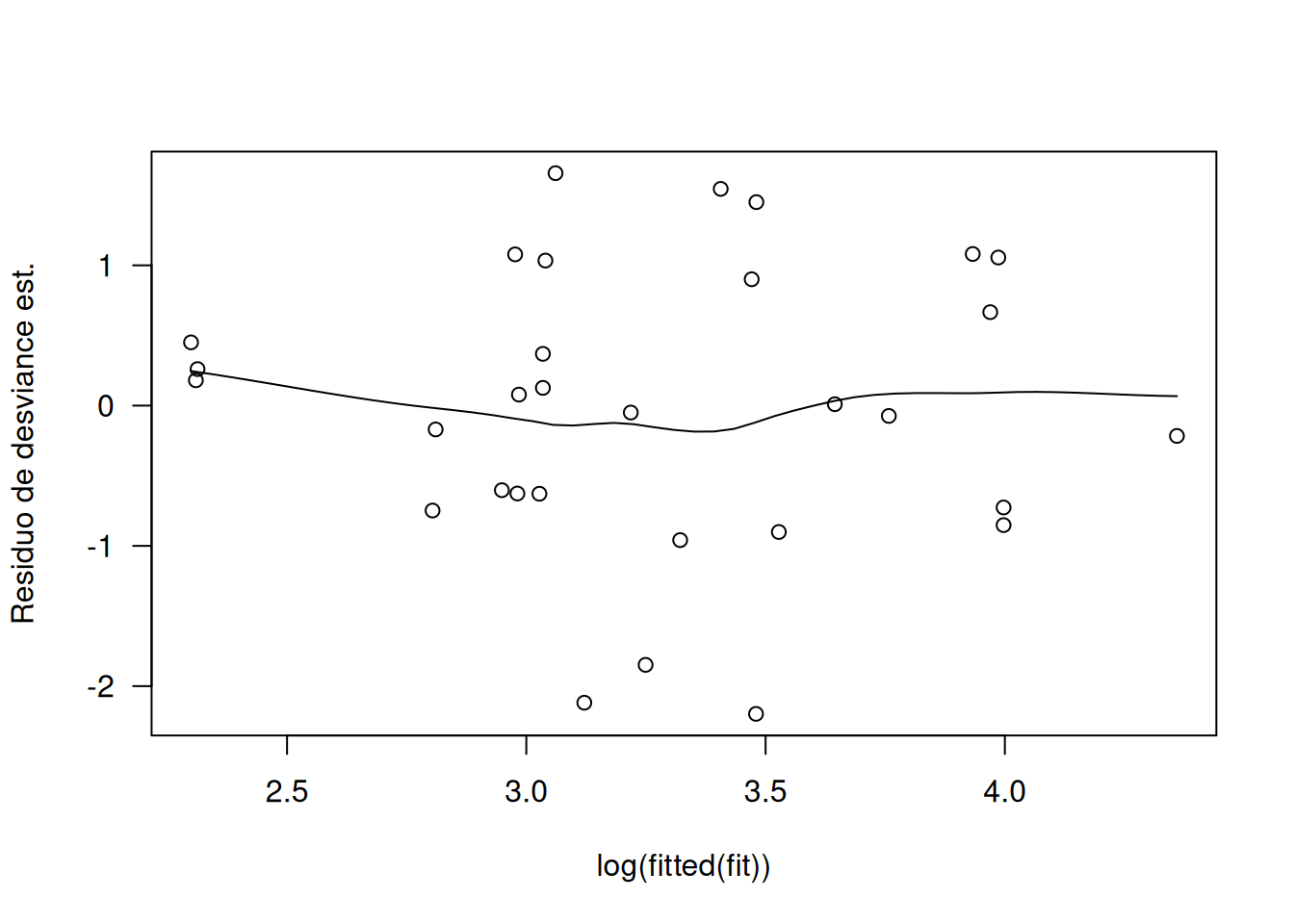
# Residuos de desviance estandarizados frente a log(fitted)
scatter.smooth(
  rstandard(fit) ~ log(fitted(fit)),
  las=1, ylab="Residuo de desviance est."
)

# Respuesta de trabajo vs predictor lineal
z <- resid(fit, type="working") + fit$linear.predictor
plot(
  z ~ fit$linear.predictor,
  las=1,
  xlab="Predictor lineal",
  ylab="Respuesta de trabajo"
)
abline(0, 1)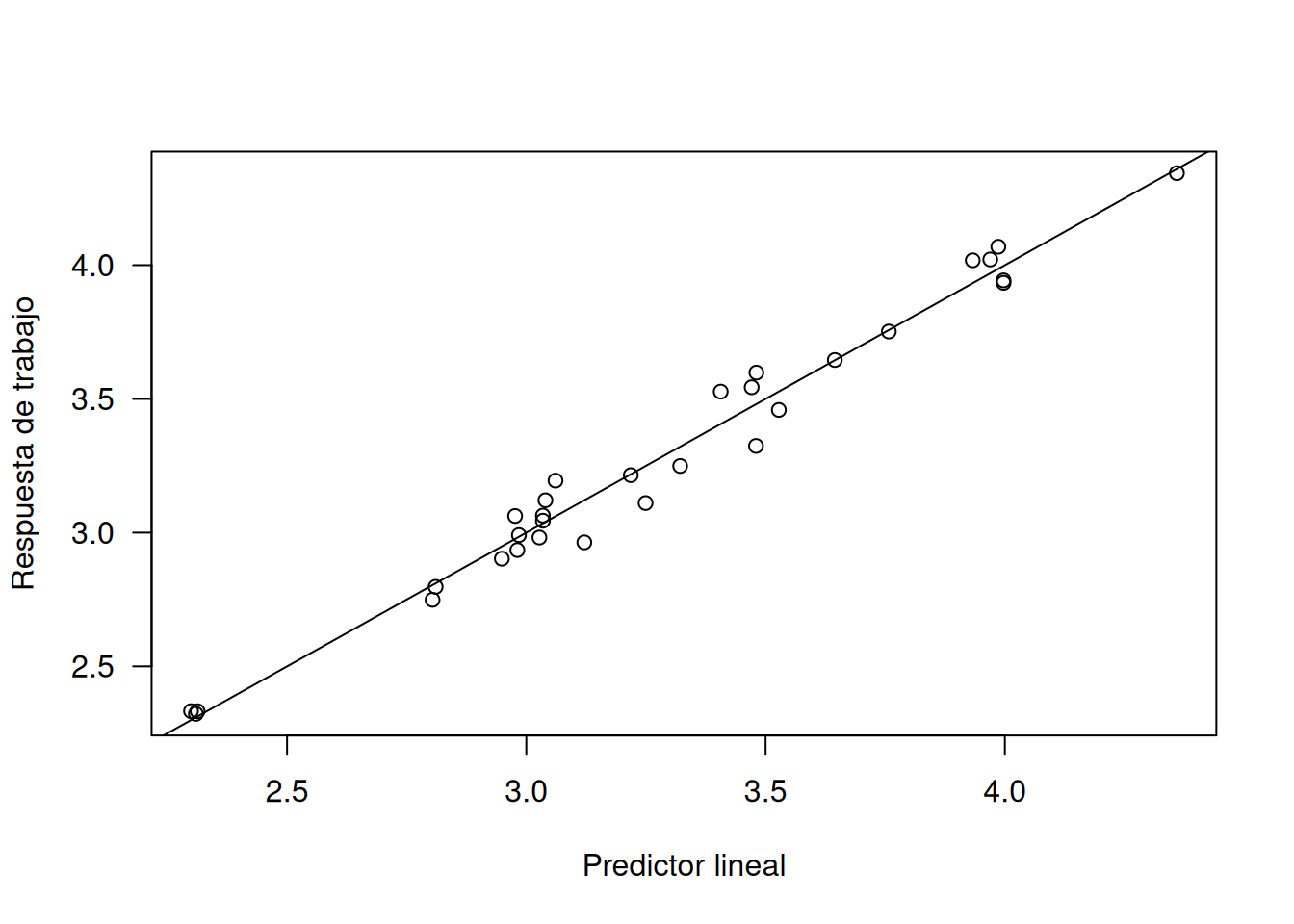

# Residuos parciales
termplot(fit, partial.resid=TRUE, las=1)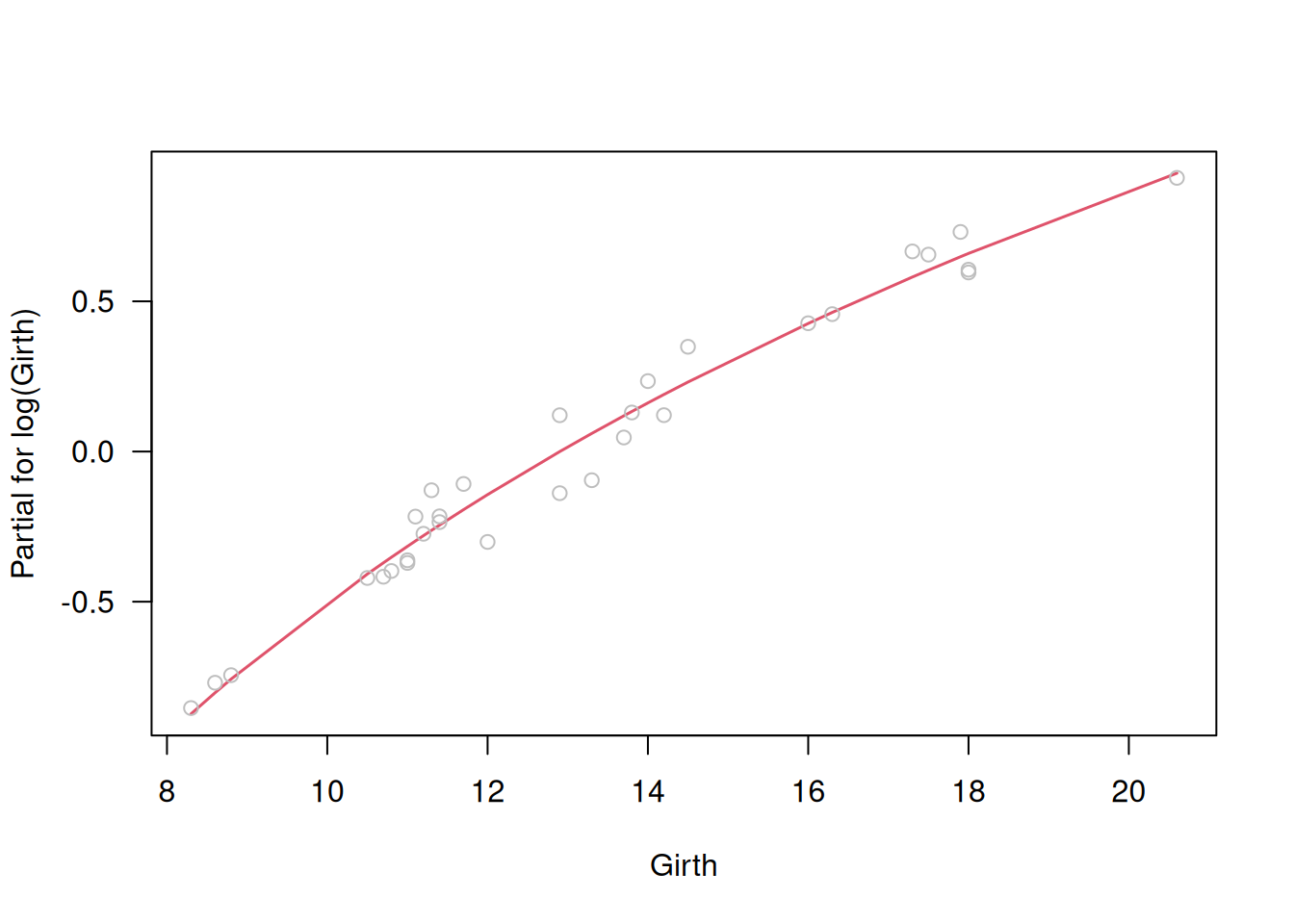

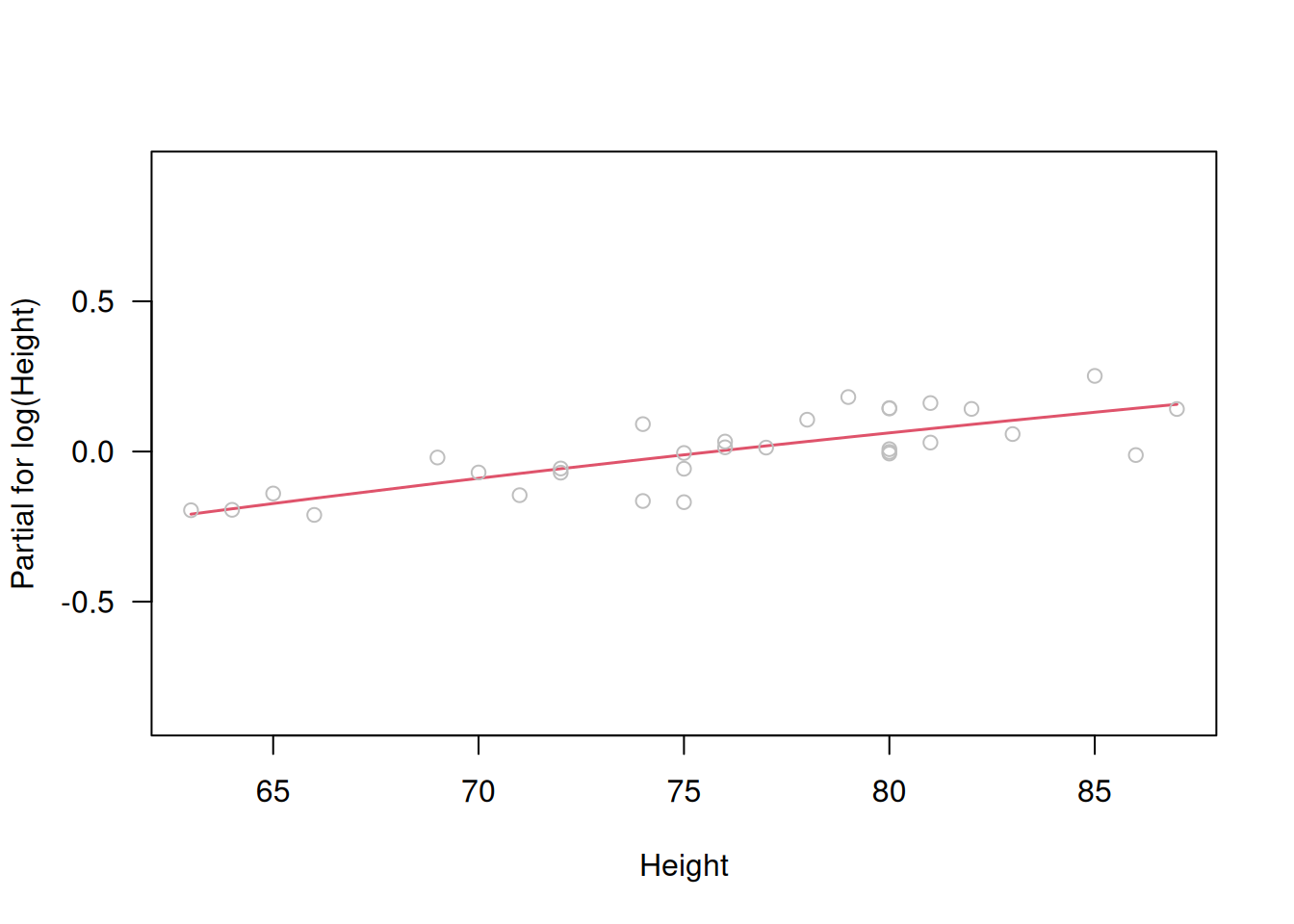
Estos diagnósticos visuales ayudan a detectar enlaces mal elegidos, transformaciones de covariables inadecuadas o la necesidad de incluir términos adicionales en el modelo.

7.5.3 Verificación de la Componente Aleatoria mediante Gráficos

La especificación correcta de la distribución de la respuesta en un GLM suele basarse en el tipo de datos (por ejemplo, binomial para proporciones, Poisson para recuentos). No obstante, es útil confirmar esta elección examinando un gráfico Q–Q de los residuos de cuantiles, ya que éstos siguen exactamente una distribución normal estándar (aparte de la variabilidad en la estimación de \(\mu\) y \(\phi\)) siempre que el modelo EDM sea el adecuado.

En R, tras ajustar un modelo como cherry.m1 (GLM gamma con enlace log) a los datos de volumen de los cerezos, se obtienen y grafican los residuos de cuantiles así:

qr.cherry <- qresid(cherry.m1)
qqnorm(qr.cherry, las=1)
qqline(qr.cherry)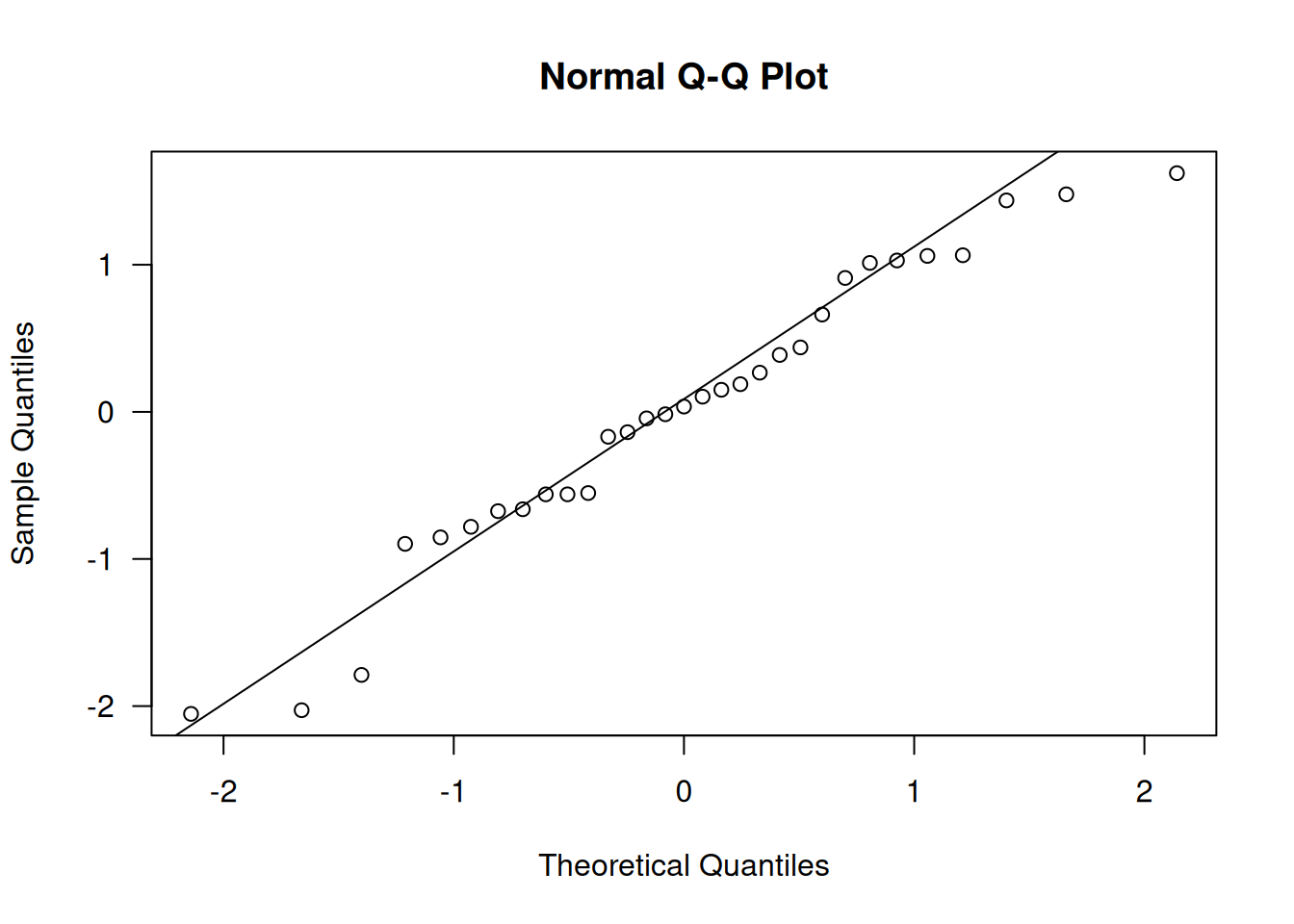

En la figura anterior, los puntos siguen de cerca la línea de identidad, lo que indica que el supuesto de una distribución gamma es razonable para estos datos.

7.6 Outliers y observaciones influyentes

7.6.1 Valores Atípicos y Residuos Estudentizados

Detectar observaciones atípicas en un GLM pasa por identificar residuos inusualmente grandes (positivos o negativos). Aunque los residuos de devianza estandarizados suelen emplearse para ello, en datos discretos resulta más fiable usar residuos de cuantiles. Una mejora adicional consiste en “studentizar” los residuos de devianza, es decir, ajustar cada residual según la influencia de su propia observación sin necesidad de volver a ajustar el modelo \(n\) veces.

Los residuos de devianza studentizados aproximados se definen como

\[ r_{i}'' = \operatorname{sign}(y_{i}-\hat\mu_{i})\sqrt{\frac{1}{\phi}\Bigl(r_{D,i}^{2} + \frac{h_{i}}{1-h_{i}}\,r_{P,i}^{2}\Bigr)}\,, \]

donde \(r_{D,i}\) y \(r_{P,i}\) son los residuos de devianza y de Pearson, y \(h_{i}\) el apalancamiento de la observación \(i\). Si \(\phi\) es desconocido, se estima mediante

\[ \bar\phi_{(i)} \approx \frac{D(y,\hat\mu) - r_{D,i}^{2}/(1-h_{i})}{n-p'-1}\,, \]

simulando el estimador de media de devianza sin la observación \(i\). En R, estos residuos se obtienen directamente con rstudent().

library(statmod)  # Para qresid()
# Calcular distintos residuos para el modelo cherry.m1
rs <- cbind(
  rD    = resid(cherry.m1),        # deviance residuals
  rDstd = rstandard(cherry.m1),    # standardized deviance residuals
  rDstu = rstudent(cherry.m1),     # studentized deviance residuals
  rQ    = qresid(cherry.m1)        # quantile residuals
)
head(rs)

           rD      rDstd      rDstu         rQ
1  0.01922903  0.2603676  0.2537382  0.2665369
2  0.03298537  0.4508579  0.4408129  0.4380951
3  0.01295335  0.1803663  0.1756442  0.1882715
4 -0.01321397 -0.1698994 -0.1652566 -0.1380666
5 -0.04709620 -0.6267146 -0.6125166 -0.5606192
6 -0.04640051 -0.6285250 -0.6140386 -0.5519432

apply(abs(rs), 2, max)  # Máximo valor absoluto de cada columna

      rD    rDstd    rDstu       rQ 
0.166763 2.197761 2.329122 2.053011 

En este ejemplo (datos de árboles de cerezo), como la dispersión \(\phi\) es pequeña, los residuos de cuantiles, devianza estandarizados y studentizados toman valores semejantes, y ninguno supera niveles que sugieran un outlier.

7.6.2 Observaciones Influyentes

Las observaciones influyentes combinan residuos grandes con alto apalancamiento, de modo que tienen un efecto desproporcionado en los parámetros del modelo. En GLMs se adaptan las medidas clásicas de regresión lineal usando los resultados de la última iteración de IRLS.

Una aproximación a la distancia de Cook para GLMs es:

\[ \begin{equation*} D \approx \left(\frac{r_{P}}{1-h}\right)^{2}\,\frac{h}{\phi\,p'} \;=\;\frac{\bigl(r_{P}^{\prime}\bigr)^{2}}{p'}\,\frac{h}{1-h} \tag{8.5} \end{equation*} \]

donde \(r_P'\) es el residuo de Pearson estandarizado, \(h\) la apalancamiento, \(\phi\) la dispersión y \(p'\) el número de parámetros. Las otras medidas (DFBETAS, DFFITS, razón de covarianza) se calculan con las mismas fórmulas que en regresión lineal, sustituyendo \(s^2_{(i)}\) por la dispersión sin la observación \(i\).

En R se disponen de:

cooks.distance(fit)

           1            2            3            4            5            6 
4.082875e-03 1.390620e-02 2.692504e-03 5.964593e-04 1.752456e-02 2.288955e-02 
           7            8            9           10           11           12 
2.436267e-02 6.264727e-03 3.742581e-02 1.003986e-04 7.746218e-02 2.609472e-04 
          13           14           15           16           17           18 
2.251272e-03 3.211862e-02 4.929254e-02 3.815356e-02 1.131422e-01 2.067211e-01 
          19           20           21           22           23           24 
2.233518e-02 2.614032e-04 1.104597e-02 1.247802e-02 4.304539e-02 4.252042e-06 
          25           26           27           28           29           30 
1.374721e-04 3.844647e-02 1.542758e-02 4.269362e-02 1.896139e-02 2.592849e-02 
          31 
3.393537e-03 

dffits(fit)

           1            2            3            4            5            6 
 0.107063194  0.197157785  0.087070844 -0.041337603 -0.228084738 -0.260619748 
           7            8            9           10           11           12 
-0.270561222 -0.136301487  0.323537296  0.016843881  0.472711919  0.027126045 
          13           14           15           16           17           18 
 0.079341475  0.299818426 -0.430929283 -0.368286550  0.569507539 -0.888248207 
          19           20           21           22           23           24 
-0.262310375 -0.027264309  0.175423110 -0.195447323  0.349773356  0.003472252 
          25           26           27           28           29           30 
-0.019787594  0.328100566  0.207316095  0.345693495 -0.238471672 -0.280757969 
          31 
-0.098713794 

dfbetas(fit)

    (Intercept)   log(Girth)  log(Height)
1   0.015408630 -0.083009418  0.004885819
2   0.120331353 -0.082080808 -0.089559644
3   0.065387206 -0.021045790 -0.053970180
4  -0.010535573  0.020869255  0.004494020
5   0.145191350  0.171498882 -0.170395141
6   0.186329347  0.191066170 -0.211870708
7  -0.227554383 -0.028403323  0.209562548
8   0.014348863  0.081148023 -0.032366233
9  -0.192892961 -0.227370714  0.226882604
10 -0.001401350 -0.009171148  0.003487508
11 -0.251405000 -0.313891410  0.300576530
12 -0.005647786 -0.014946534  0.008720768
13 -0.016519315 -0.043717396  0.025507536
14  0.223492415  0.037726025 -0.206936290
15 -0.009381538  0.122853472 -0.024937772
16 -0.117474524 -0.060001427  0.113427353
17 -0.468452807 -0.256817268  0.484161343
18  0.751122782  0.354148575 -0.763308331
19 -0.178216132 -0.138998137  0.188342996
20 -0.024279071 -0.015840728  0.025220873
21 -0.039038694  0.032669971  0.030898236
22  0.091760684 -0.014033480 -0.082616820
23  0.147020283  0.208728098 -0.173706633
24  0.002015469  0.002727174 -0.002383047
25 -0.002765934 -0.014372994  0.005396763
26 -0.076639235  0.202990436  0.028601961
27 -0.064934158  0.119966774  0.034724908
28 -0.029612012  0.252386459 -0.024682940
29  0.018846835 -0.175897082  0.018871525
30  0.022188795 -0.207087522  0.022217863
31  0.043759605 -0.057329529 -0.027820651

covratio(fit)

        1         2         3         4         5         6         7         8 
1.3048855 1.3108062 1.3850704 1.1814346 1.2176748 1.2614147 1.1935266 1.1304474 
        9        10        11        12        13        14        15        16 
1.0937971 1.1688650 0.8874669 1.1675827 1.1528938 1.0617893 0.6924645 0.7890128 
       17        18        19        20        21        22        23        24 
0.9712780 0.7314189 1.0883773 1.4724561 1.0627104 1.0722730 0.9368907 1.2594373 
       25        26        27        28        29        30        31 
1.1997311 1.0758495 1.1713549 1.0975152 1.1725721 1.1478297 1.3539299 

influence.measures(fit)

Influence measures of
     glm(formula = Volume ~ log(Girth) + log(Height), family = Gamma(link = "log"),      data = trees) :

     dfb.1_ dfb.l.G. dfb.l.H.    dffit cov.r   cook.d    hat inf
1   0.01541 -0.08301  0.00489  0.10706 1.305 4.08e-03 0.1514    
2   0.12033 -0.08208 -0.08956  0.19716 1.311 1.39e-02 0.1672    
3   0.06539 -0.02105 -0.05397  0.08707 1.385 2.69e-03 0.1975   *
4  -0.01054  0.02087  0.00449 -0.04134 1.181 5.96e-04 0.0589    
5   0.14519  0.17150 -0.17040 -0.22808 1.218 1.75e-02 0.1214    
6   0.18633  0.19107 -0.21187 -0.26062 1.261 2.29e-02 0.1520    
7  -0.22755 -0.02840  0.20956 -0.27056 1.194 2.44e-02 0.1194    
8   0.01435  0.08115 -0.03237 -0.13630 1.130 6.26e-03 0.0506    
9  -0.19289 -0.22737  0.22688  0.32354 1.094 3.74e-02 0.0906    
10 -0.00140 -0.00917  0.00349  0.01684 1.169 1.00e-04 0.0465    
11 -0.25140 -0.31389  0.30058  0.47271 0.887 7.75e-02 0.0722    
12 -0.00565 -0.01495  0.00872  0.02713 1.168 2.61e-04 0.0464    
13 -0.01652 -0.04372  0.02551  0.07934 1.153 2.25e-03 0.0464    
14  0.22349  0.03773 -0.20694  0.29982 1.062 3.21e-02 0.0727    
15 -0.00938  0.12285 -0.02494 -0.43093 0.692 4.93e-02 0.0356    
16 -0.11747 -0.06000  0.11343 -0.36829 0.789 3.82e-02 0.0356    
17 -0.46845 -0.25682  0.48416  0.56951 0.971 1.13e-01 0.1163    
18  0.75112  0.35415 -0.76331 -0.88825 0.731 2.07e-01 0.1255    
19 -0.17822 -0.13900  0.18834 -0.26231 1.088 2.23e-02 0.0711    
20 -0.02428 -0.01584  0.02522 -0.02726 1.472 2.61e-04 0.2428   *
21 -0.03904  0.03267  0.03090  0.17542 1.063 1.10e-02 0.0375    
22  0.09176 -0.01403 -0.08262 -0.19545 1.072 1.25e-02 0.0461    
23  0.14702  0.20873 -0.17371  0.34977 0.937 4.30e-02 0.0539    
24  0.00202  0.00273 -0.00238  0.00347 1.259 4.25e-06 0.1145    
25 -0.00277 -0.01437  0.00540 -0.01979 1.200 1.37e-04 0.0709    
26 -0.07664  0.20299  0.02860  0.32810 1.076 3.84e-02 0.0855    
27 -0.06493  0.11997  0.03472  0.20732 1.171 1.54e-02 0.0916    
28 -0.02961  0.25239 -0.02468  0.34569 1.098 4.27e-02 0.0982    
29  0.01885 -0.17590  0.01887 -0.23847 1.173 1.90e-02 0.1006    
30  0.02219 -0.20709  0.02222 -0.28076 1.148 2.59e-02 0.1006    
31  0.04376 -0.05733 -0.02782 -0.09871 1.354 3.39e-03 0.1803   *

Por ejemplo, para el modelo cherry.m1 ajustado a los datos de árboles de cerezo:

im <- influence.measures(cherry.m1)
head(round(im$infmat, 3))

  dfb.1_ dfb.l(G) dfb.l(H)  dffit cov.r cook.d   hat
1  0.015   -0.083    0.005  0.107 1.305  0.004 0.151
2  0.120   -0.082   -0.090  0.197 1.311  0.014 0.167
3  0.065   -0.021   -0.054  0.087 1.385  0.003 0.198
4 -0.011    0.021    0.004 -0.041 1.181  0.001 0.059
5  0.145    0.171   -0.170 -0.228 1.218  0.018 0.121
6  0.186    0.191   -0.212 -0.261 1.261  0.023 0.152

colSums(im$is.inf)

  dfb.1_ dfb.l(G) dfb.l(H)    dffit    cov.r   cook.d      hat 
       0        0        0        0        3        0        0 

Sólo la razón de covarianza identifica tres observaciones como “influyentes”. La observación con mayor distancia de Cook (número 18) tampoco altera sustancialmente los coeficientes al omitirse:

infl <- which.max(cooks.distance(cherry.m1))
cherry.infl <- update(cherry.m1, subset = -infl)
coef(cherry.m1)

(Intercept)  log(Girth) log(Height) 
  -6.691109    1.980412    1.132878 

coef(cherry.infl)

(Intercept)  log(Girth) log(Height) 
  -7.209148    1.957366    1.267528 

En cambio, al omitir una observación claramente no influyente, los coeficientes permanecen prácticamente iguales, confirmando que ninguna observación afecta de forma crítica al ajuste.

7.7 Corrigiendo problemas identificados

Al detectar debilidades en un GLM (secciones anteriores), puede seguirse esta estrategia:

1. Dependencia: si los \(y_i\) no son independientes, emplear métodos como generalized estimating equations, GLMM o GLMs espaciales.
   
2. Componente aleatorio: elegir el EDM según el tipo de datos—binomial para proporciones, Poisson o negativa binomial para conteos, gamma o inversa Gaussian para continuos positivos, Tweedie si hay ceros exactos. Si ningún EDM encaja, considerar cuasi-verosimilitud o modelos alternativos.
   
3. Componente sistemático: revisar el link (solo cambiarlo si conserva interpretabilidad), añadir variables omitidas o transformar covariables usando polinomios (poly()), splines (bs(), ns()) o términos basados en teoría previa.
   
4. Atípicos e influyentes: cuando se identifiquen, valorar modelos robustos, transformaciones específicas o, en casos justificados, la omisión cuidadosa de observaciones.

Ejemplo Diagnóstico y corrección en datos de cerezos

Como se vio en la Sect. 8.3, el modelo teórico

cherry.m1 <- glm(Volume ~ log(Girth) + log(Height),
                 family=Gamma(link="log"), data=trees)

es adecuado. A modo de ilustración, primero ajustamos un GLM gamma “ingenuo” con link recíproco y examinamos sus gráficos diagnósticos:

m.naive <- glm(Volume ~ Girth + Height, family=Gamma, data=trees)

# Residuos deviance estandarizados vs. log(Fitted)
scatter.smooth(rstandard(m.naive) ~ log(fitted(m.naive)), las=1,
               xlab="log(Fitted values)", ylab="Standardized residuals")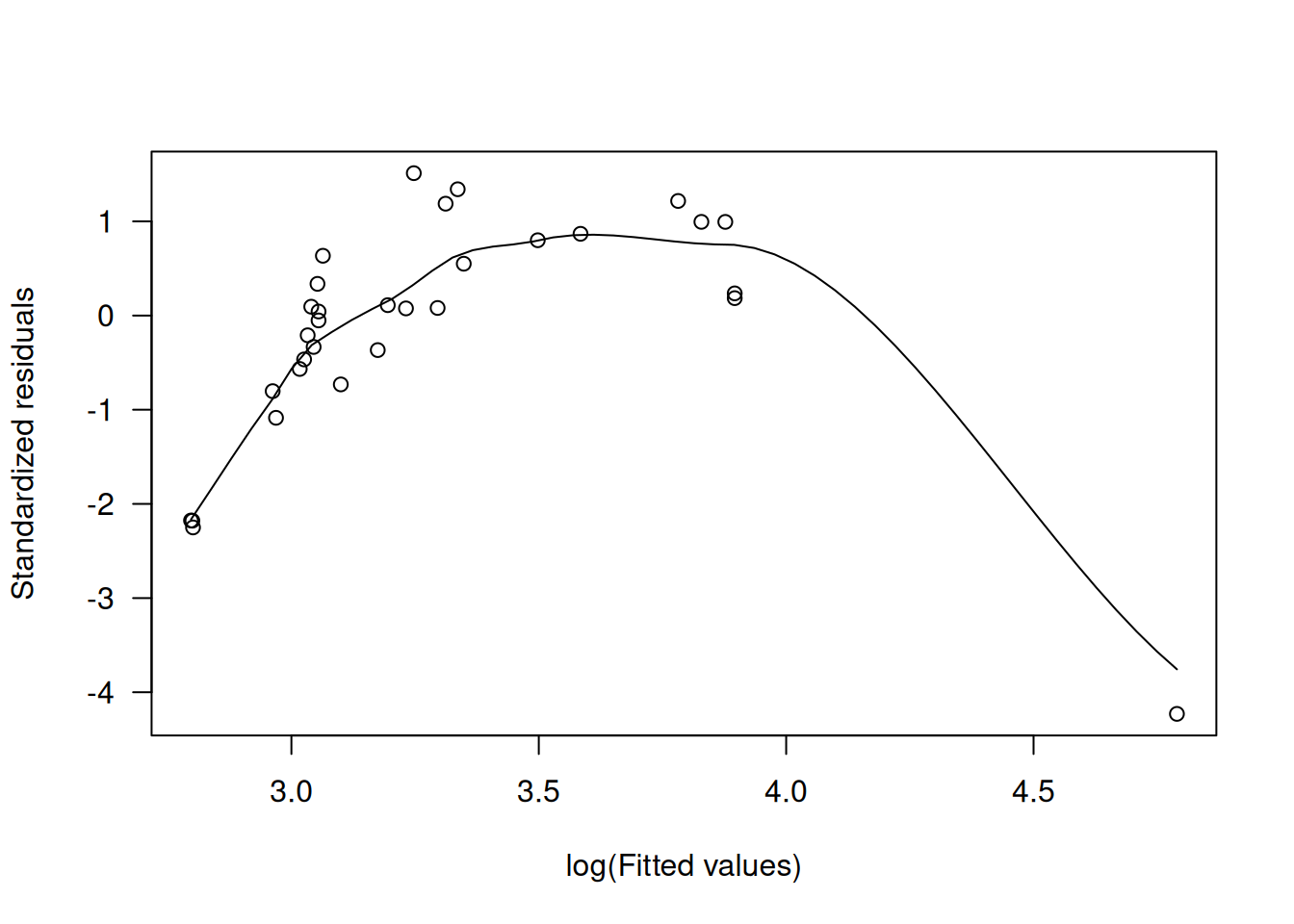

# Residuos vs. Girth y Height
scatter.smooth(rstandard(m.naive) ~ trees$Girth, las=1,
               xlab="Girth", ylab="Standardized residuals")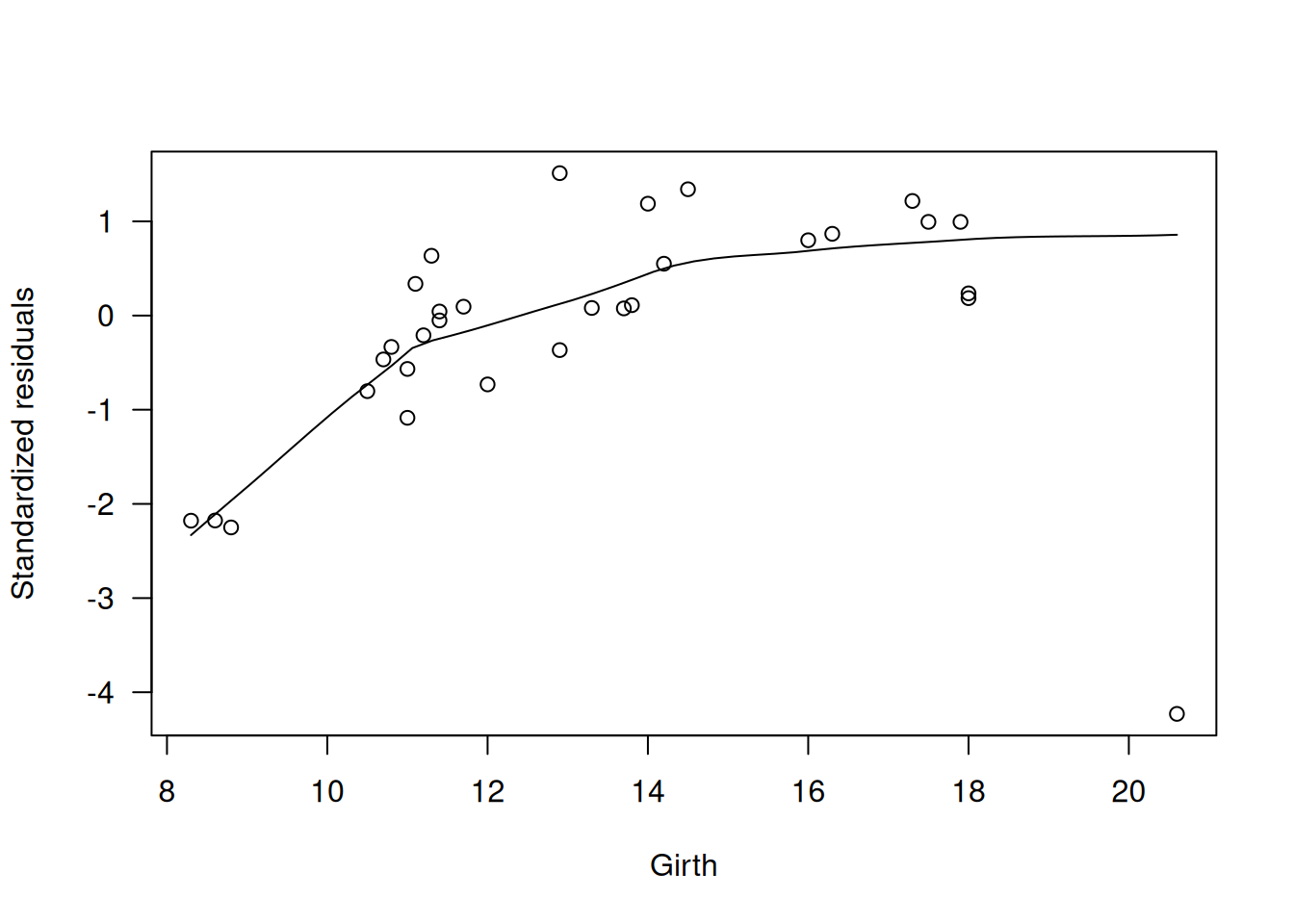

scatter.smooth(rstandard(m.naive) ~ trees$Height, las=1,
               xlab="Height", ylab="Standardized residuals")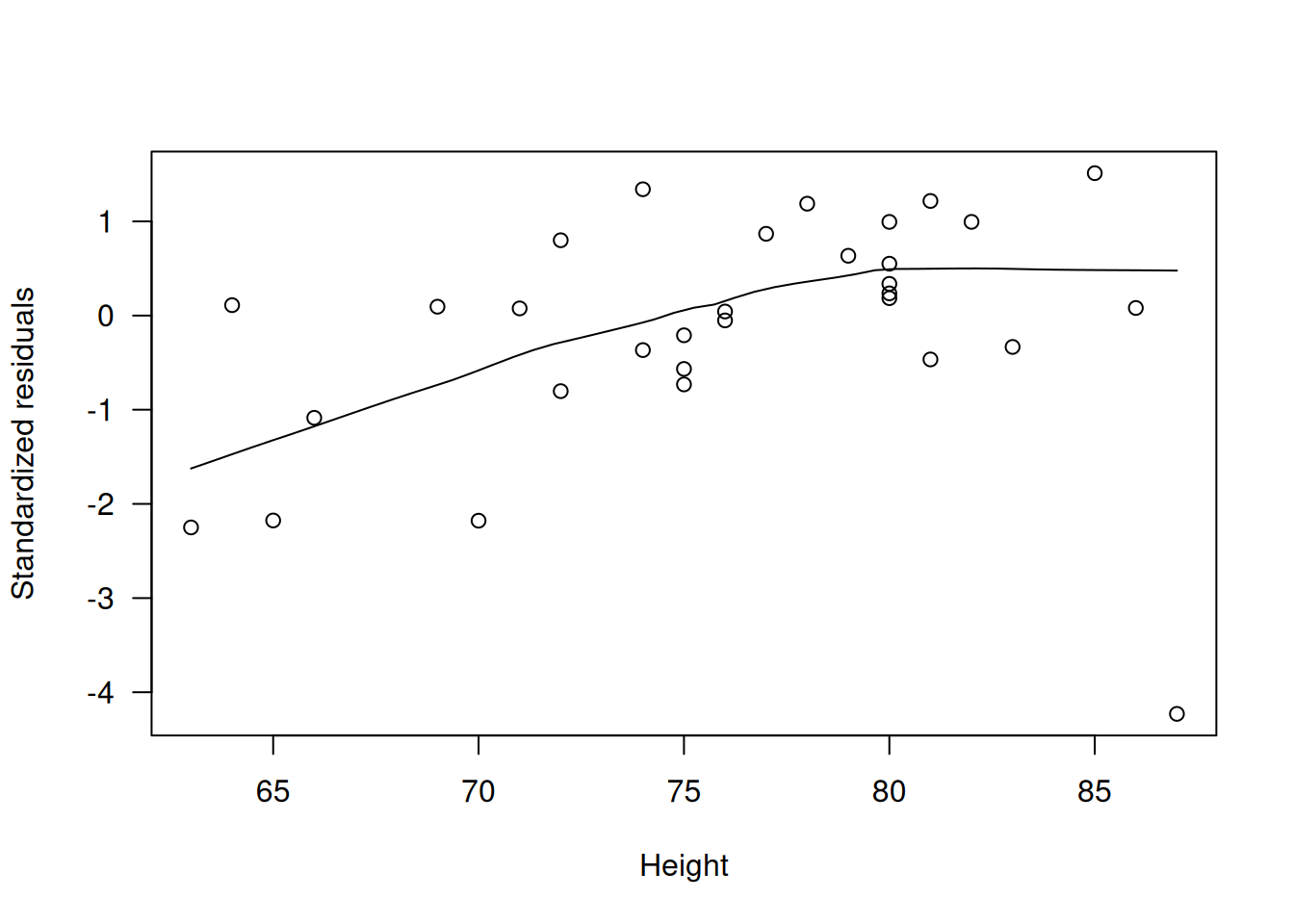

# Respuestas de trabajo z vs. predictor lineal η
eta  <- m.naive$linear.predictor
z    <- resid(m.naive, type="working") + eta
plot(z ~ eta, las=1,
     xlab="Linear predictor, η", ylab="Working responses, z")
abline(0, 1, col="grey")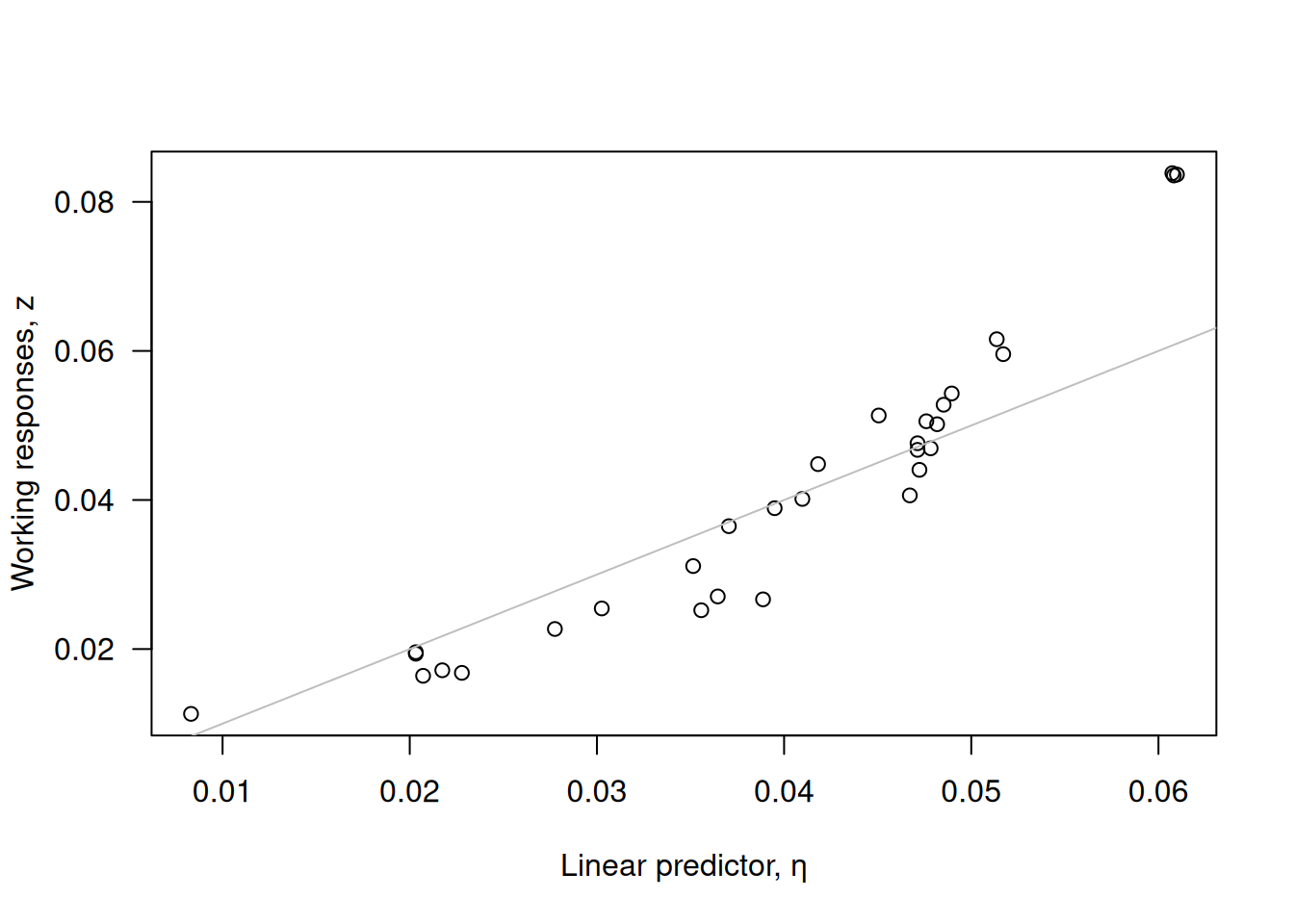

# Gráficos parciales
termplot(m.naive, partial.resid=TRUE, las=1)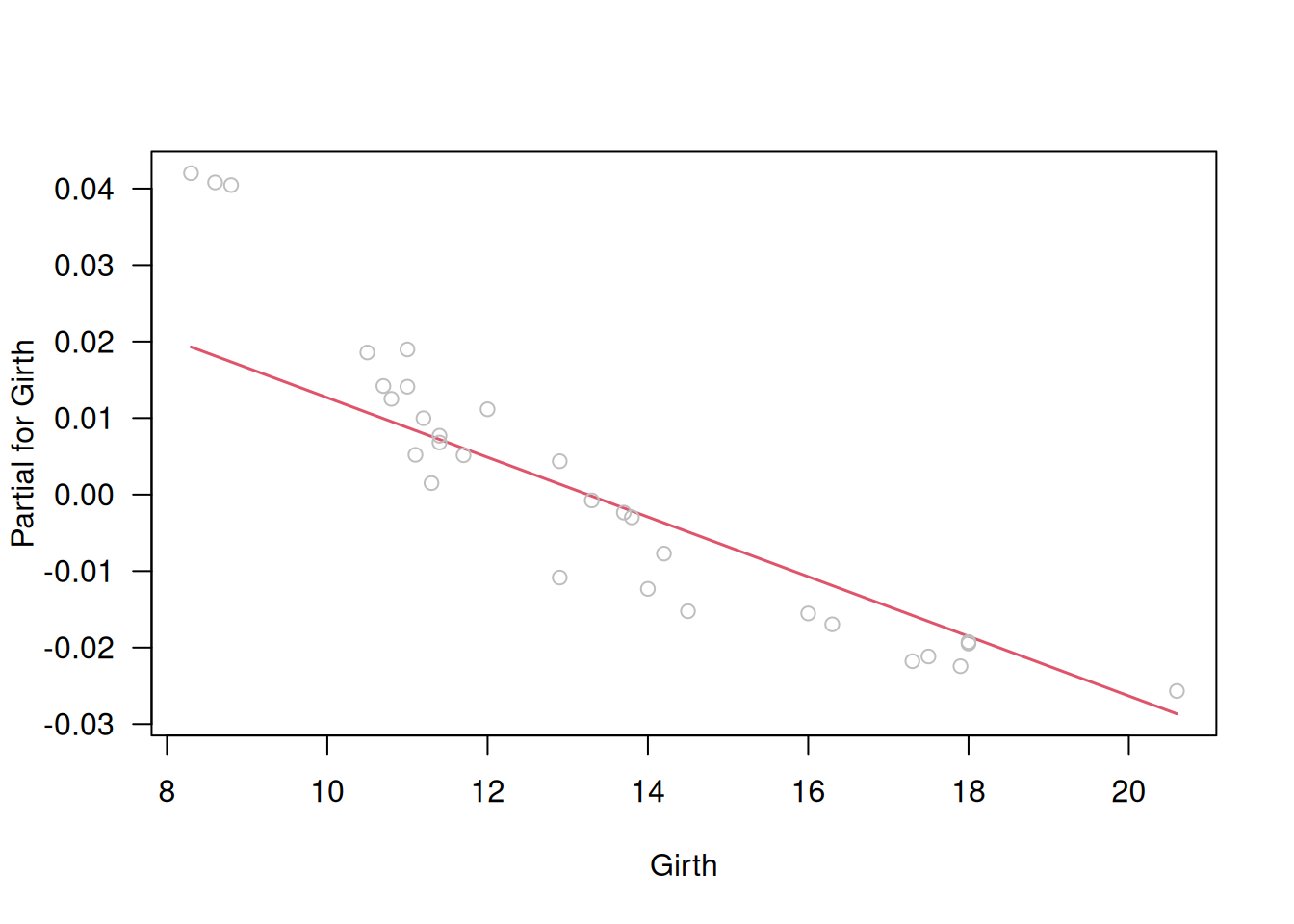

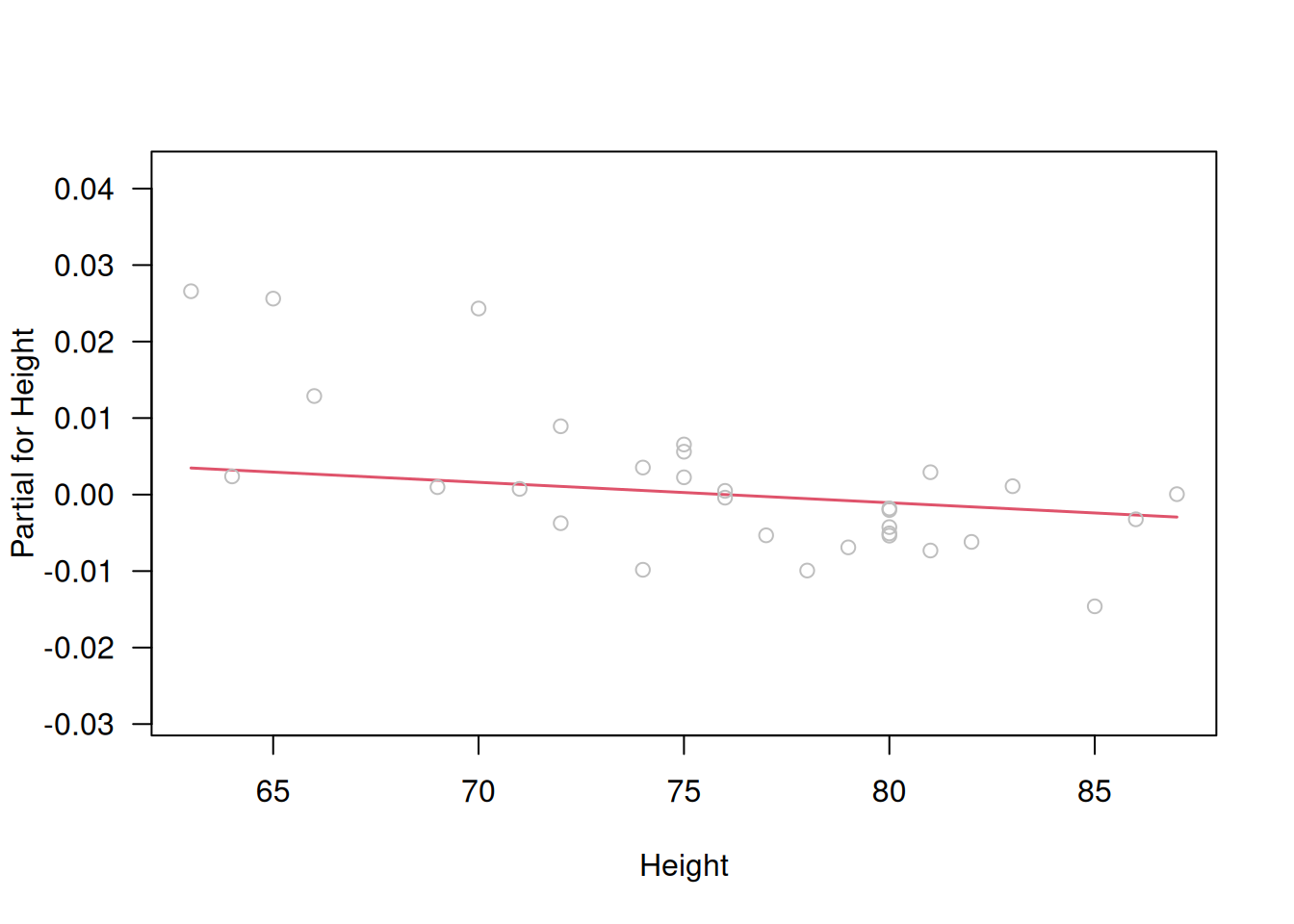
Estos gráficos muestran claras tendencias en \(r_D'\), incumplimiento de la línea \(z=\eta\) y curvas en los parciales, indicando enlace y transformaciones inapropiados.

A continuación, cambiamos al link logarítmico:

m.better <- update(m.naive, family=Gamma(link="log"))

# Misma serie de gráficos para m.better
scatter.smooth(rstandard(m.better) ~ log(fitted(m.better)), las=1,
               xlab="log(Fitted values)", ylab="Standardized residuals")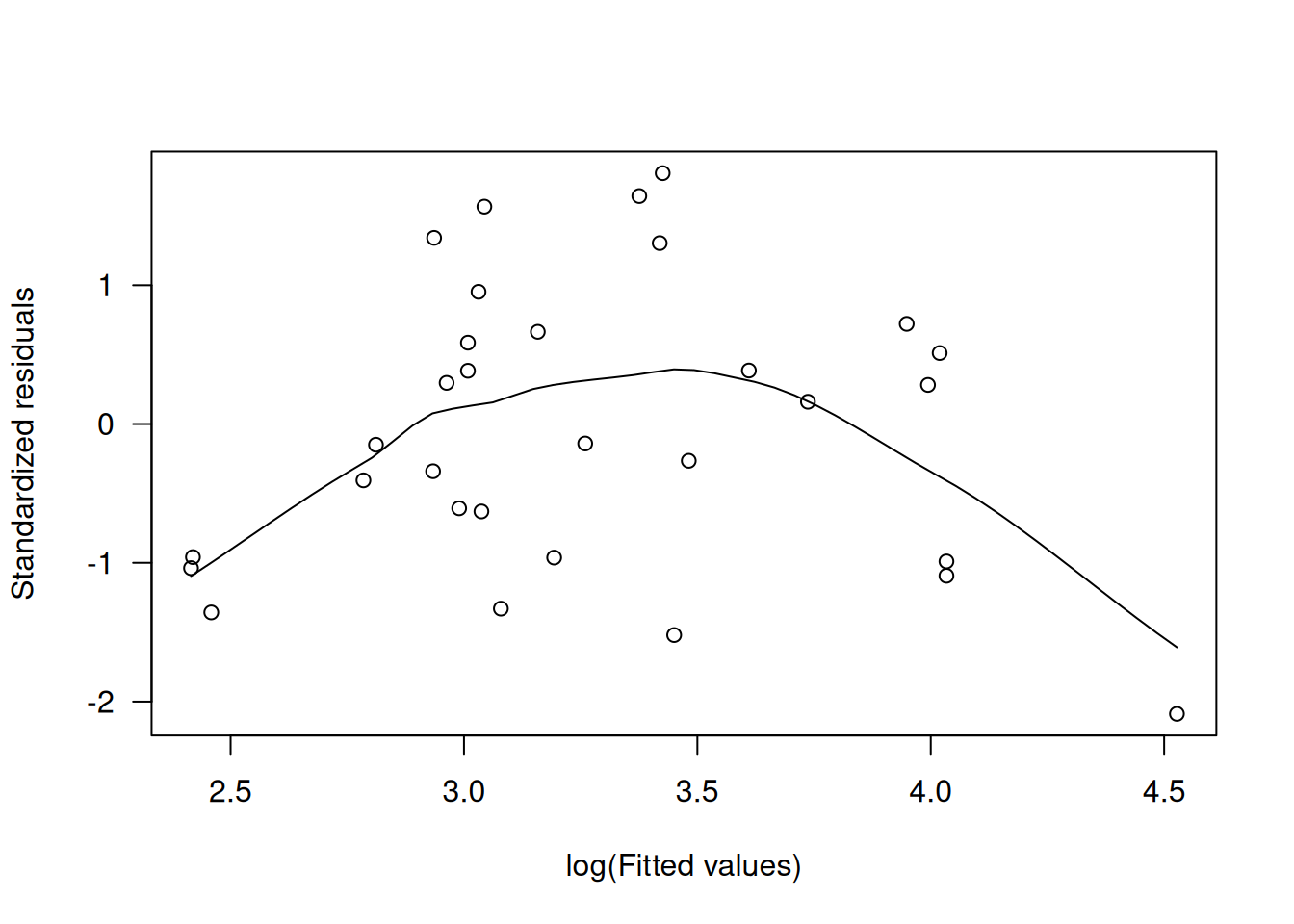

scatter.smooth(rstandard(m.better) ~ trees$Girth, las=1,
               xlab="Girth", ylab="Standardized residuals")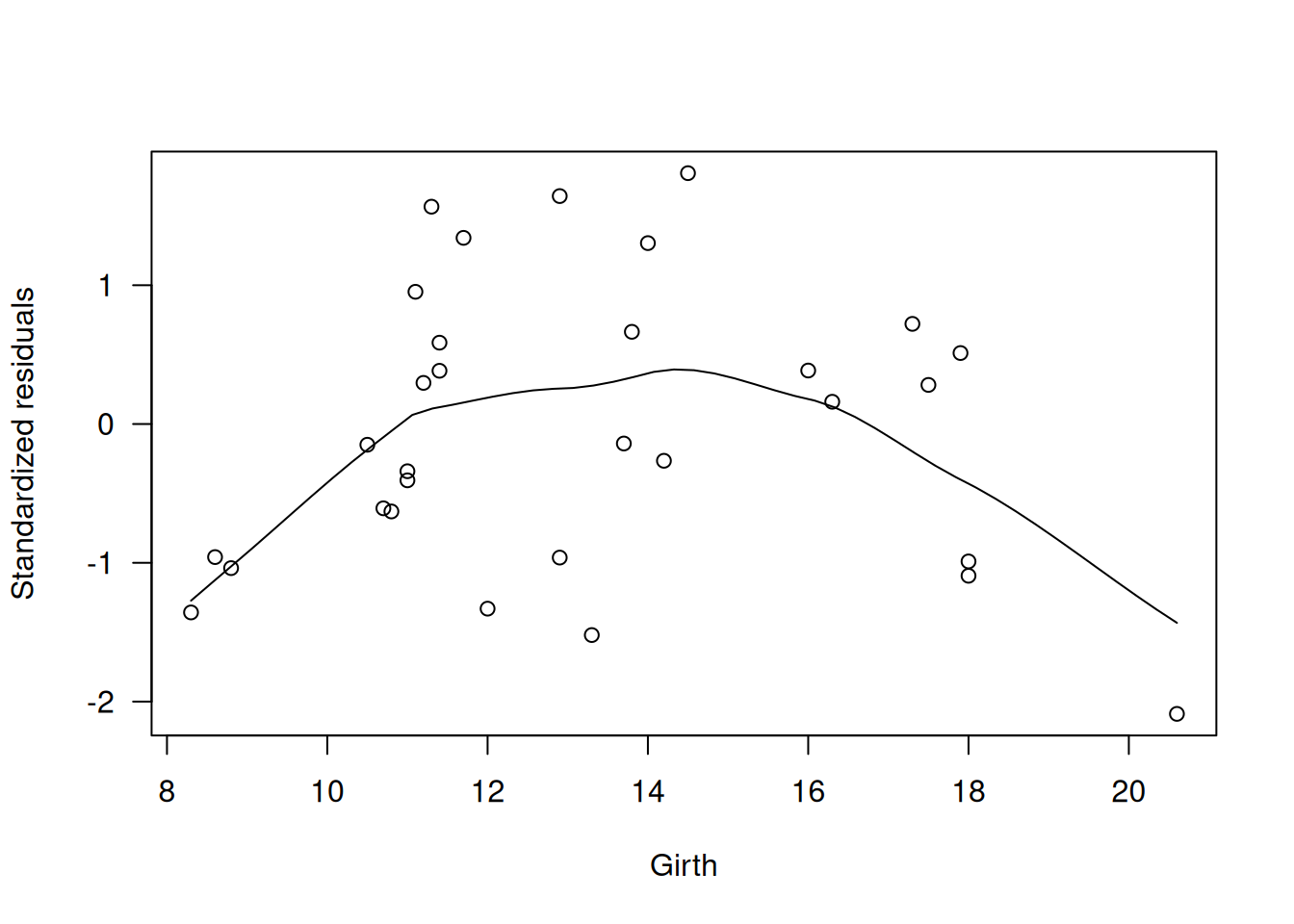

scatter.smooth(rstandard(m.better) ~ trees$Height, las=1,
               xlab="Height", ylab="Standardized residuals")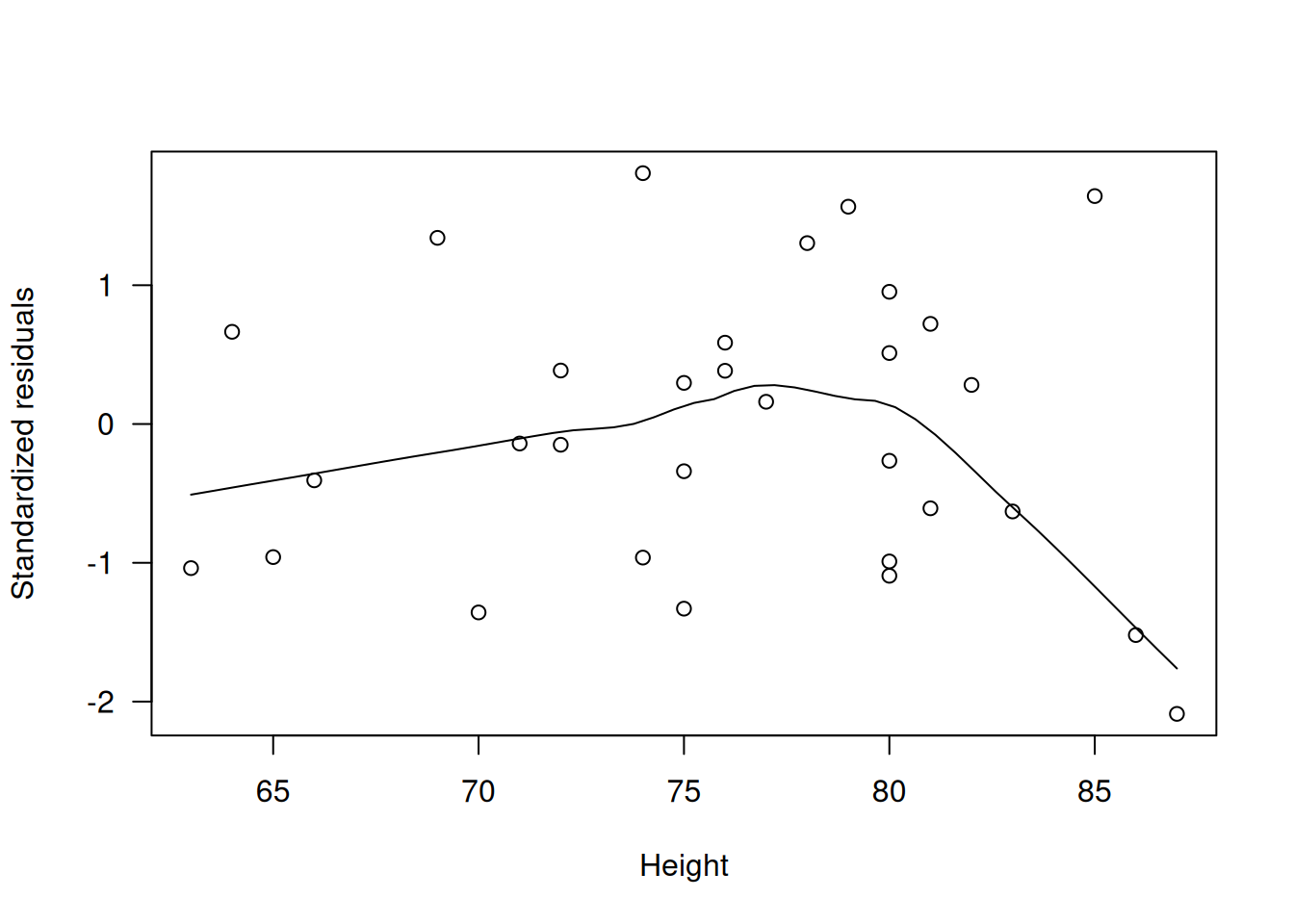

eta2 <- m.better$linear.predictor
z2   <- resid(m.better, type="working") + eta2
plot(z2 ~ eta2, las=1,
     xlab="Linear predictor, η", ylab="Working responses, z")
abline(0, 1, col="grey")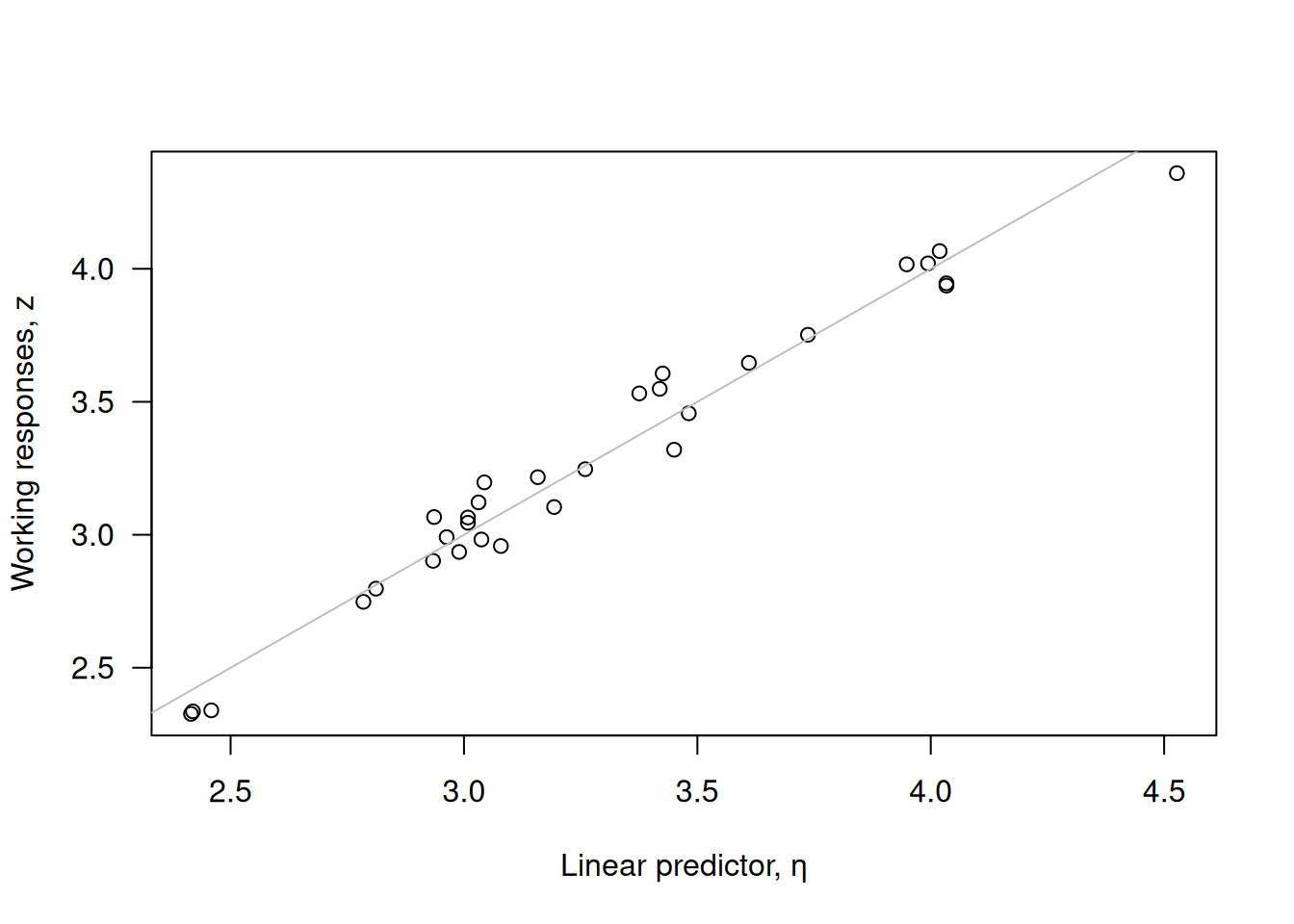

termplot(m.better, partial.resid=TRUE, las=1)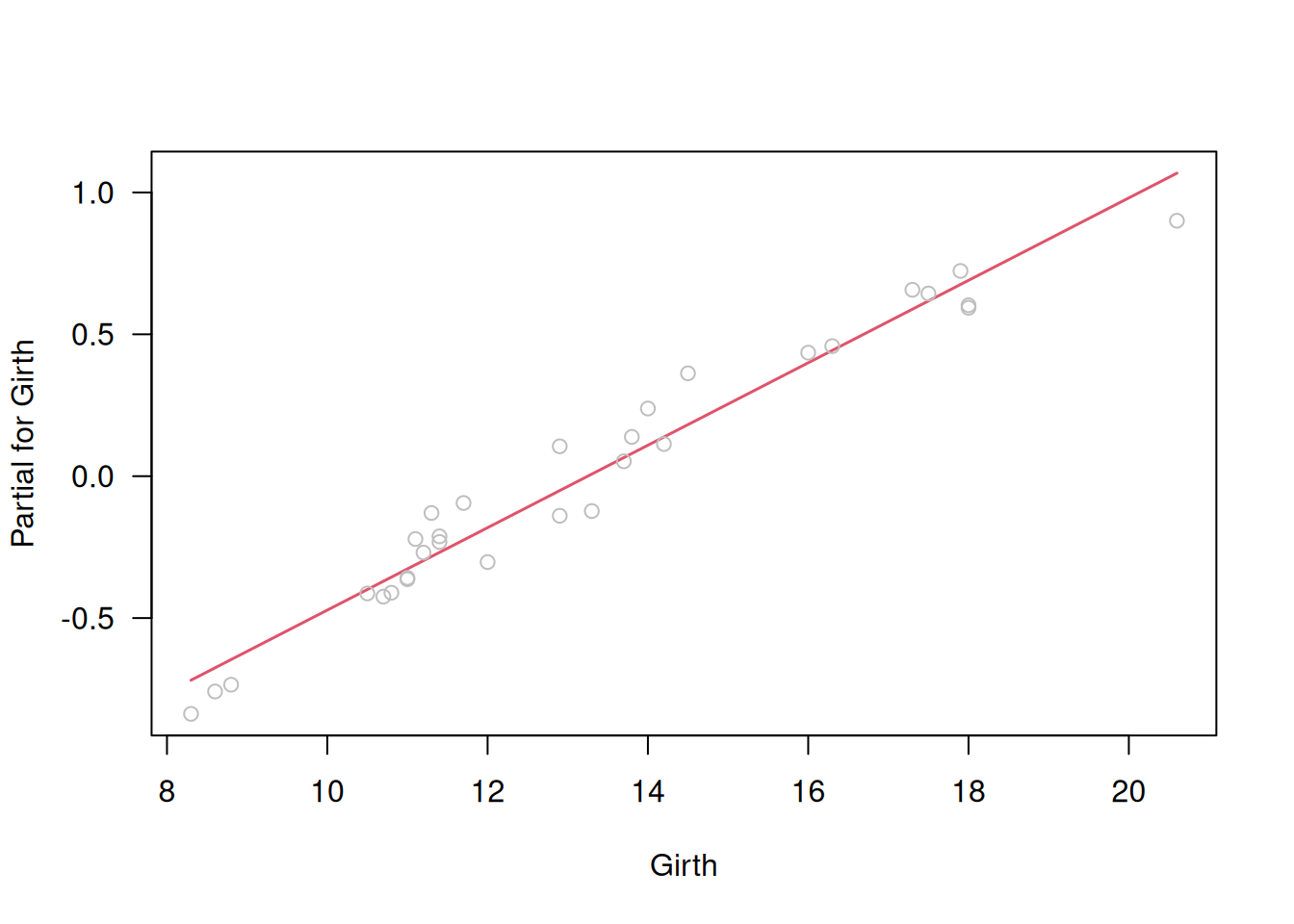

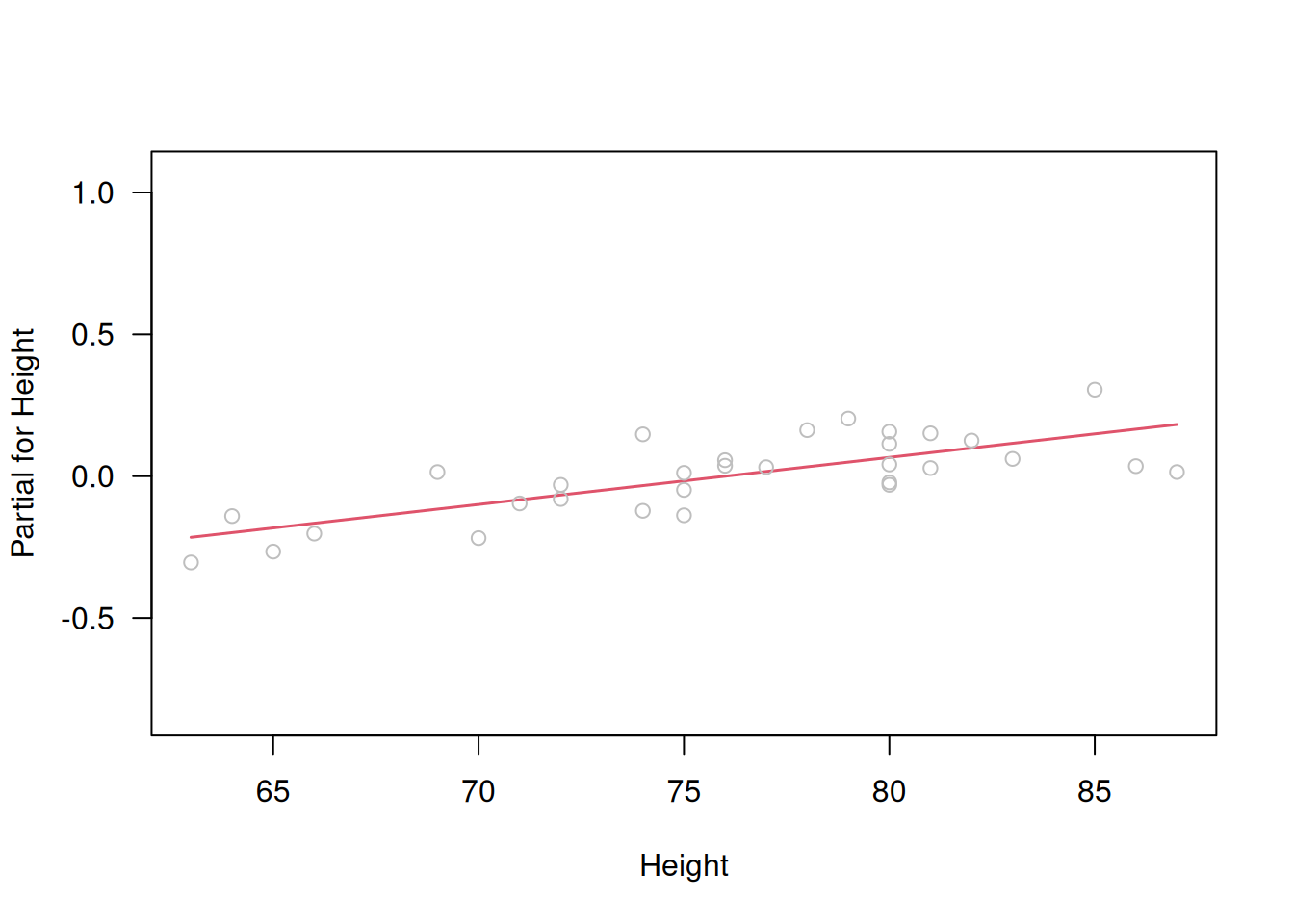
Con el link log, mejoran los gráficos de \(z\) vs. \(\eta\) y los parciales, aunque aún persisten ligeras tendencias en \(r_D'\).

7.8 Cuasi-verosimilitud y cuasi-verosimilitud extendida

En ocasiones la relación media-varianza sugerida por los datos no coincide con ningún miembro de la familia EDM, lo que impide definir una verosimilitud tradicional. Sin embargo, para cualquier EDM es válida la derivada

\[ \frac{\partial \log \mathcal{P}(\mu, \phi ; y)}{\partial \mu}=\frac{y-\mu}{\phi V(\mu)} \]

que es la base del ajuste de GLMs. Motivados por esto, definimos una “cuasi-probabilidad” cuya derivada respete la misma forma cuando solo conocemos la función de varianza (V()):

\[ \frac{\partial \log \overline{\mathcal{P}}(y ; \mu, \phi)}{\partial \mu}=\frac{y-\mu}{\phi V(\mu)}\,. \tag{8.7} \]

Al integrar en \(\mu\) obtenemos la cuasi-log-verosimilitud

\[ \mathcal{Q}(y;\mu)=\sum_{i=1}^{n}\int^{\mu_i}\frac{y_i-u}{\phi V(u)/w_i}\,du\,, \]

que se comporta como un log-likelihood para estimar \(\beta\) y sus errores, pero sin corresponder a ninguna distribución real. En este contexto no existen AIC ni residuales basados en CDF.

La devianza unitaria se deriva de forma análoga y depende únicamente de \(V(\mu)\):

\[ d(y,\mu)=2\int_{\mu}^{y}\frac{y-u}{V(u)}\,du\,, \tag{8.8} \]

y la devianza total es su suma ponderada habitual. Cuando \(V(\mu)\) proviene de un EDM, estas fórmulas coinciden con las de máxima verosimilitud.

La cuasi-verosimilitud garantiza que la estimación de GLMs sea consistente siempre que se cumplan los supuestos sobre media y varianza, incluso si la distribución está mal especificada. Los modelos más habituales son los quasi-Poisson (para sobredispersión en conteos) y quasi-binomial (para sobredispersión en proporciones), que en R se ajustan con family=quasipoisson() y family=quasibinomial(). También existe la familia genérica family=quasi() para otros casos.

Para dotar de una forma completa a la cuasi-verosimilitud, la aproximación por saddlepoint introduce el término de normalización

\[ \log \tilde{\mathcal{P}}(y;\mu,\phi)=-\tfrac12\log\{2\pi\,\phi\,V(y)\}-\frac{d(y,\mu)}{2\phi}\,, \]

definiendo la cuasi-verosimilitud extendida cuya derivada en \(\phi\) recupera el estimador de devianza para \(\phi\). Esta extensión resulta esencial para modelar funciones de varianza con parámetros desconocidos o estructuras de dispersión dependientes de covariables.