9 Modelos de Conteo

9.1 Resumen de los GLMs de Poisson

El GLM de Poisson es la elección más habitual para modelar conteos, asumiendo que cada observación \(y_i\) sigue

\[ \mathcal{P}(y_i;\mu_i)=\frac{e^{-\mu_i}\,\mu_i^{y_i}}{y_i!},\quad y_i=0,1,2,\ldots,\;\mu_i>0. \]

Esta distribución pertenece a la familia exponencial de dispersión (EDM) con función de varianza \(V(\mu)=\mu\) y parámetro de dispersión \(\phi=1\). La devianza unitaria queda

\[ d(y,\mu)=2\Bigl[y\log\frac{y}{\mu}-(y-\mu)\Bigr], \]

y la devianza residual se define como

\[ D(y,\hat\mu)=\sum_{i=1}^n w_i\,d(y_i,\hat\mu_i), \]

donde \(w_i\) son pesos previos. Bajo la aproximación de saddlepoint, si \(y_i\ge3\), entonces \(D(y,\hat\mu)\sim\chi^2_{n-p'}\), siendo \(p'\) el número de parámetros en el predictor lineal.

El enlace canónico es el logarítmico, que garantiza positividad de \(\mu\) y da una interpretación multiplicativa de los coeficientes. El modelo general es

\[ \begin{aligned} y_i &\sim \mathrm{Pois}(\mu_i),\\ \log\mu_i &= \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}, \end{aligned} \]

o equivalentemente

\[ \mu_i = \exp(\beta_0)\;\prod_{j=1}^p\exp(\beta_j)^{\,x_{ij}}. \]

Así, incrementar \(x_j\) en una unidad multiplica \(\mu\) por \(\exp(\beta_j)\); si \(\beta_j=0\), entonces \(\mu\) no depende de \(x_j\).

En ciertos casos se emplean enlaces alternativos como “identity” o “sqrt”, pero la forma GLM(Pois; link) se especifica en R con family=poisson(). Cuando todas las covariables son cualitativas, el modelo se conoce como log‐lineal de tablas de contingencia; con covariables numéricas, hablamos de regresión de Poisson.

Con intercepto y enlace logarítmico, la devianza residual simplifica a

\[ D(y,\hat\mu)=2\sum_{i=1}^n w_i\,y_i\log\frac{y_i}{\hat\mu_i}, \]

pues \(\sum_i w_i(y_i-\hat\mu_i)=0\). Para diagnóstico, se recomiendan los residuos cuantil (qresid()), que facilitan la evaluación de la adecuación del modelo aleatorio.

9.2 Modelado de tasas

Cuando cada conteo \(y_i\) proviene de una población de tamaño \(T_i\) muy grande, tiene más sentido trabajar con la tasa de eventos \(y_i/T_i\) que con el simple conteo. Por ejemplo, comparar el número de casos de una enfermedad entre ciudades exige ajustar por la población de cada ciudad para obtener una tasa “justa” (p. ej. casos por mil habitantes). Aunque teóricamente podríamos usar un GLM binomial con pesos \(T_i\), en la práctica un GLM de Poisson con un offset es más cómodo cuando las tasas son pequeñas (digamos < 1 %).

Para modelar estas tasas usamos

\[ y_i\sim\mathrm{Pois}(\mu_i),\qquad \log\mu_i=\log T_i+\beta_0+\sum_{j}\beta_j x_{ij}, \]

es decir, incluimos \(\log T_i\) como offset (coeficiente 1 fijo) y las demás covariables \(x_{ij}\) (factores o numéricas) en el predictor lineal. De este modo

\[ \mathrm{E}\bigl[y_i/T_i\bigr]=\mu_i/T_i, \]

y no es necesario estimar ningún parámetro asociado a \(T_i\).

9.2.1 Ejemplo: tasas de cáncer de pulmón en Dinamarca

El conjunto danishlc contiene, para cuatro ciudades y seis grupos de edad, los casos (\(\mathrm{Cases}\)) y la población (\(\mathrm{Pop}\)). Tras construir la tasa por mil habitantes:

library(GLMsData)
data("danishlc")
danishlc$Rate <- danishlc$Cases / danishlc$Pop * 1000
danishlc$Age  <- ordered(danishlc$Age, levels=c("40-54","55-59","60-64","65-69","70-74",">74"))

un gráfico de Rate frente a City y Age sugiere un incremento con la edad salvo en la última categoría:

danishlc$City <- abbreviate(danishlc$City, 1) # Abbreviate city names
matplot( xtabs( Rate ~ Age+City, data=danishlc), pch=1:4, lty=1:4,
            type="b", lwd=2, col="black", axes=FALSE, ylim=c(0, 25),
        xlab="Age group", ylab="Cases/1000")
axis(side=1, at=1:6, labels=levels(danishlc$Age))
axis(side=2, las=1); box()
legend("topleft", col="black", pch=1:4, lwd=2, lty=1:4, merge=FALSE,
    legend=c("Fredericia", "Horsens", "Kolding", "Vejle") )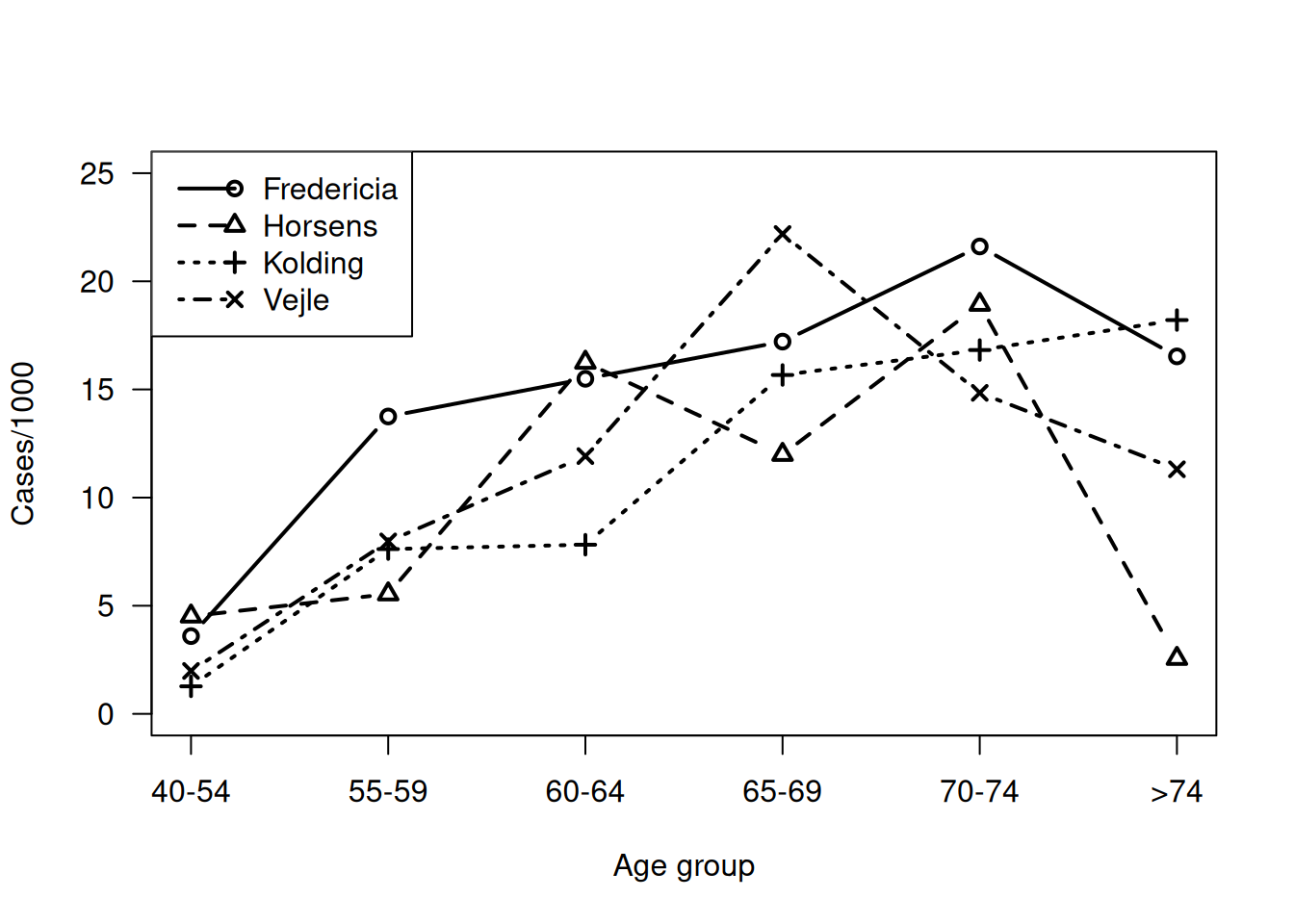

Al declarar una variable ordenada con ordered() en R, el sistema asigna por defecto contrastes polinomiales (contr.poly), que asumen distancias iguales entre niveles y resultan poco interpretables cuando las categorías no están equiespaciadas. Para forzar el uso de los contrastes de tratamiento habituales (donde cada nivel se compara con un nivel base), incluso en factores ordenados, debe redefinirse la opción global de contrastes:

options(contrasts = c("contr.treatment", "contr.treatment"))

El primer elemento ("contr.treatment") corresponde a factores no ordenados (valor por defecto).
El segundo elemento redefine los contrastes para factores ordenados, sustituyendo contr.poly por contr.treatment.

Para ajustar el GLM con interacción:

dlc.m1 <- glm(Cases ~ offset(log(Pop)) + City*Age,
              family=poisson, data=danishlc)
anova(dlc.m1, test="Chisq")

Analysis of Deviance Table

Model: poisson, link: log

Response: Cases

Terms added sequentially (first to last)

         Df Deviance Resid. Df Resid. Dev Pr(>Chi)    
NULL                        23    129.908             
City      3    3.393        20    126.515  0.33495    
Age       5  103.068        15     23.447  < 2e-16 ***
City:Age 15   23.447         0      0.000  0.07509 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Tanto la interacción como City no resultan significativos, así que simplificamos a un modelo solo en función de la edad:

dlc.m2 <- update(dlc.m1, . ~ offset(log(Pop)) + Age)

También cabe tratar Age como variable numérica (AgeNum) o incluso ajustarla con polinomios:

danishlc$AgeNum <- rep( c(40, 55, 60, 65, 70, 75), 4)
dlc.m3 <- update(dlc.m1, . ~ offset(log(Pop)) + AgeNum)
dlc.m4 <- update(dlc.m3, . ~ offset(log(Pop)) + poly(AgeNum, 2))
anova(dlc.m3, dlc.m4, test="Chisq")

Analysis of Deviance Table

Model 1: Cases ~ AgeNum + offset(log(Pop))
Model 2: Cases ~ poly(AgeNum, 2) + offset(log(Pop))
  Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
1        22     48.968                          
2        21     32.500  1   16.468 4.948e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La comparación por AIC

AIC(dlc.m1, dlc.m2, dlc.m3, dlc.m4)

       df      AIC
dlc.m1 24 144.3880
dlc.m2  6 136.6946
dlc.m3  2 149.3556
dlc.m4  3 134.8876

sugiere que el modelo cuadrático en edad (dlc.m4) ofrece el mejor compromiso de ajuste/predicción, aunque el modelo categórico simple (dlc.m2) apenas lo empeora y es más interpretable.

El uso de la aproximación saddlepoint para que la deviancia residual siga aproximadamente una \(\chi^2\) requiere que todos los recuentos cumplan \(y_i>3\). En el caso de los datos daneses de incidencia de cáncer de pulmón, al ordenar los recuentos observados comprobamos:

sort(danishlc$Cases)

 [1]  2  4  5  6  7  7  7  8  8  9 10 10 10 10 11 11 11 11 11 12 12 13 14 15

Solo una observación es 2, por lo que la condición se incumple levemente. Aun así, procedemos a la prueba de bondad de ajuste para dos modelos: uno con edad como factor (dlc.m2) y otro con un término cuadrático en la edad (dlc.m4). Calculamos la deviancia residual y el \(P\)-valor de la prueba chi-cuadrado:

D.m2 <- deviance(dlc.m2)
df.m2 <- df.residual(dlc.m2)
c( Dev=D.m2, df=df.m2,
   P = pchisq(D.m2, df.m2, lower.tail=FALSE) )

        Dev          df           P 
28.30652745 18.00000000  0.05754114

D.m4 <- deviance(dlc.m4)
df.m4 <- df.residual(dlc.m4)
c( Dev=D.m4, df=df.m4,
   P = pchisq(D.m4, df.m4, lower.tail=FALSE) )

        Dev          df           P 
32.49959158 21.00000000  0.05206888

Ambos \(P\)-valores (aprox. 0.058 y 0.052) son mayores que 0.05, indicando que ninguno de los dos modelos muestra falta de ajuste significativa al 5%.

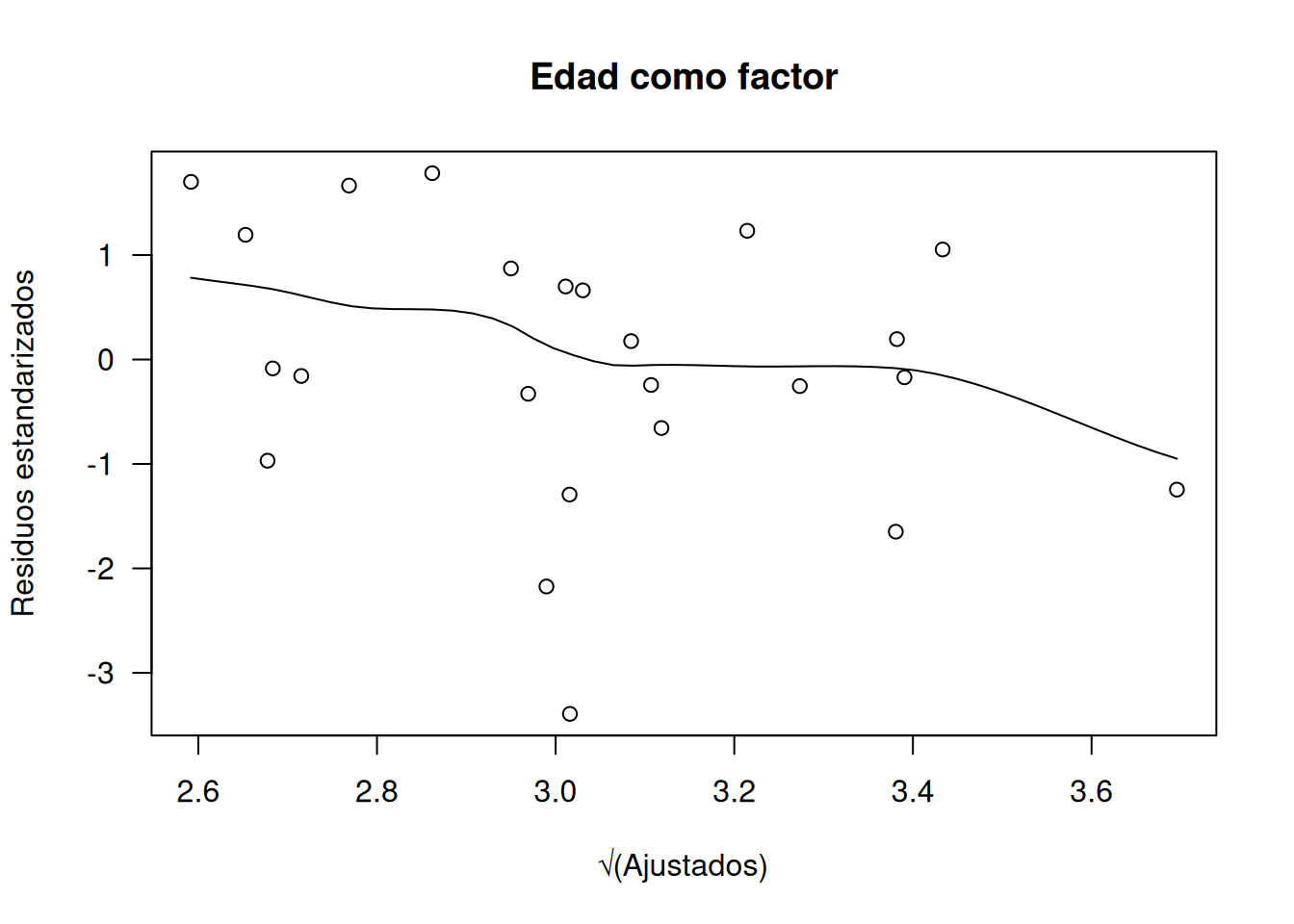
Para confirmar la adecuación, examinamos residuos estandarizados y otras gráficas de diagnóstico usando residuos cuántiles (función qresid() del paquete statmod):

library(statmod)

# Modelo con edad como factor (dlc.m2)
scatter.smooth(
  rstandard(dlc.m2) ~ sqrt(fitted(dlc.m2)),
  ylab="Residuos estandarizados", xlab="√(Ajustados)",
  main="Edad como factor", las=1
)

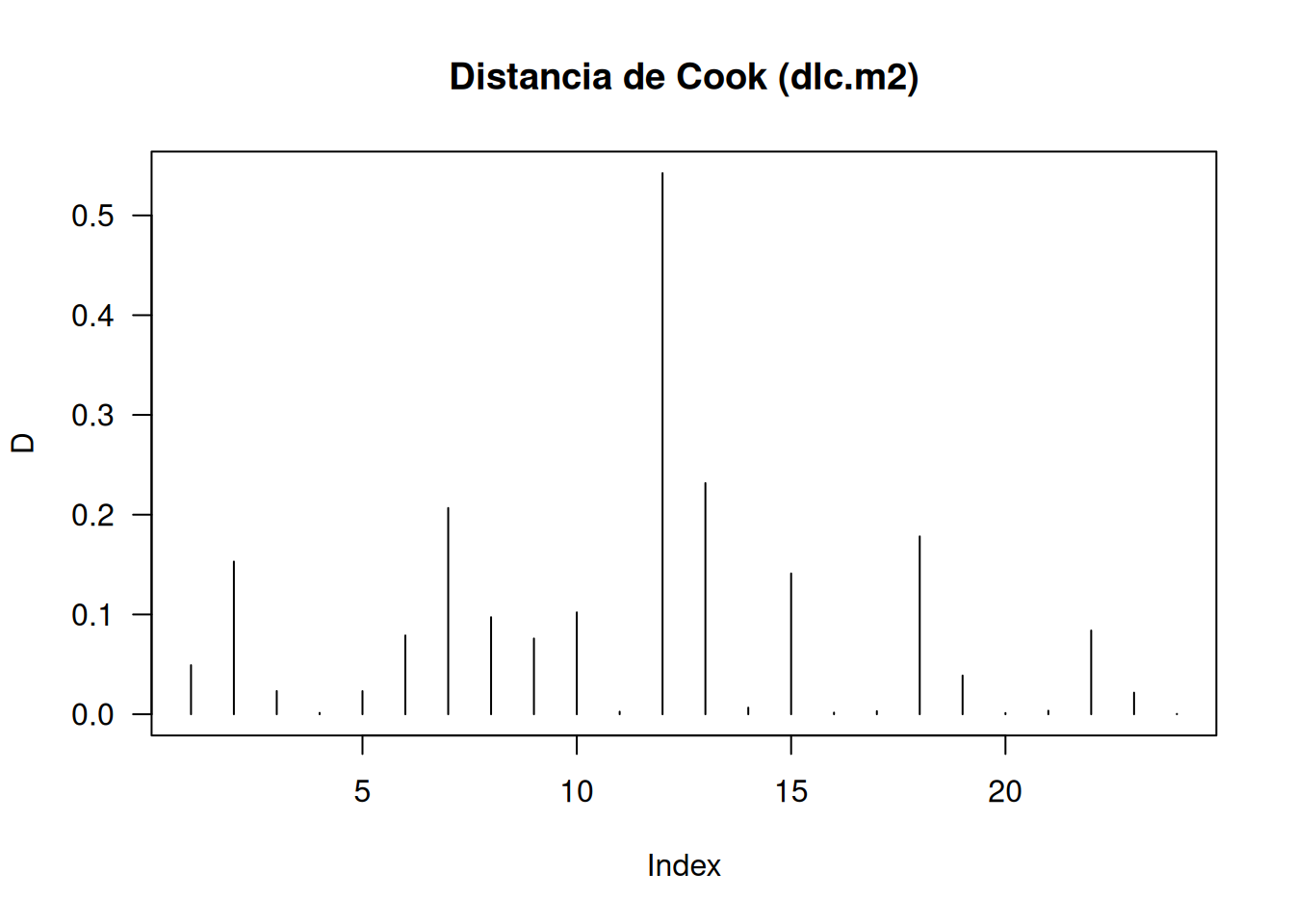
plot(
  cooks.distance(dlc.m2), type="h", las=1,
  main="Distancia de Cook (dlc.m2)", ylab="D"
)

qqnorm(qresid(dlc.m2), las=1); abline(0,1)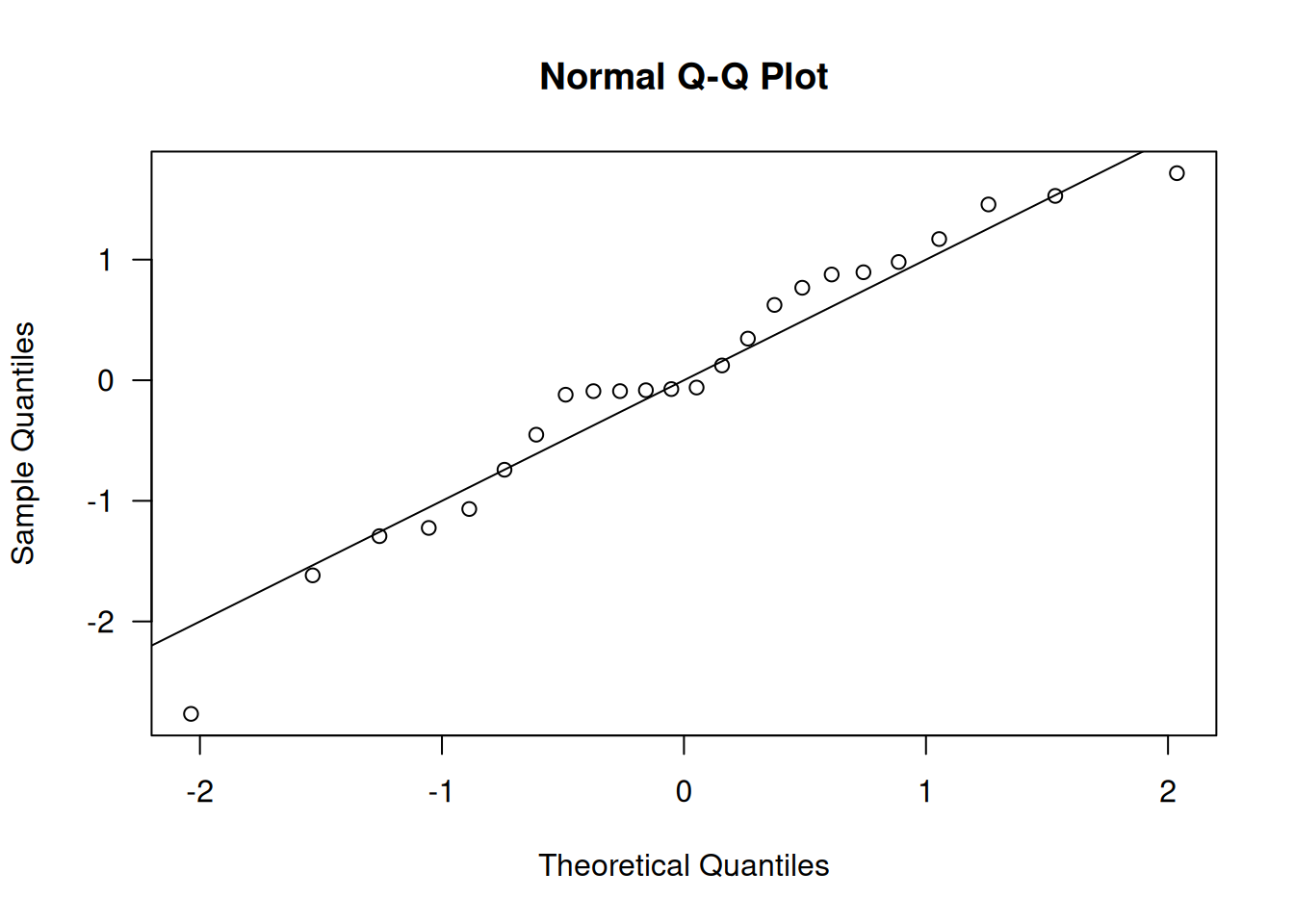

# Modelo con edad cuadrática (dlc.m4)
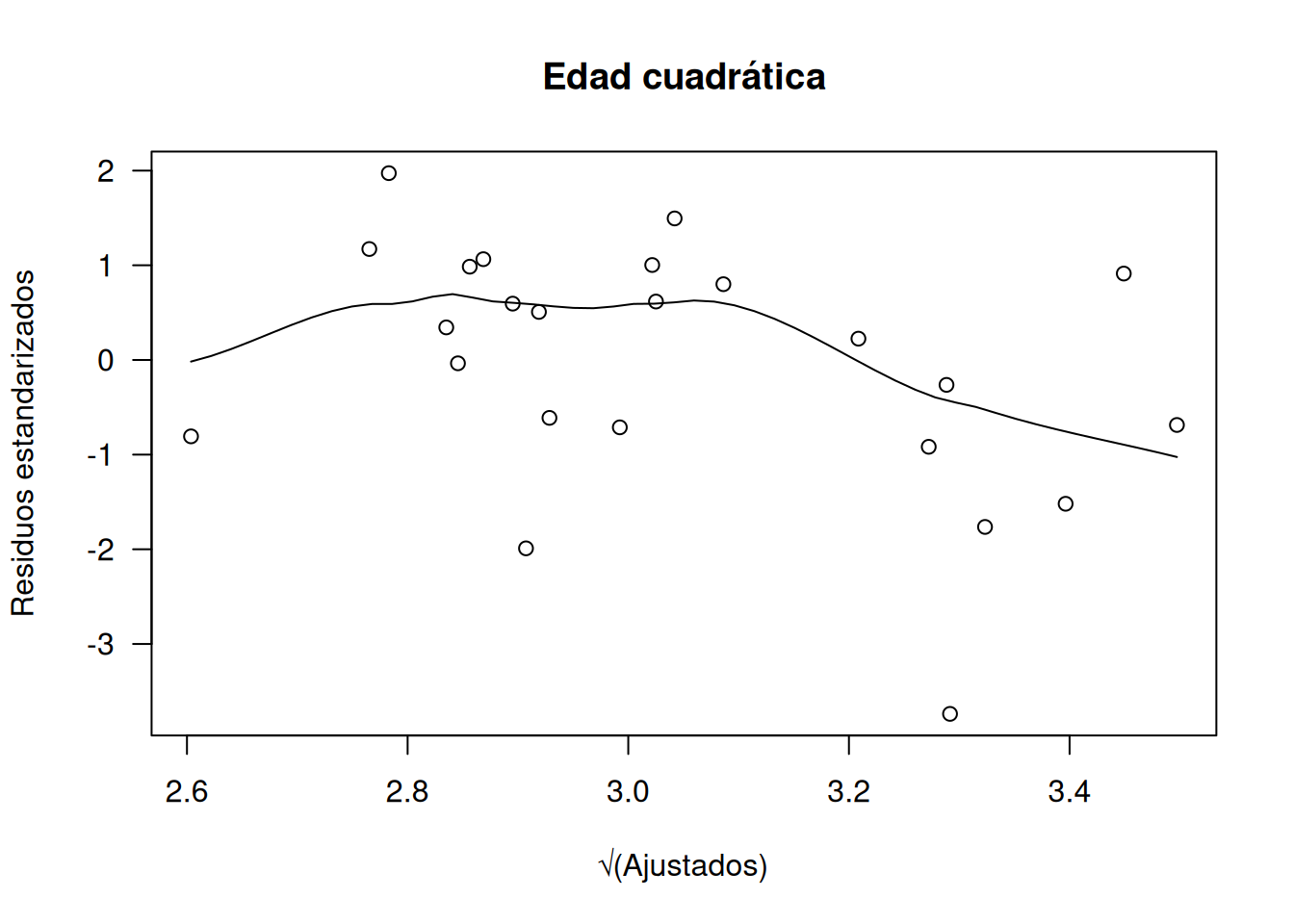
scatter.smooth(
  rstandard(dlc.m4) ~ sqrt(fitted(dlc.m4)),
  ylab="Residuos estandarizados", xlab="√(Ajustados)",
  main="Edad cuadrática", las=1
)

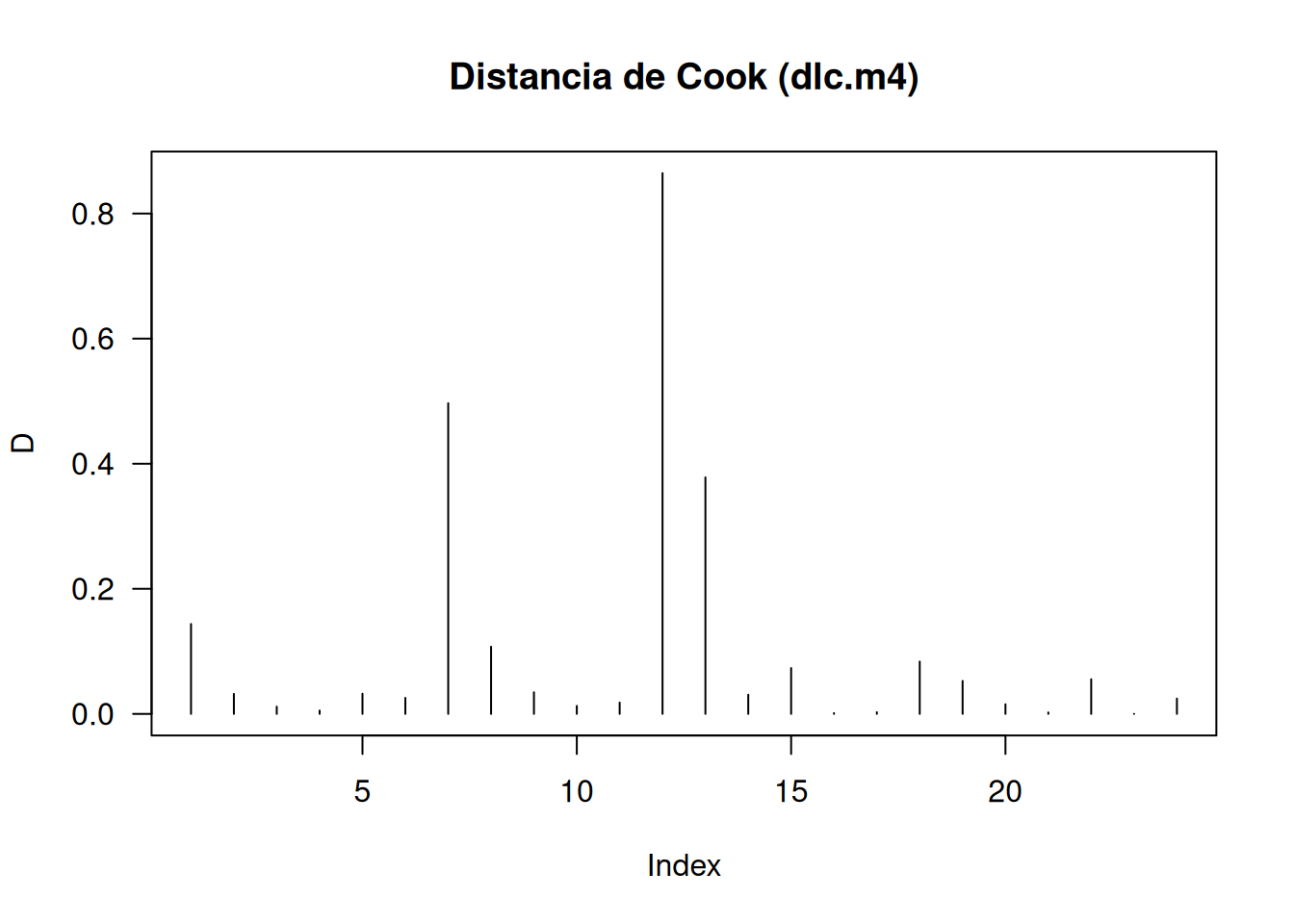
plot(
  cooks.distance(dlc.m4), type="h", las=1,
  main="Distancia de Cook (dlc.m4)", ylab="D"
)

qqnorm(qresid(dlc.m4), las=1); abline(0,1)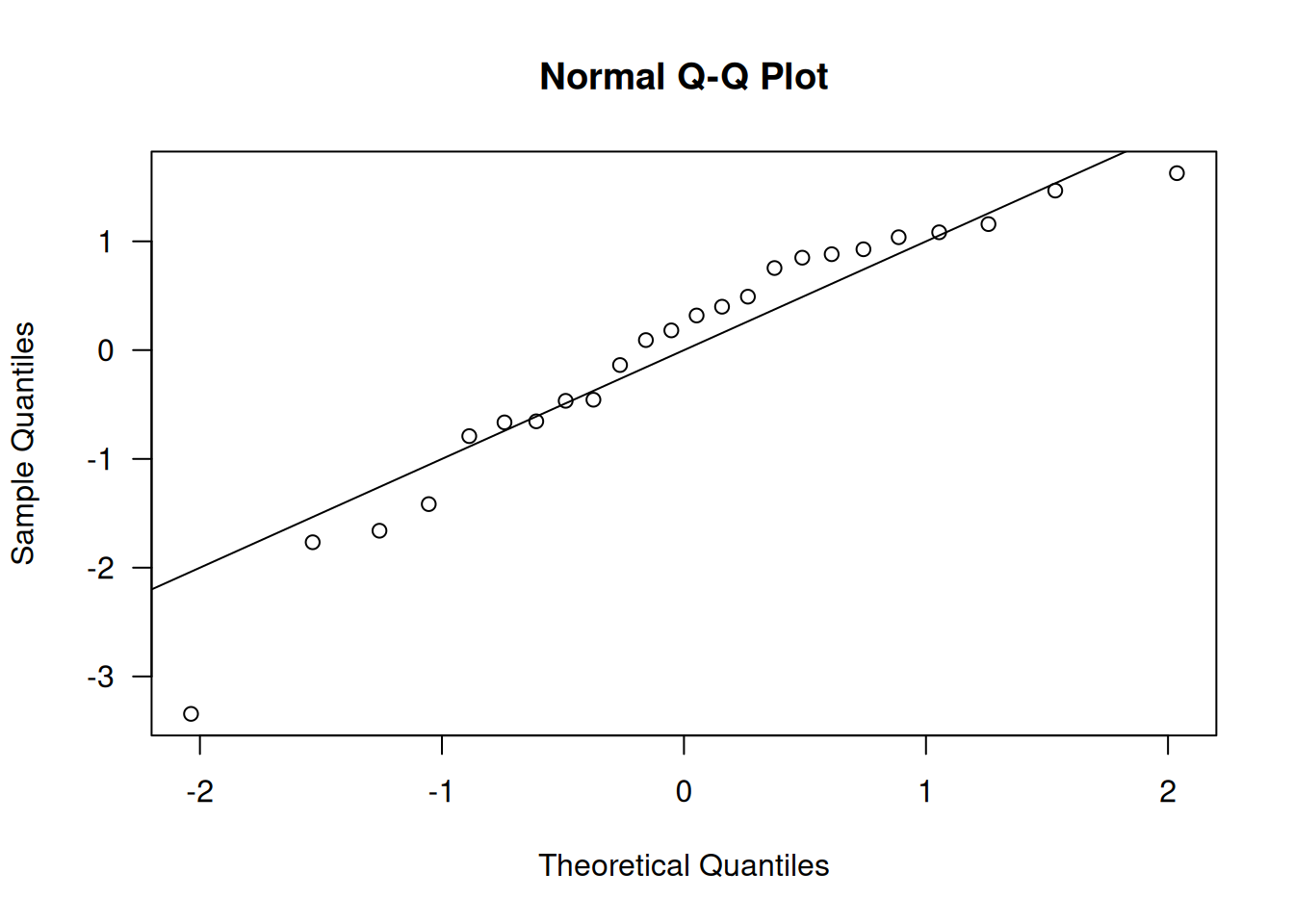

Las gráficas muestran varianza aproximadamente constante en los residuos estandarizados, distancias de Cook sin puntos excesivamente influyentes en dlc.m2 y solo unos pocos en dlc.m4, y Q–Q plots bastante lineales. En conjunto, ambos modelos resultan razonablemente adecuados, aunque se prefiere dlc.m2 por su simplicidad y menor número de observaciones influyentes.

9.3 Sobredispersión

9.3.1 Sobredispersión para GLMs de Poisson

En la distribución Poisson clásica se cumple \(\operatorname{var}[y]=\mu\), pero en la práctica con frecuencia la varianza observada excede a la media. Este fenómeno, llamado sobredispersión, puede deberse a que la verdadera media \(\mu\) varíe entre réplicas aun con los mismos explicativos, o a que los eventos ocurran en clusters, introduciendo correlación positiva entre observaciones. Aunque las estimaciones \(\hat\beta_j\) sigan siendo consistentes, los errores estándar quedan subestimados, de modo que los contrastes resultan excesivamente optimistas y los intervalos de confianza demasiado estrechos.

La detección de sobredispersión se efectúa mediante pruebas de bondad de ajuste: si la deviancia residual o el estadístico de Pearson superan con creces los grados de libertad residuales y persiste la falta de ajuste tras haber incluido todos los explicativos y eliminado posibles atípicos, la explicación más plausible es la sobredispersión. Cuando los conteos son muy pequeños y las aproximaciones asintóticas dudosas (Sect. 7.5),estadísticos de bondad de ajuste altos siguen siendo indicativos de falta de ajuste.

9.3.1.1 Ejemplo: Sobredispersión en datos de “pock marks”

En un experimento de actividad vírica se contaron pústulas a varias diluciones del medio (datos en pock). Usamos como covariable \(\log_{2}(\mathtt{Dilution})\) y examinamos la relación media–varianza por grupo:

data(pock)
plot( Count ~ jitter(log2(Dilution)), data=pock, las=1,
    xlab="Log (base 2) of dilution", ylab="Pock mark count")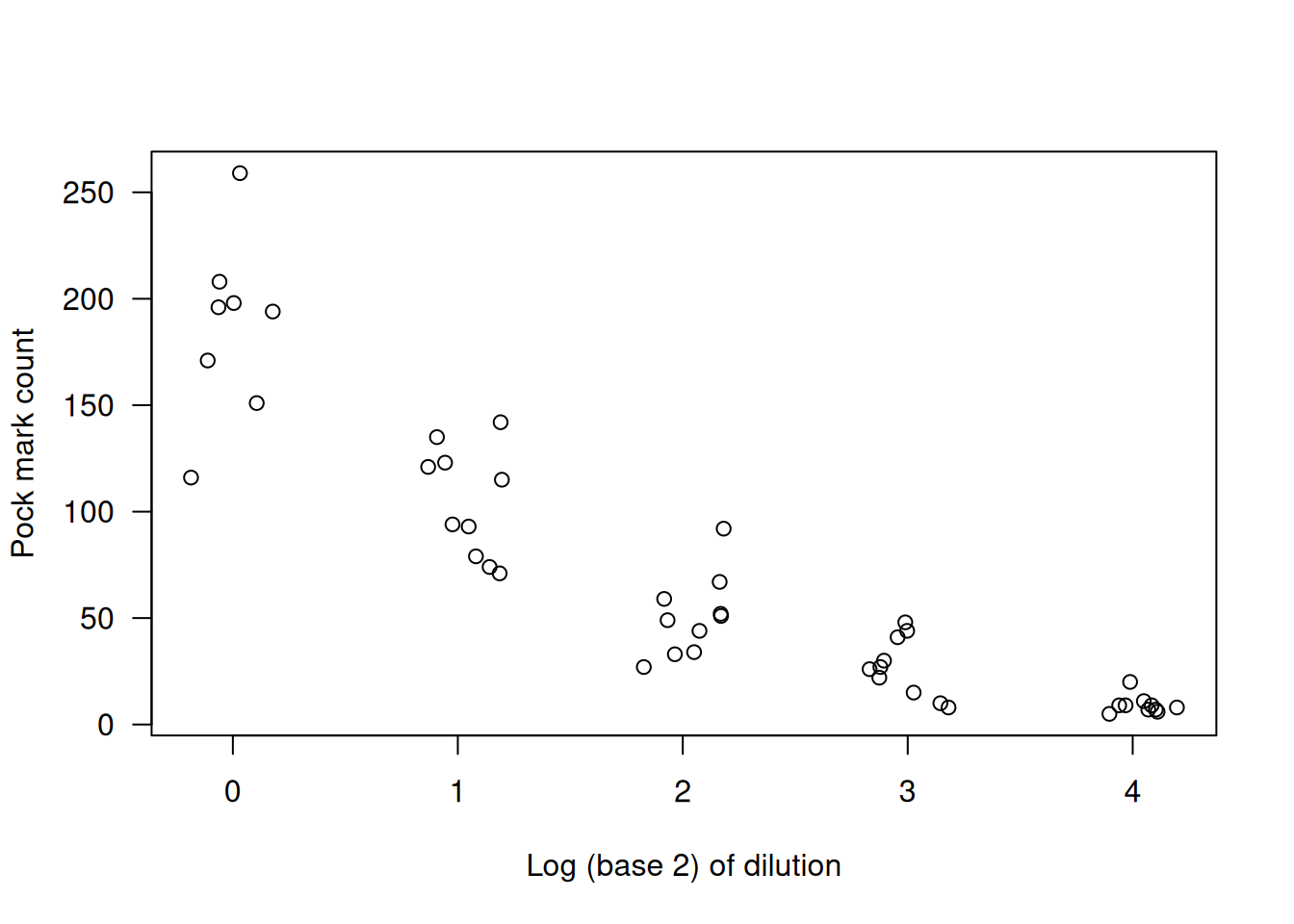

mn <- with(pock, tapply(Count, log2(Dilution), mean))
vr <- with(pock, tapply(Count, log2(Dilution), var))
plot( log(vr) ~ log(mn), las=1,
    xlab="Group mean", ylab="Group variance")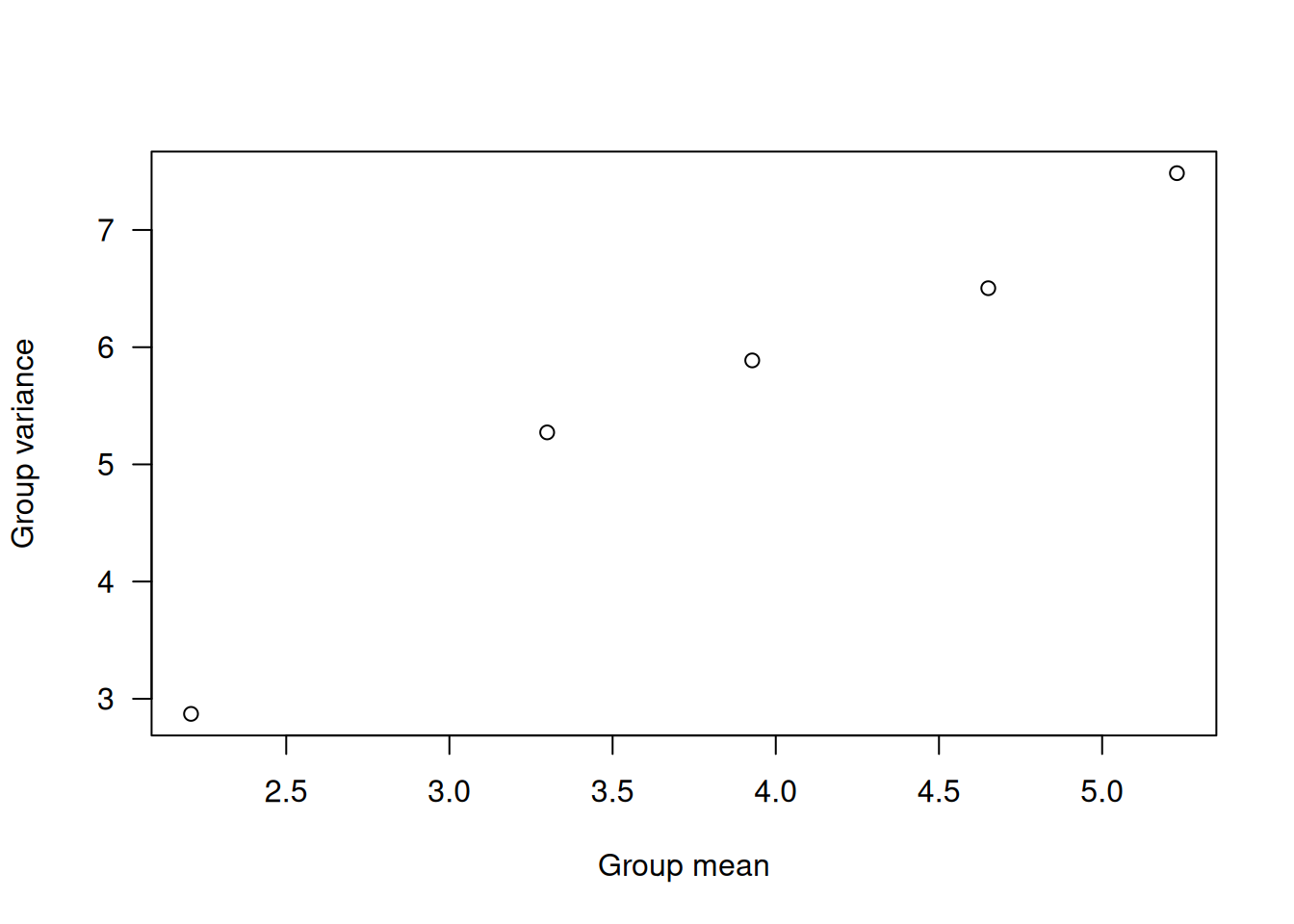

data.frame(mn, vr, ratio=vr/mn)

       mn         vr    ratio
0 186.625 1781.12500 9.543871
1 104.700  667.34444 6.373872
2  50.800  360.40000 7.094488
3  27.100  194.98889 7.195162
4   9.100   17.65556 1.940171

El cociente varianza/media supera ampliamente 1 en cada nivel y tiende a crecer con la media, sugiriendo una función de varianza aproximada \(V(\mu)=\mu^{1.5}\). Al ajustar un modelo Poisson:

m1 <- glm(Count ~ log2(Dilution), data=pock, family=poisson)
c(Df = df.residual(m1),
  Resid.Dev = deviance(m1),
  Pearson.X2 = sum(residuals(m1, type="pearson")^2))

        Df  Resid.Dev Pearson.X2 
   46.0000   290.4387   291.5915

obtenemos:

Deviance residual: 290.44 con 46 grados de libertad.
Estadístico de Pearson casi idéntico.

Estos valores, mucho mayores que sus grados de libertad, confirman la presencia de sobredispersión pese a que la aproximación saddlepoint (mínimo \(y_i=5>3\)) sea razonable. En las secciones siguientes se presentan dos estrategias para modelar este exceso de varianza.

9.4 Modelos de Regresión Binomial Negativa

En presencia de sobredispersión en un GLM de Poisson, una forma natural de introducir variabilidad extra es emplear un modelo jerárquico en el que la media de Poisson sea aleatoria. Es decir, en lugar de suponer

\[ y_i\sim\mathrm{Pois}(\mu_i), \]

planteamos

\[ y_i\mid\lambda_i\sim\mathrm{Pois}(\lambda_i),\qquad \lambda_i\sim G(\mu_i,\psi), \]

donde \(G(\mu_i,\psi)\) es una distribución con media \(\mu_i\) y coeficiente de variación \(\psi\). Bajo este planteamiento se muestra que

\[ \mathrm{E}[y_i]=\mu_i,\qquad \text{Var}[y_i]=\mu_i+\psi\,\mu_i^2, \]

incorporando así un término de sobredispersión \(\psi,\mu_i^2\).

Si se elige \(G\) como una gamma, cuyo coeficiente de variación es precisamente su parámetro de dispersión, el modelo resultante para \(y_i\) es la binomial negativa con función de probabilidad

\[ \mathcal{P}(y_i;\mu_i,k) =\frac{\Gamma(y_i+k)}{\Gamma(y_i+1)\,\Gamma(k)} \Bigl(\tfrac{\mu_i}{\mu_i+k}\Bigr)^{y_i} \Bigl(1-\tfrac{\mu_i}{\mu_i+k}\Bigr)^{k}, \]

donde \(k=1/\psi\). En este caso

\[ \text{Var}[y_i]=\mu_i+\frac{\mu_i^2}{k}, \]

y la unidad de devianza resulta

\[ d(y,\mu) =2\Bigl\{y\log\frac{y}{\mu} \;-\;(y+k)\log\frac{y+k}{\mu+k}\Bigr\}, \]

lo que confirma que la binomial negativa pertenece a la familia EDM con dispersión \(\phi=1\).

En la práctica se desconoce \(k\), por lo que en R se emplea la función glm.nb() del paquete MASS, que estima simultáneamente \(k\) (denotado theta) y los coeficientes \(\beta_j\) por máxima verosimilitud. Tras convertir el objeto con glm.convert(), el ajuste se trata como un GLM con \(\phi=1\).

Los modelos binomiales negativos tienden a proporcionar errores estándares mayores que el Poisson (en función de \(k\)), aunque los \(\hat\beta_j\) suelen ser comparables. Por convención, el enlace logarítmico es el habitual para garantizar \(\mu>0\). Al igual que en otros GLMs de conteo, se recomiendan residuos cuantil para diagnóstico (Sect. 8.3.4.2), que tienden a comportarse mejor en presencia de sobredispersión.

Ejemplo

En los datos de pock se observa sobredispersión respecto al modelo de Poisson . Para acomodar esa variabilidad extra, se ajusta un GLM binomial negativo estimando el parámetro de dispersión inverso \(k\) mediante la función glm.nb() del paquete MASS, que devuelve:

library(MASS)
m.nb <- glm.nb(Count ~ log2(Dilution), data = pock)
m.nb$theta  # theta equivale a k

[1] 9.892894

# [1] 9.892894

Aquí \(k\approx9.89\), lo que implica una función de varianza

\[ V(\mu)\approx \mu + \frac{\mu^2}{k}\approx \mu + 0.10\,\mu^2, \]

y un coeficiente de variación de la distribución de mezcla \(\psi=1/k\approx0.10\).

Tras convertir el objeto a estilo de GLM convencional con glm.convert(), fijando \(\phi=1\), el resumen de los coeficientes es:

printCoefmat(coef(summary(m.nb, dispersion=1)))

               Estimate Std. Error z value  Pr(>|z|)    
(Intercept)     5.33284    0.08786  60.697 < 2.2e-16 ***
log2(Dilution) -0.72460    0.03886 -18.646 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

printCoefmat(coef( summary(m1)) )

                Estimate Std. Error z value  Pr(>|z|)    
(Intercept)     5.267932   0.022552 233.596 < 2.2e-16 ***
log2(Dilution) -0.680944   0.015443 -44.093 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comparado con el modelo de Poisson, cuyos coeficientes son similares pero con errores estándar mucho menores (p.ej. \(0.0226\) vs. \(0.0879\) para el intercepto), el binomial negativo refleja la sobredispersión inflando los errores y dando inferencias más conservadoras.

Los gráficos de diagnóstico (residuos cuantil vs. valores ajustados, diagramas de Cook, Q–Q) muestran un ajuste adecuado sin observaciones influyentes destacables, lo que confirma que el modelo binomial negativo capta correctamente la variabilidad extra presente en los datos.

9.5 Modelos cuasi-Poisson

Cuando los conteos presentan sobredispersión relativa al modelo Poisson (\(\text{var}[y_i]=\mu_i\)), una solución sencilla es el modelo cuasi-Poisson, que conserva la función de varianza \(V(\mu)=\mu\) pero introduce un parámetro de dispersión \(\phi>1\) tal que

\[ \text{var}[y_i] = \phi\,\mu_i. \]

Este modelo puede justificarse de manera análoga a los modelos cuasi-binomiales: si contamos eventos en poblaciones grandes cuyos individuos están correlacionados positivamente, la varianza real supera a la de Poisson y puede aproximarse por \(\phi\mu_i\). Aunque no existe una distribución de masa de probabilidad con esta varianza, la teoría de cuasi-verosimilitud garantiza que los estimadores de los \(\beta_j\) y sus errores estándar sean consistentes siempre que \(\text{E}[y_i]=\mu_i\) y \(\text{var}[y_i]=\phi\mu_i\) estén bien especificados.

Las estimaciones de los coeficientes \(\hat\beta_j\) coinciden con las de un Poisson GLM, pero los errores estándar se escalan por \(\sqrt{\phi}\), ampliando los intervalos de confianza y moderando los valores \(P\). En R, basta con usar:

m.qp <- glm( Count ~ log2(Dilution),
             data = pock,
             family = quasipoisson() )

Para comparar el ajuste con el Poisson, podemos examinar la razón de los errores estándar:

se.pois <- coef(summary(m1))[ , "Std. Error"]
se.qp   <- coef(summary(m.qp))[ , "Std. Error"]
data.frame(SE.Pois = se.pois,
           SE.Quasi = se.qp,
           Ratio    = se.qp / se.pois)

                  SE.Pois   SE.Quasi    Ratio
(Intercept)    0.02255150 0.05677867 2.517733
log2(Dilution) 0.01544348 0.03888257 2.517733

# Estimación de phi
sqrt( summary(m.qp)$dispersion )

[1] 2.517733

En este caso, el ajuste cuasi-Poisson al conjunto pock muestra \(\sqrt{\hat\phi}\approx 2.52\), lo que indica que los errores estándar se inflan en ese factor. Los diagnósticos (residuos deviance estandarizados, distancia de Cook, etc.) sugieren que el modelo cuasi-Poisson es adecuado, aunque no permite calcular residuales de cuantiles ni AIC por carecer de distribución de probabilidad explícita:

library(statmod)

# Suponemos que m.qp es nuestro modelo cuasi-Poisson ya ajustado:
# m.qp <- glm( Count ~ log2(Dilution), data = pock, family = quasipoisson() )

# 1. Residuos cuantílicos (aproximados usando la familia Poisson)
qr_qp <- qresid(m.qp)  

# 2. Residuos deviance estandarizados
rstd_qp <- rstandard(m.qp)

# 3. Distancia de Cook
cook_qp <- cooks.distance(m.qp)

# Configuramos la gráfica en una fila de tres columnas
par(mfrow = c(3, 1), las = 1, mar = c(4, 4, 2, 1))

# Gráfico 1: residuos cuantílicos
plot(qr_qp, 
     ylab = "Residuos cuantílicos", 
     xlab = "Índice de observación", 
     main = "Quantile residuals")

# Gráfico 2: residuos deviance estandarizados
plot(rstd_qp, 
     ylab = "Residuos estandarizados", 
     xlab = "Índice de observación", 
     main = "Standardized deviance residuals")

# Gráfico 3: distancia de Cook
plot(cook_qp, type = "h",
     ylab = "Distancia de Cook", 
     xlab = "Índice de observación", 
     main = "Cook's distance")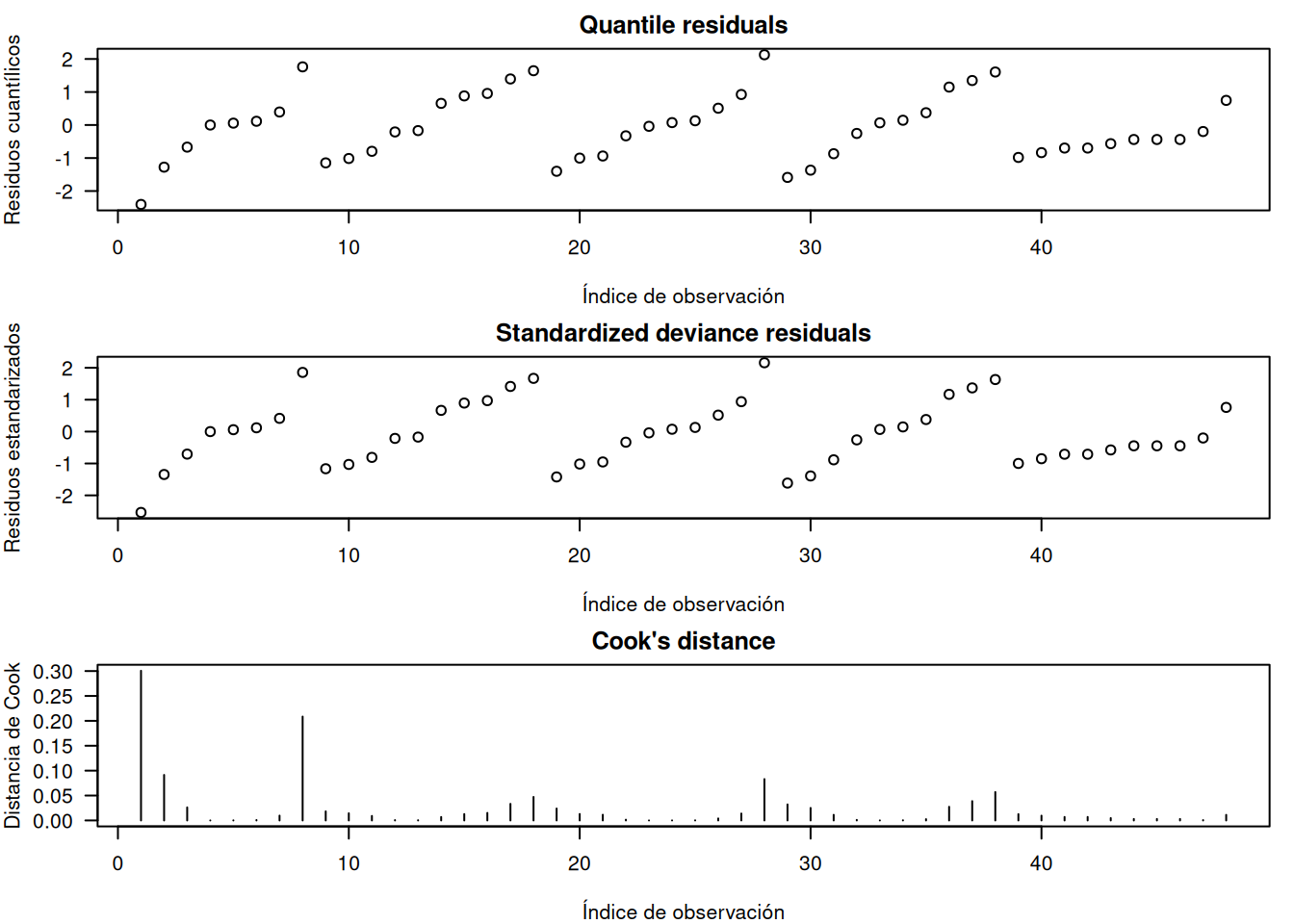

Ventajas

Fácil de implementar con glm(..., family=quasipoisson()).

Ajusta la sobredispersión sin cambiar la estructura multiplicativa del Poisson.

Limitaciones

No define una distribución de probabilidad completa (no hay AIC).

Supone una varianza lineal en \(\mu\), que puede no ajustarse tan bien como el modelo binomial negativo si la sobredispersión crece más rápido que \(\mu\).