14 Modelo de Riesgos Proporcionales: Diagnósticos

14.1 Evaluación del ajuste mediante residuos

En regresión lineal, los residuos permiten diagnosticar y corregir malas especificaciones. En supervivencia, debido al proceso de conteo y al supuesto de riesgos proporcionales, se han desarrollado residuos específicos que ayudan a evaluar el ajuste del modelo de Cox y, en algunos casos, a sugerir transformaciones.

14.1.1 Residuos de martingala y de devianza

Residuo de martingala para el sujeto \(i\): \[ m_i \;=\;\delta_i \;-\;\widehat H_0(t_i)\,\exp\bigl(z_i^\top\hat\beta\bigr), \] donde
- \(\delta_i\in\{0,1\}\) indica censura (0) o muerte (1),
- \(\widehat H_0(t)\) es la tasa de riesgo acumulada estimada,
- \(\exp(z_i^\top\hat\beta)\) el factor de riesgo.
Cumplen \(\mathbb E[m_i]=0\), \(\sum_i m_i=0\) y \(m_i\in(-\infty,1]\). Su asimetría permite, mediante gráficos \(m_i\) vs. covariable, revelar la forma funcional adecuada (p.e. lineal, logarítmica, polinómica).
Residuo de devianza: \[ d_i \;=\;\mathrm{sign}(m_i)\;\sqrt{-2\bigl[m_i + \delta_i\,\log(\delta_i - m_i)\bigr]}\,. \] Es simétrico, \(\mathbb E[d_i]=0\) y \(\sum_i d_i^2\) equivale a un estadístico de devianza análogo al de GLM, útil como medida global de ajuste. Sin embargo, no aporta información sobre la forma de las covariables, por lo que en la práctica se prefieren los residuos de martingala para el diagnóstico funcional.

14.1.1.1 Ejemplo: uso de residuos de martingala en `pharmacoSmoking`

Ajustamos el modelo nulo (sin covariables) y extraemos residuos de martingala:

library(survival)
library(asaur)

result0 <- coxph(Surv(ttr, relapse) ~ 1, data = pharmacoSmoking)
rr0     <- residuals(result0, type = "martingale")

Para cada posible predictor continuo (p.e. age, priorAttempts, longestNoSmoke) graficamos \(rr_0\) vs. la variable y su transformación logarítmica, ajustando un suavizado loess:

smoothSEcurve <- function(yy, xx) {
# use after a call to "plot"
# fit a lowess curve and 95% confidence interval curve
# make list of x values
xx.list <- min(xx) + ((0:100)/100)*(max(xx) - min(xx))
# Then fit loess function through the points (xx, yy)
# at the listed values
yy.xx <- predict(loess(yy ~ xx), se=T,
newdata=data.frame(xx=xx.list))
lines(yy.xx$fit ~ xx.list, lwd=2)
lines(yy.xx$fit -
qt(0.975, yy.xx$df)*yy.xx$se.fit ~ xx.list, lty=2)
lines(yy.xx$fit +
qt(0.975, yy.xx$df)*yy.xx$se.fit ~ xx.list, lty=2)
}

attach(pharmacoSmoking)

priorAttemptsT <- priorAttempts
priorAttemptsT[priorAttempts > 20] <- 20
result.0.coxph <- coxph(Surv(ttr, relapse) ~ 1)
rr.0 <- residuals(result.0.coxph, type="martingale")

par (mfrow=c (3,2))
plot(rr.0 ~ age)
smoothSEcurve(rr.0, age)
title("Martingale residuals\nversus age")
logAge <- log(age)
plot(rr.0 ~ logAge)
smoothSEcurve(rr.0, logAge)
title("Martingale residuals\nversus log age")

plot(rr.0 ~ priorAttemptsT)
smoothSEcurve(rr.0, priorAttemptsT)
title("Martingale residuals versus\nprior attempts")
logPriorAttemptsT <- log(priorAttemptsT + 1)
plot(rr.0 ~ logPriorAttemptsT)
smoothSEcurve(rr.0, logPriorAttemptsT)
title("Martingale residuals versus\nlog prior attempts")
plot(rr.0 ~ longestNoSmoke)
smoothSEcurve(rr.0, longestNoSmoke)
title("Martingale residuals versus\n
+ longest period without smoking")
logLongestNoSmoke <- log(longestNoSmoke+1)
plot(rr.0 ~ logLongestNoSmoke)
smoothSEcurve(rr.0, logLongestNoSmoke)
title("Martingale residuals versus\n
+ log of longest period without smoking")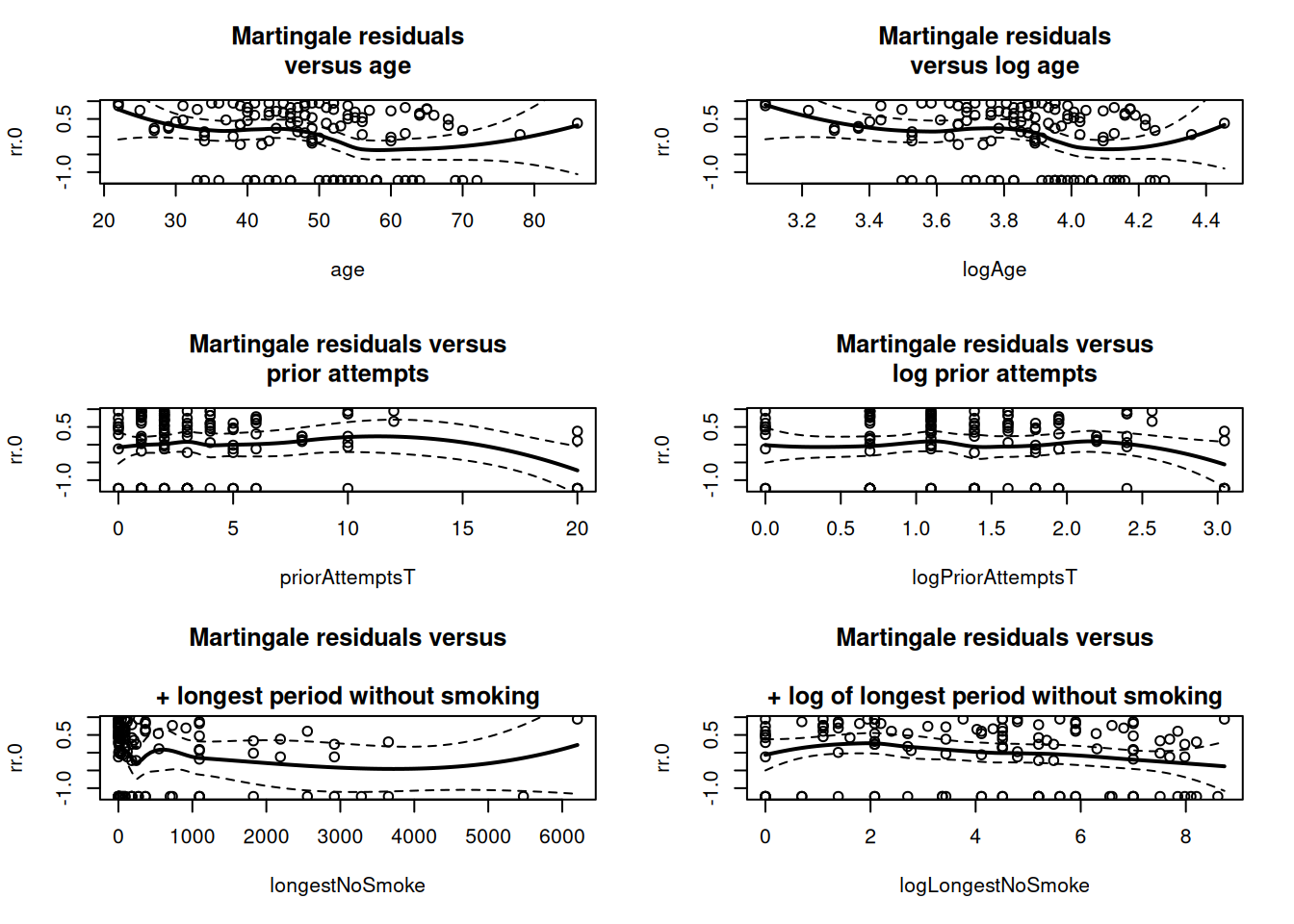

Interpretación

Las gráficas sin transformar muestran curvas no lineales, indicando que conviene investigar transformaciones (p.e. \(\log\)).
El patrón \(rr_0\) vs. edad reproduce la relación no lineal que se puede ajustar con splines como se muestra en la Sect. 6.5 del Moore.
Para longestNoSmoke, la escala logarítmica produce un patrón más lineal.

Para obtener un modelo parsimonioso que equilibre ajuste y complejidad, se parte del modelo con la sola covariable grp y se aplica la función step() indicando como alcance (scope) las siguientes variables:

result.grp.coxph <- coxph(Surv(ttr, relapse) ~ grp)
result.step <- step(result.grp.coxph, scope=list(upper=~ grp +
    gender + race + employment + yearsSmoking +
    levelSmoking + age + priorAttemptsT +
    logLongestNoSmoke, lower=~grp) )

Start:  AIC=766.32
Surv(ttr, relapse) ~ grp

                    Df    AIC
+ age                1 762.48
+ logLongestNoSmoke  1 765.19
+ yearsSmoking       1 765.76
<none>                 766.32
+ employment         2 767.24
+ gender             1 767.43
+ priorAttemptsT     1 767.63
+ levelSmoking       1 768.27
+ race               3 770.72

Step:  AIC=762.48
Surv(ttr, relapse) ~ grp + age

                    Df    AIC
+ employment         2 758.28
+ logLongestNoSmoke  1 761.99
<none>                 762.48
+ yearsSmoking       1 764.12
+ gender             1 764.20
+ priorAttemptsT     1 764.28
+ levelSmoking       1 764.48
- age                1 766.32
+ race               3 766.52

Step:  AIC=758.28
Surv(ttr, relapse) ~ grp + age + employment

                    Df    AIC
<none>                 758.28
+ logLongestNoSmoke  1 758.55
+ yearsSmoking       1 759.80
+ priorAttemptsT     1 759.87
+ gender             1 760.27
+ levelSmoking       1 760.28
+ race               3 761.10
- employment         2 762.48
- age                1 767.24

Modelo final:

La búsqueda con AIC seleccionó cuatro covariables:

grppatchOnly: comparación parche vs terapia triple
age: edad en años
employmentother: empleo “otro” vs tiempo completo
employmentpt: medio tiempo vs tiempo completo

Los coeficientes estimados (log–hazard ratios), sus exponenciales y pruebas Wald fueron:

Covariable	coef	exp(coef)	se(coef)	z	p
grppatchOnly	0.6079	1.837	0.2184	2.78	0.0054
age	–0.0353	0.965	0.0108	–3.28	0.0010
employmentother	0.7035	2.021	0.2693	2.61	0.0090
employmentpt	0.6537	1.923	0.3273	2.00	0.0460

La prueba de razón de verosimilitudes conjunta dio

\[ \chi^2=22\quad(df=4),\quad p=0.000198 \]

con \(n=125\) y 89 eventos, confirmando que el modelo mejora significativamente al nulo.

summary(result.step)

Call:
coxph(formula = Surv(ttr, relapse) ~ grp + age + employment)

  n= 125, number of events= 89 

                    coef exp(coef) se(coef)      z Pr(>|z|)   
grppatchOnly     0.60788   1.83654  0.21837  2.784  0.00537 **
age             -0.03529   0.96533  0.01075 -3.282  0.00103 **
employmentother  0.70348   2.02077  0.26929  2.612  0.00899 **
employmentpt     0.65369   1.92262  0.32732  1.997  0.04581 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                exp(coef) exp(-coef) lower .95 upper .95
grppatchOnly       1.8365     0.5445    1.1971    2.8176
age                0.9653     1.0359    0.9452    0.9859
employmentother    2.0208     0.4949    1.1920    3.4256
employmentpt       1.9226     0.5201    1.0122    3.6518

Concordance= 0.638  (se = 0.03 )
Likelihood ratio test= 22.03  on 4 df,   p=2e-04
Wald test            = 21.91  on 4 df,   p=2e-04
Score (logrank) test = 22.48  on 4 df,   p=2e-04

Se extraen los residuos de martingala del modelo final:

rr.final <- residuals(result.step, type="martingale")

Y se trazan frente a las covariables seleccionadas:

par (mfrow=c (2,2))
plot(rr.final ~ age)
smoothSEcurve(rr.final, age)
title("Martingale residuals\nversus age")
plot(rr.final ~ grp)
title("Martingale residuals\nversus treatment group")
plot(rr.final ~ employment)
title("Martingale residuals\nversus employment")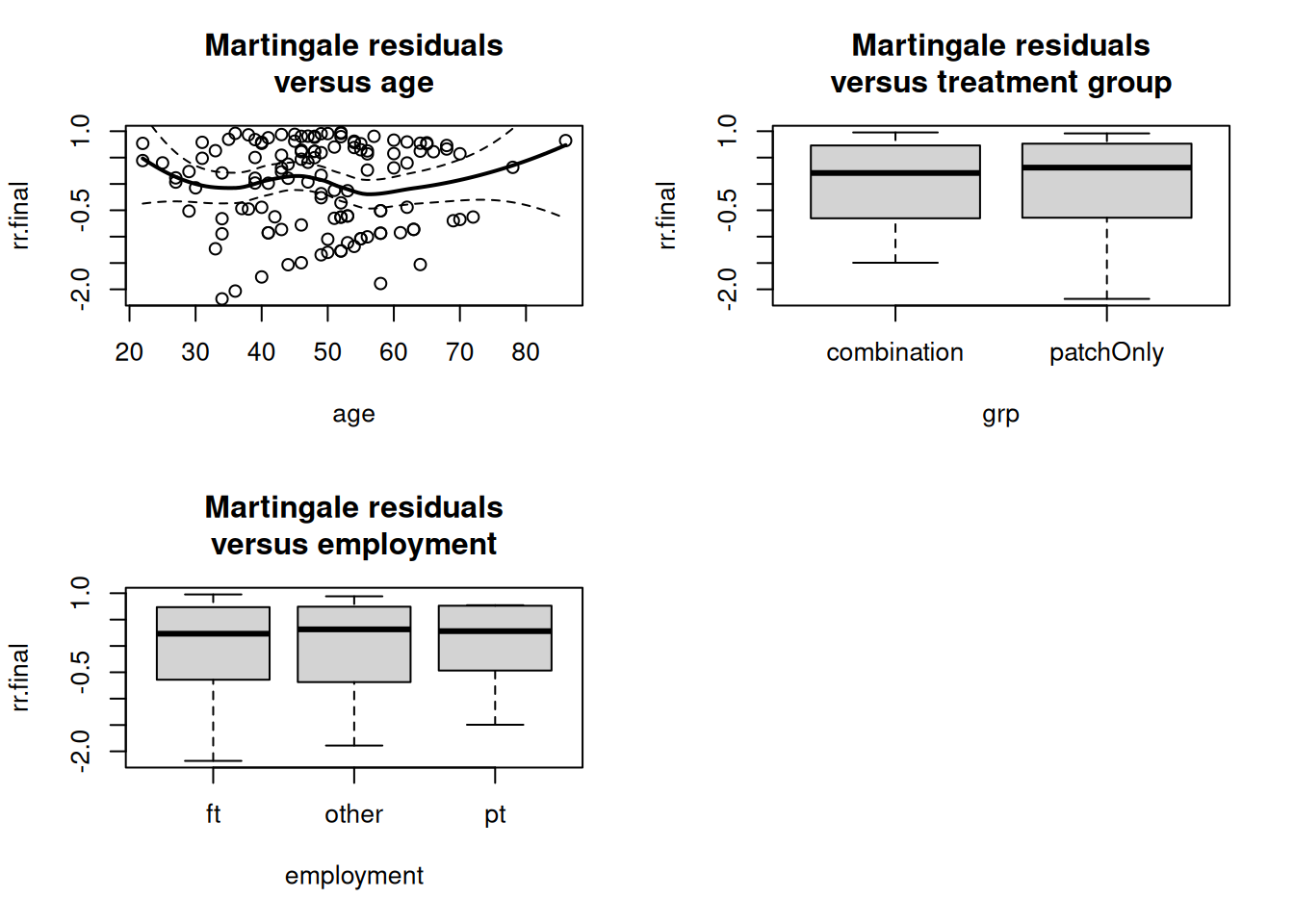

Edad: muestra poca tendencia remanente, muy mejorada respecto al modelo sin covariables.
Grupo de tratamiento (grp): residuos dispersos sin patrón, indicando buen ajuste.
Empleo (employment): igualmente bien distribuidos.

Este análisis confirma que, tras la selección por AIC, el modelo captura adecuadamente las principales fuentes de variación en el riesgo de recaída.

14.1.2 Residuales de eliminación de casos (Jackknife / dfbeta)

Los residuos de eliminación de casos miden la influencia de cada observación sobre un coeficiente concreto del modelo de Cox. En este ejemplo usamos la variable age (cuarta posición en el vector de coeficientes) para ilustrar dos formas de obtenerlos.

Primero, el método “bruto” (jackknife), que reestima el modelo \(n\) veces, excluyendo sucesivamente cada sujeto:

library(survival)

# 1. Ajustar el modelo completo y extraer coeficiente para "age"
result.coxph <- coxph(Surv(ttr, relapse) ~ grp + employment + age, data=pharmacoSmoking)
coef.all    <- result.coxph$coef["age"]

# 2. Calcular residuos jackknife
n.obs      <- nrow(pharmacoSmoking)
jkbeta.vec <- numeric(n.obs)
for(i in seq_len(n.obs)) {
  dat.i       <- pharmacoSmoking[-i, ]
  fit.i       <- coxph(Surv(ttr, relapse) ~ grp + employment + age, data=dat.i)
  coef.i      <- fit.i$coef["age"]
  jkbeta.vec[i] <- coef.all - coef.i
}

# 3. Graficar cambios en coeficiente
plot(jkbeta.vec, type="h",
     xlab="Índice de observación", ylab="Δ coeficiente para edad",
     main="Residuales jackknife (dfbeta exacto)")
abline(h=0, lty=2)
identify(jkbeta.vec)  # permite señalar puntos influyentes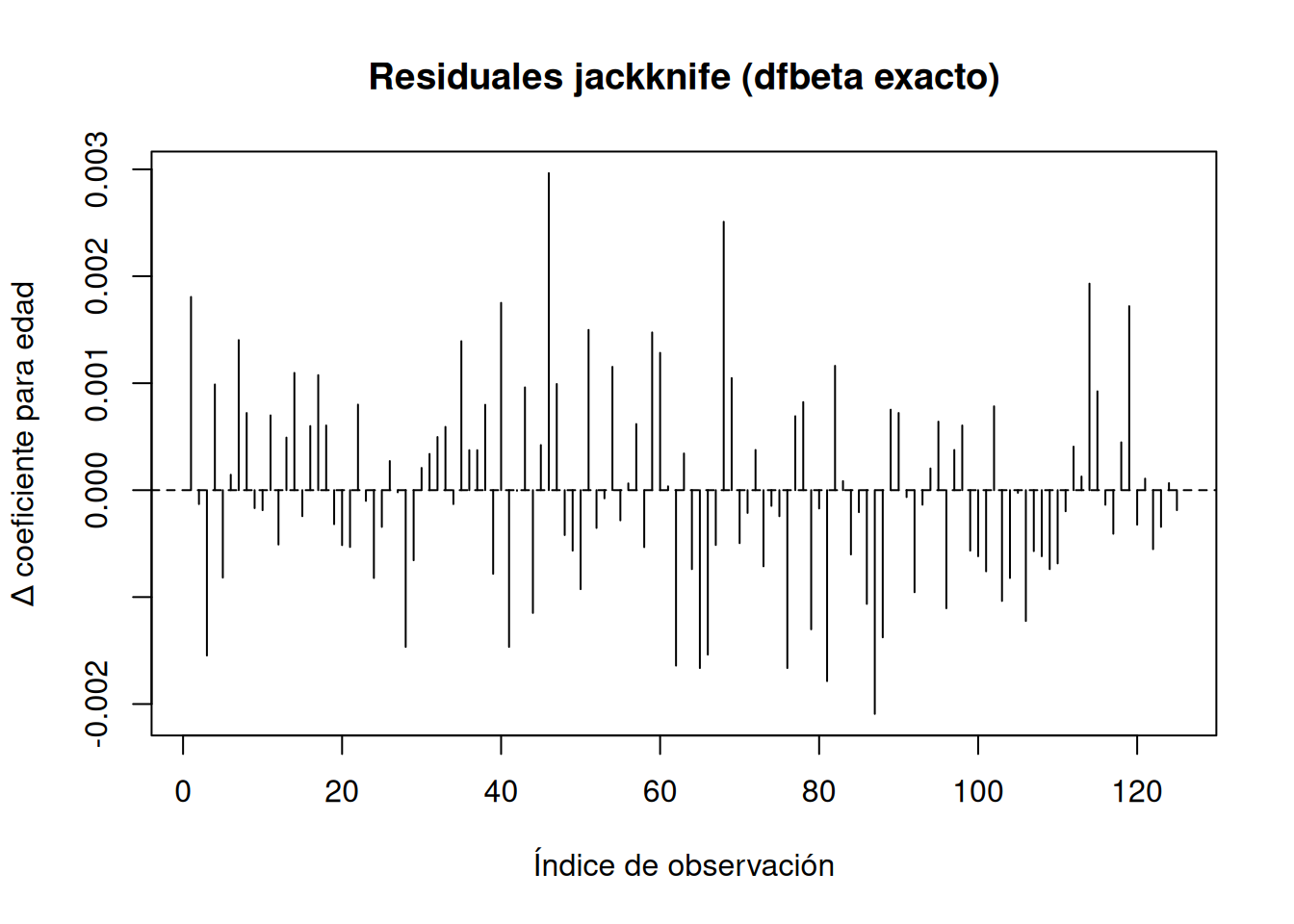

integer(0)

A continuación, la versión aproximada que sólo itera una vez a partir de \(\beta=0\), mucho más rápida:

# Residuos dfbeta aproximados vía residuals()
resid.dfbeta <- residuals(result.coxph, type="dfbeta")

# Graficar el componente correspondiente a "age"
plot(resid.dfbeta[, 4], type="h",
     xlab="Índice de observación", ylab="dfbeta para edad",
     main="Residuales dfbeta (aproximados)")
abline(h=0, lty=2)
identify(resid.dfbeta[,4])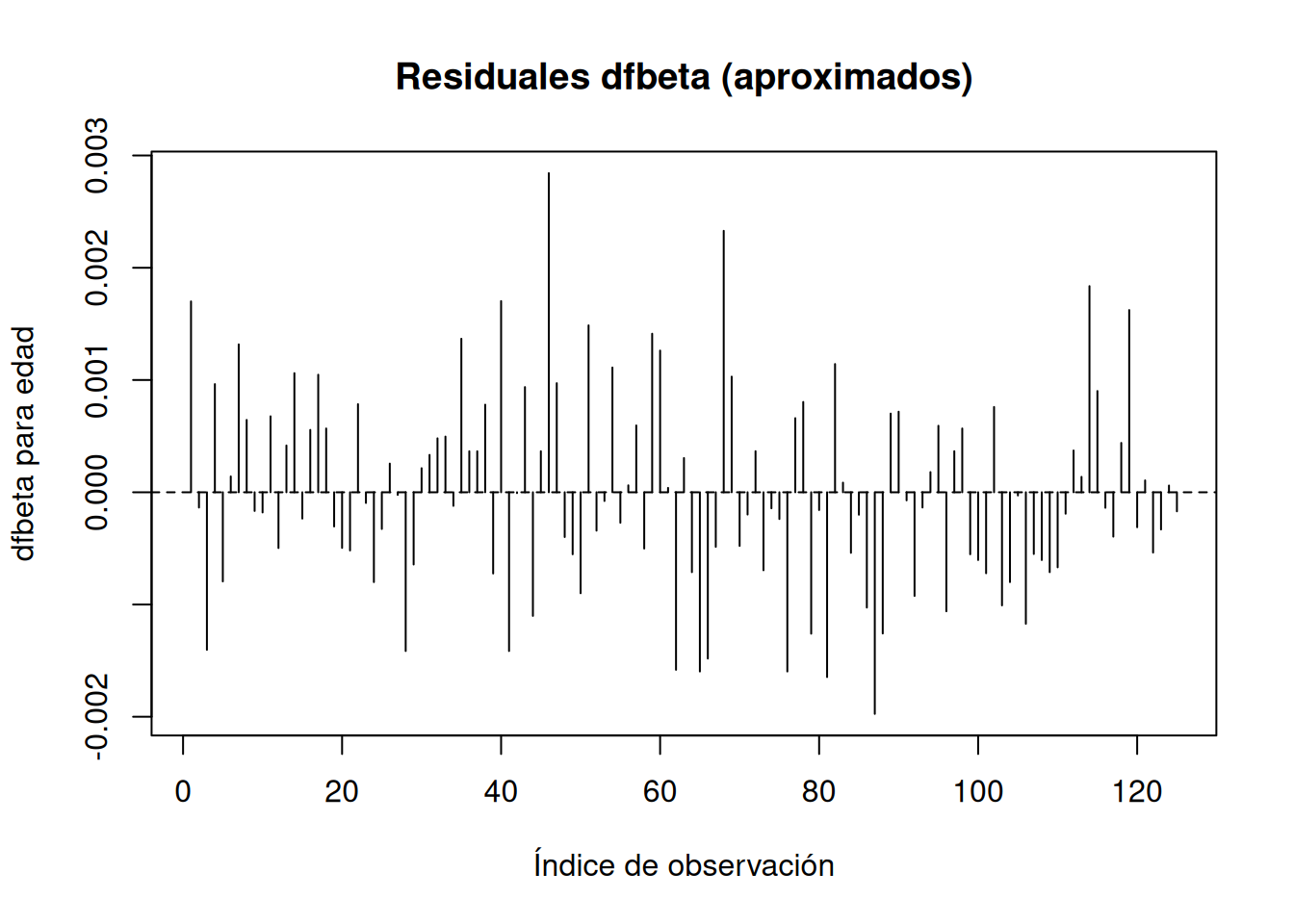

integer(0)

Y, si se desea la versión estandarizada:

# Residuos dfbetas (estandarizados)
resid.dfbetas <- residuals(result.coxph, type="dfbetas")
plot(resid.dfbetas[, 4], type="h",
     xlab="Índice de observación", ylab="dfbetas para edad",
     main="Residuales dfbetas (estandarizados)")
abline(h=0, lty=2)
identify(resid.dfbetas[, 4])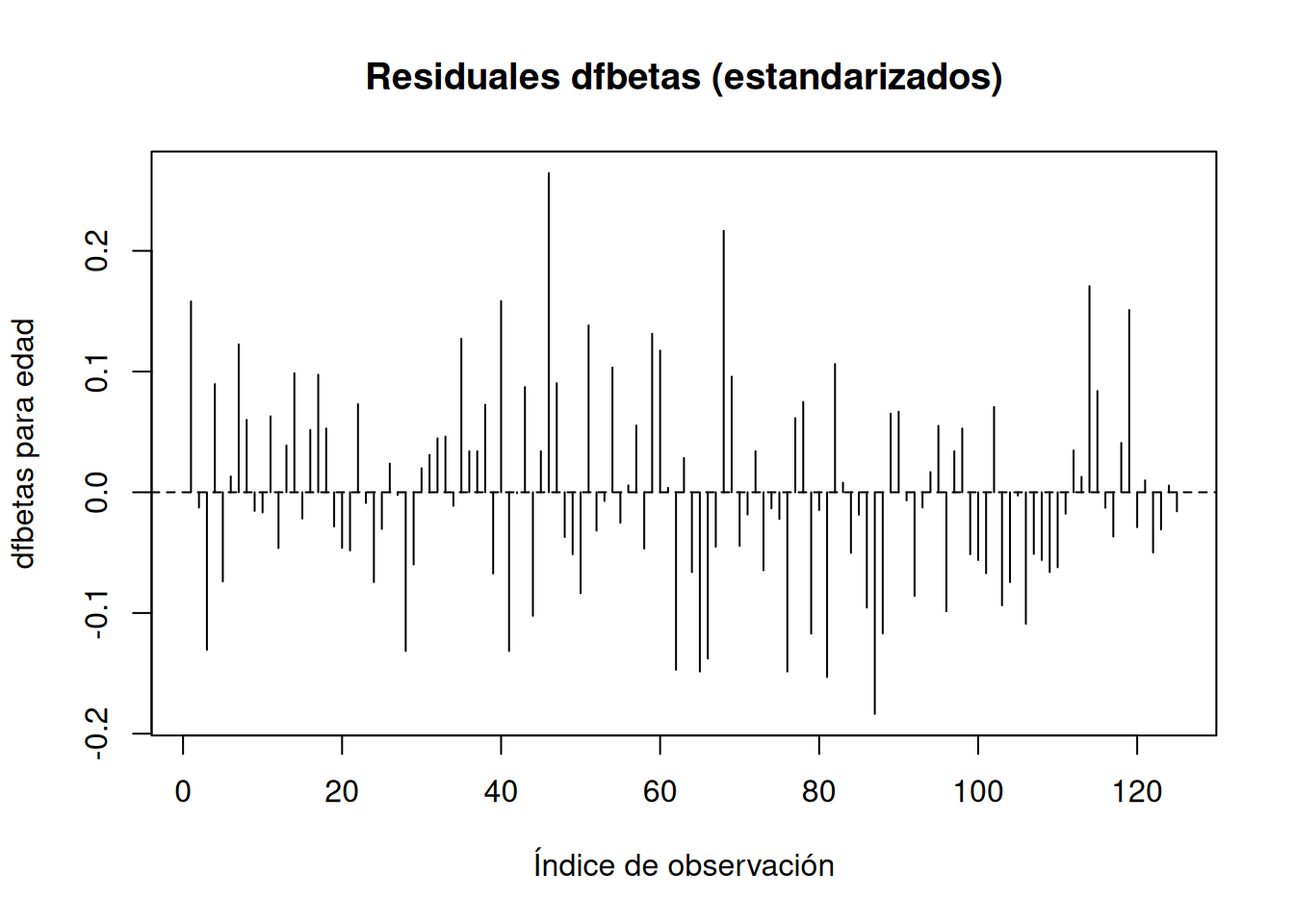

integer(0)

En cada caso, picos destacados revelan observaciones que tienen un efecto desproporcionado sobre el estimador de la pendiente para age.

14.2 Comprobación de la hipótesis de riesgos proporcionales

La suposición de riesgos proporcionales es fundamental en el modelo de Cox, pues permite cancelar la función de riesgo basal del partial likelihood. Para un covariable binaria (tratamiento vs. control), implica que las funciones de riesgo satisfacen

\[ h_1(t)=e^{\beta}\,h_0(t) \]

y, por tanto, las curvas de log-riesgo acumulado deben ser paralelas. Aunque pequeñas desviaciones suelen tener un impacto mínimo en los parámetros estimados, es conveniente evaluar esta suposición.

14.2.1 Gráficos de log-log complementario

Bajo riesgos proporcionales, las funciones de supervivencia cumplen

\[ S_1(t)=\bigl[S_0(t)\bigr]^{e^{\beta}}. \]

Tomando la transformación complementaria log-log,

\[ \log\bigl\{-\log S_1(t)\bigr\} =\beta+\log\bigl\{-\log S_0(t)\bigr\}, \]

la cual se extiende de \((0,1)\) a \((-\infty,\infty)\). Un gráfico de

g(u) = log(-log(u))

frente a \(\log(t)\) debe mostrar dos trazos paralelos separados por \(\beta\) si la suposición se cumple.

A modo de ejemplo, con los datos de cáncer de páncreas:

library(survival)

attach(pancreatic)
Progression.d  <- as.Date(progression, "%m/%d/%Y")
OnStudy.d      <- as.Date(onstudy,     "%m/%d/%Y")
Death.d        <- as.Date(death,       "%m/%d/%Y")
progrSurv      <- Progression.d - OnStudy.d
overallSurv    <- Death.d       - OnStudy.d
pfs            <- pmin(progrSurv, overallSurv)
pfs[is.na(pfs)] <- overallSurv[is.na(pfs)]
pfs.month      <- as.numeric(pfs) / 30.5

# Ajuste Kaplan–Meier por estadío
km.LA <- survfit(Surv(pfs.month) ~ 1, subset=(stage=="LA"), data=pancreatic)
km.M  <- survfit(Surv(pfs.month) ~ 1, subset=(stage=="M"),  data=pancreatic)

# Transformación complementaria log-log
cll.LA <- log(-log(km.LA$surv))
cll.M  <- log(-log(km.M$surv))

# Gráfico vs. log(t)
plot(cll.LA ~ log(km.LA$time), type="s", col="blue", lwd=2,
     xlab="Log(tiempo en meses)", ylab="Log(-log(S))")
lines(cll.M ~ log(km.M$time), col="red", lwd=2, type="s")
legend("bottomright", legend=c("LAPC","MPC"), col=c("blue","red"), lwd=2)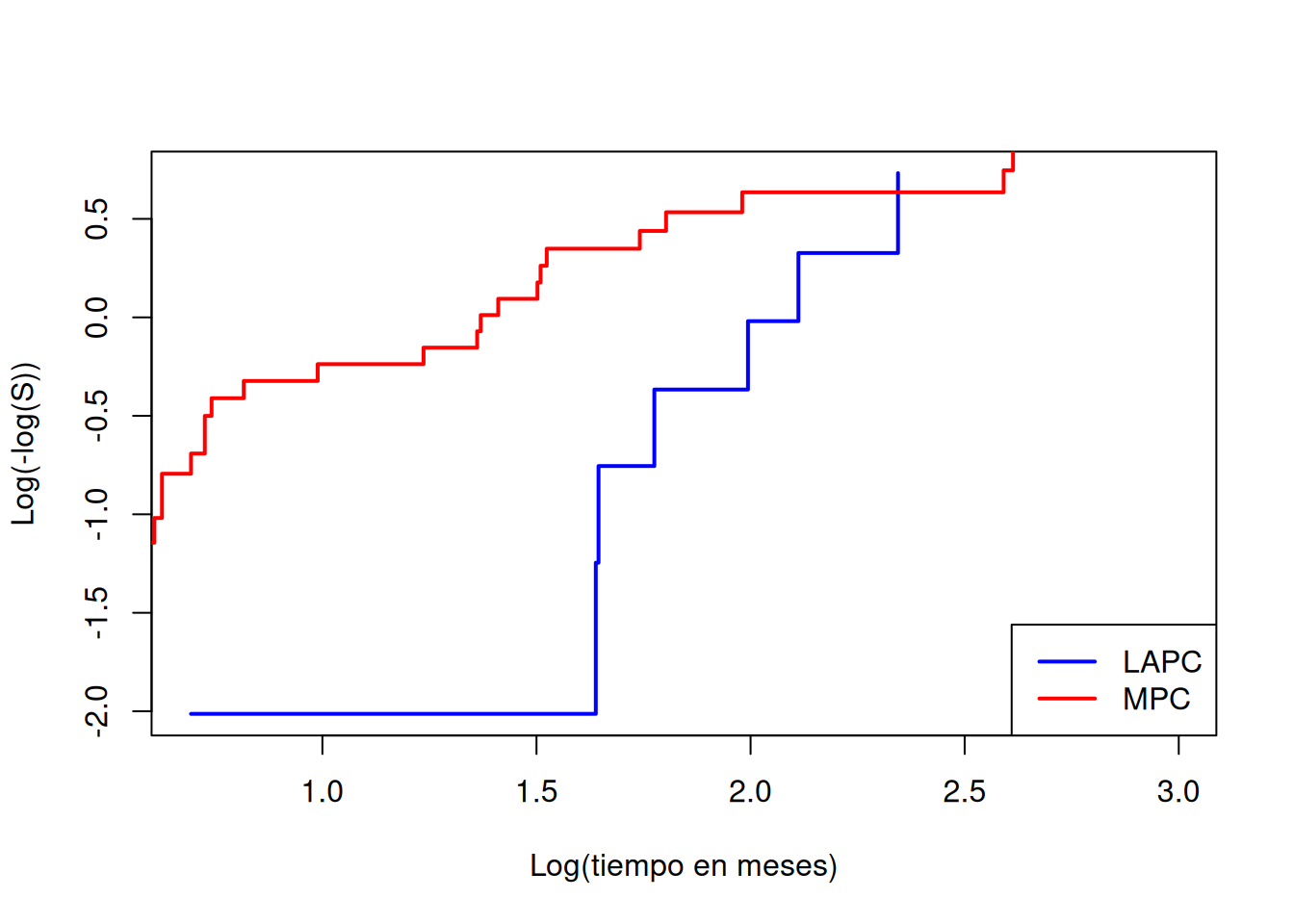

En la figura anterior, las curvas no son paralelas, lo que sugiere una violación de la hipótesis de riesgos proporcionales. Dado el tamaño de muestra reducido, no existe un contraste formal sencillo aquí, pero este gráfico aporta una valiosa evaluación visual.

14.2.2 Residuos de Schoenfeld

Los residuos de Schoenfeld ofrecen una herramienta gráfica y numérica para evaluar la hipótesis de riesgos proporcionales en un modelo de Cox. Se derivan de la función de log-verosimilitud parcial

\[ l(\beta)=\sum_{i\in D}\Bigl[z_i'\beta-\log\!\bigl(\sum_{k\in R_i}e^{z_k'\beta}\bigr)\Bigr], \]

cuyo derivada (función de “score”) es

\[ l'(\beta)=\sum_{i\in D}\Bigl[z_i-\sum_{k\in R_i}z_k\,p(\beta,z_k)\Bigr], \] donde

\[ p(\beta,z_k)=\frac{e^{z_k'\beta}}{\sum_{j\in R_i}e^{z_j'\beta}}\] Para cada tiempo de falla \(t_i\), el residual de Schoenfeld es

\[ \hat r_i \;=\; z_i \;-\;\bar z(t_i), \quad \bar z(t_i)=\sum_{k\in R_i} z_k\,p(\hat\beta,z_k), \]

es decir, la covariable observada menos su valor “esperado” en el conjunto en riesgo en \(t_i\). Bajo riesgos proporcionales, los puntos \(\hat r_i\) deben dispersarse alrededor de cero sin tendencia.

A continuación tienes el resumen solicitando, conservando el código R tal cual:

Los residuos de Schoenfeld escalados (Grambsch y Therneau) se definen como

\[ r_{i}^{*}=r_{i}\;\cdot\;d\;\cdot\operatorname{var}(\hat\beta) \]

donde \(r_{i}\) es el residuo de Schoenfeld sin escalar, \(d\) el número total de muertes y \(\operatorname{var}(\hat\beta)\) la varianza (o matriz de covarianza) del estimador \(\hat\beta\). En R:

 tt <- c(6, 7, 10, 15, 19, 25)
 delta <- c(1, 0, 1, 1, 0, 1)
 trt <- c(0, 0, 1, 0, 1, 1)
 result.coxph <- coxph(Surv(tt, delta) ~ trt)
 result.coxph$coef

      trt 
-1.326129

 resid.unscaled <- residuals(result.coxph, type="schoenfeld")
 resid.scaled   <- resid.unscaled * result.coxph$var * sum(delta)

Warning in resid.unscaled * result.coxph$var: Recycling array of length 1 in vector-array arithmetic is deprecated.
  Use c() or as.vector() instead.

 resid.unscaled

         6         10         15         25 
-0.2098004  0.5566351 -0.3468347  0.0000000

 resid.scaled

[1] -1.313064  3.483776 -2.170712  0.000000

Therneau y Grambsch demostraron que

\[ E\bigl(r_{i}^{*}\bigr)\approx \beta + \beta(t), \]

de modo que una estimación de la función de riesgo dependiente del tiempo \(\beta(t)\) se obtiene añadiendo \(\hat\beta\) a los residuos escalados:

resid.scaled + result.coxph$coef

[1] -2.639193  2.157647 -3.496841 -1.326129

La función cox.zph() automatiza estos cálculos y proporciona además una prueba de no proporcionalidad:

resid.sch <- cox.zph(result.coxph)
resid.sch$y

         trt
6  -2.639193
10  2.157647
15 -3.496841
25 -1.326129

Aplicado a los datos de cáncer de páncreas, usando tiempo transformado por Kaplan–Meier:

result.coxph      <- coxph(Surv(pfs.month) ~ stage)
result.sch.resid  <- cox.zph(result.coxph, transform="km")
plot(result.sch.resid)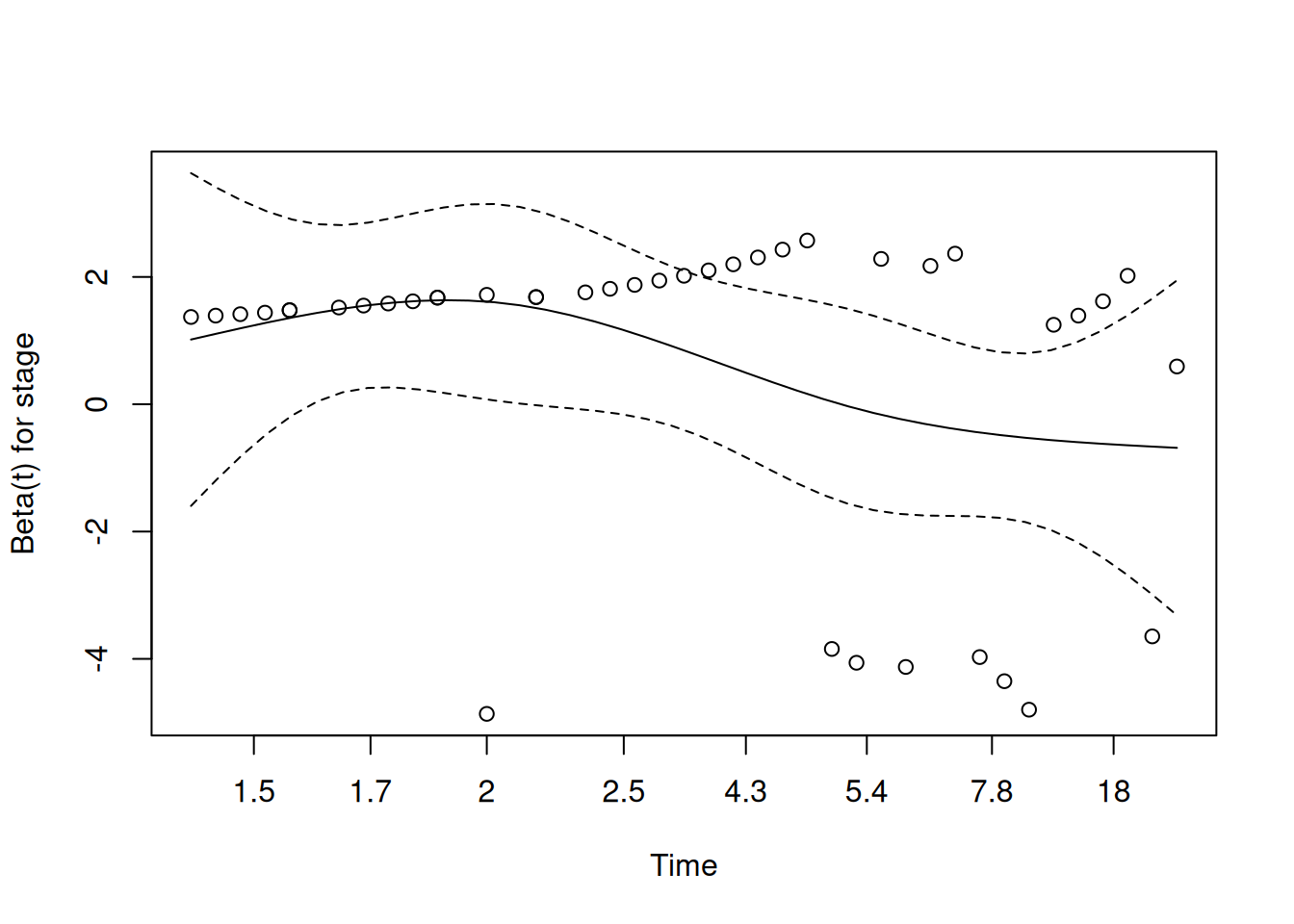

result.sch.resid

       chisq df     p
stage   4.52  1 0.034
GLOBAL  4.52  1 0.034

cox.zph(result.coxph, transform="rank")

       chisq df     p
stage   4.57  1 0.033
GLOBAL  4.57  1 0.033

cox.zph(result.coxph, transform="identity")

       chisq df    p
stage   2.32  1 0.13
GLOBAL  2.32  1 0.13

Con transform="km" (o "rank") el p-valor cercano a 0.05 sugiere violación leve de riesgos proporcionales.
Con transform="identity", al sobreponderar los tiempos tardíos escasos, el p-valor (0.239) es menos sensible a esa no uniformidad de eventos.

14.3 Covariables dependientes del tiempo

En muchos estudios de supervivencia las covariables cambian tras el inicio del seguimiento (“time-dependent covariates”), y usar su valor final para todo el periodo introduce un sesgo de predicción con información del futuro. El clásico ejemplo es el estudio de trasplante cardíaco de Stanford (Clark et al. 1971), donde un análisis ingenuo es el siguiente:

result.heart <- coxph(Surv(futime, fustat) ~ transplant + age +
+                       surgery, data=jasa)
summary(result.heart)

Call:
coxph(formula = Surv(futime, fustat) ~ transplant + age + +surgery, 
    data = jasa)

  n= 103, number of events= 75 

               coef exp(coef) se(coef)      z Pr(>|z|)    
transplant -1.71711   0.17958  0.27853 -6.165 7.05e-10 ***
age         0.05889   1.06065  0.01505  3.913 9.12e-05 ***
surgery    -0.41902   0.65769  0.37118 -1.129    0.259    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

           exp(coef) exp(-coef) lower .95 upper .95
transplant    0.1796     5.5684    0.1040     0.310
age           1.0607     0.9428    1.0298     1.092
surgery       0.6577     1.5205    0.3177     1.361

Concordance= 0.732  (se = 0.031 )
Likelihood ratio test= 45.85  on 3 df,   p=6e-10
Wald test            = 47.15  on 3 df,   p=3e-10
Score (logrank) test = 52.63  on 3 df,   p=2e-11

parece mostrar un gran beneficio del trasplante, pero en realidad sólo refleja que “vivirás más si llegas a trasplantarte”, ya que por supuesto los pacientes deben esperar (y vivir) para poder llegar a recibir un transplante.

14.3.1 Enfoque “landmark”

Se elige un tiempo fijo (p.ej. 30 días), se descartan los que mueren antes y se clasifica a los que sobreviven según hayan recibido o no trasplante antes de ese día:

ind30        <- jasa$futime >= 30
transplant30 <- (jasa$transplant == 1) & (jasa$wait.time < 30)
summary(coxph(Surv(futime, fustat) ~ transplant30 + age + surgery, data=jasa, subset=ind30))

Call:
coxph(formula = Surv(futime, fustat) ~ transplant30 + age + surgery, 
    data = jasa, subset = ind30)

  n= 79, number of events= 52 

                     coef exp(coef) se(coef)      z Pr(>|z|)  
transplant30TRUE -0.04214   0.95874  0.28377 -0.148   0.8820  
age               0.03720   1.03790  0.01714  2.170   0.0300 *
surgery          -0.81966   0.44058  0.41297 -1.985   0.0472 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                 exp(coef) exp(-coef) lower .95 upper .95
transplant30TRUE    0.9587     1.0430    0.5497    1.6720
age                 1.0379     0.9635    1.0036    1.0734
surgery             0.4406     2.2697    0.1961    0.9898

Concordance= 0.618  (se = 0.044 )
Likelihood ratio test= 9.5  on 3 df,   p=0.02
Wald test            = 8.61  on 3 df,   p=0.03
Score (logrank) test = 8.94  on 3 df,   p=0.03

El efecto del trasplante ya no es significativo (p = 0.88). Sin embargo:

¿Por qué 30 días y no 15 o 100?
Se descarta casi un 25 % de los pacientes.

14.3.2 Modelo de Cox con covariable dependiente del tiempo

En lugar de “fijar” la covariable, la modelamos como \(z_{k}(t)\) en

\[ h(t)=h_{0}(t)\,e^{z_{k}(t)\,\beta}, \]

y adaptamos la verosimilitud parcial, recalculando en cada fallo el riesgo según el estado actual:

\[ L(\beta) =\prod_{i=1}^{D} \frac{\psi_{i i}}{\sum_{k\in R_i}\psi_{k i}} \,,\quad \psi_{k i}=e^{\beta\,z_k(t_i)}\,. \]

Aquí el denominador debe recalcularse en cada tiempo de fallo \(t_i\), pues los \(z_k(t)\) pueden haber cambiado.

Con un subconjunto ilustrativo de 6 pacientes:

id          <- 1:nrow(jasa)
jasaT       <- data.frame(id, jasa)
id.simple   <- c(2, 5, 10, 12, 28, 95)
heart.simple<- jasaT[id.simple, c(1,10,9,6,11)]

Para este subconjunto, los primeros tres fallos dan lugar a los factores:

A \(t=5\): sólo un paciente ha sido trasplantado ⇒ \(\frac{1}{5 + e^\beta}.\)
A \(t=7\): sin cambios ⇒ \(\frac{1}{4 + e^\beta}.\)
A \(t=15\): dos trasplantados entre cuatro en riesgo ⇒ \(\frac{e^\beta}{2 + 2\,e^\beta}.\)

Y así hasta completar

\[ L(\beta) =\frac{1}{5+e^\beta}\, \frac{1}{4+e^\beta}\, \frac{e^\beta}{2+2e^\beta}\, \frac{1}{2+e^\beta}\, \frac{e^\beta}{1+e^\beta}\, \frac{e^\beta}{e^\beta}\,. \]

—análisis ingenuo—

summary(coxph(Surv(futime, fustat) ~ transplant, data=heart.simple))

Call:
coxph(formula = Surv(futime, fustat) ~ transplant, data = heart.simple)

  n= 6, number of events= 6 

              coef exp(coef) se(coef)     z Pr(>|z|)
transplant -1.6878    0.1849   1.1718 -1.44     0.15

           exp(coef) exp(-coef) lower .95 upper .95
transplant    0.1849      5.408    0.0186     1.838

Concordance= 0.733  (se = 0.077 )
Likelihood ratio test= 2.47  on 1 df,   p=0.1
Wald test            = 2.07  on 1 df,   p=0.1
Score (logrank) test = 2.56  on 1 df,   p=0.1

Para hacerlo bien, dividimos cada línea de tiempo en pre- y post-trasplante (formato “start–stop”) usando tmerge:

sdata <- tmerge(heart.simple, heart.simple, id=id,death   = event(futime, fustat),transpl = tdc(wait.time))
heart.simple.counting <- sdata[,-(2:5)]
heart.simple.counting

  id tstart tstop death transpl
1  2      0     5     1       0
2  5      0    17     1       0
3 10      0    11     0       0
4 10     11    57     1       1
5 12      0     7     1       0
6 28      0    70     0       0
7 28     70    71     1       1
8 95      0     1     0       0
9 95      1    15     1       1

y aplicamos coxph en modo counting process:

summary(coxph(Surv(tstart, tstop, death) ~ transpl,data=heart.simple.counting))

Call:
coxph(formula = Surv(tstart, tstop, death) ~ transpl, data = heart.simple.counting)

  n= 9, number of events= 6 

          coef exp(coef) se(coef)     z Pr(>|z|)
transpl 0.2846    1.3292   0.9609 0.296    0.767

        exp(coef) exp(-coef) lower .95 upper .95
transpl     1.329     0.7523    0.2021      8.74

Concordance= 0.5  (se = 0.082 )
Likelihood ratio test= 0.09  on 1 df,   p=0.8
Wald test            = 0.09  on 1 df,   p=0.8
Score (logrank) test = 0.09  on 1 df,   p=0.8

14.3.2.1 Aplicación al conjunto completo

Se procesan cuidadosamente las observaciones con trasplante en jasa:

tdata            <- jasa[, -c(1:4, 11:14)]
tdata$futime     <- pmax(.5, tdata$futime)
indx             <- (tdata$wait.time == tdata$futime) & !is.na(tdata$wait.time)
tdata$wait.time[indx] <- tdata$wait.time[indx] - .5

tdata$id <- seq_len(nrow(tdata))

sdata <- tmerge(
  tdata, tdata,
  id        = id,                       
  death     = event(futime, fustat),
  transpl   = tdc(wait.time)
)

jasa.counting    <- sdata[,c(7:11,2:3)]
head(jasa.counting)

  id tstart tstop death transpl surgery      age
1  1      0    49     1       0       0 30.84463
2  2      0     5     1       0       0 51.83573
3  3      0    15     1       1       0 54.29706
4  4      0    35     0       0       0 40.26283
5  4     35    38     1       1       0 40.26283
6  5      0    17     1       0       0 20.78576

y, finalmente,

summary(coxph(Surv(tstart, tstop, death) ~ transpl + surgery + age, data=jasa.counting))

Call:
coxph(formula = Surv(tstart, tstop, death) ~ transpl + surgery + 
    age, data = jasa.counting)

  n= 170, number of events= 75 

            coef exp(coef) se(coef)      z Pr(>|z|)  
transpl  0.01405   1.01415  0.30822  0.046   0.9636  
surgery -0.77326   0.46150  0.35966 -2.150   0.0316 *
age      0.03055   1.03103  0.01389  2.199   0.0279 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

        exp(coef) exp(-coef) lower .95 upper .95
transpl    1.0142     0.9860    0.5543    1.8555
surgery    0.4615     2.1668    0.2280    0.9339
age        1.0310     0.9699    1.0033    1.0595

Concordance= 0.599  (se = 0.036 )
Likelihood ratio test= 10.72  on 3 df,   p=0.01
Wald test            = 9.68  on 3 df,   p=0.02
Score (logrank) test = 10  on 3 df,   p=0.02

Conclusión: ni con todo el registro (ni con landmark ni con counting) hay evidencia de que el trasplante aumente la supervivencia, pero solo el enfoque de covariables dependientes del tiempo evita el sesgo sin desechar datos.

14.3.3 Covariables Dependientes del Tiempo “Predecibles”

Una forma de modelar violaciones a la hipótesis de riesgos proporcionales es permitir que el coeficiente de un covariable cambie con el tiempo. En lugar de

\[ h(t)=h_{0}(t)\,e^{z_k\beta}\quad\longrightarrow\quad h(t)=h_{0}(t)\,e^{z_k\,\beta(t)}, \]

definimos una nueva covariable dependiente del tiempo cuya forma funcional es fijada por el analista. A este tipo de covariable se le llama predecible.

14.3.3.1 Uso de la función de transferencia de tiempo

Retomemos los datos de cáncer de páncreas (“pancreatic2” en el paquete asaur). Primero creamos un indicador numérico del estadio:

library(survival)
stage.n <- as.integer(pancreatic2$stage == "M")
result.panc <- coxph(Surv(pfs) ~ stage.n, data = pancreatic2)
result.panc

Call:
coxph(formula = Surv(pfs) ~ stage.n, data = pancreatic2)

          coef exp(coef) se(coef)    z     p
stage.n 0.5931    1.8095   0.4007 1.48 0.139

Likelihood ratio test=2.43  on 1 df, p=0.1188
n= 41, number of events= 41

El valor p≈0.14 muestra falta de evidencia en el factor de estadío, pero un análisis previo de residuos de Schoenfeld sugirió que la razón de riesgos varía en el tiempo. Una opción es definir

\[ g(t)\;=\;z\;\log(t) \]

y usar la sintaxis tt() de survival para incorporar esta dependencia:

result.panc2.tt <- coxph(
  Surv(pfs) ~ stage.n + tt(stage.n),
  data = pancreatic2,
  tt = function(x, t, ...) x * log(t)
)
result.panc2.tt

Call:
coxph(formula = Surv(pfs) ~ stage.n + tt(stage.n), data = pancreatic2, 
    tt = function(x, t, ...) x * log(t))

                coef exp(coef) se(coef)      z      p
stage.n       6.0096  407.3394   3.0598  1.964 0.0495
tt(stage.n)  -1.0858    0.3376   0.5889 -1.844 0.0652

Likelihood ratio test=6.33  on 2 df, p=0.04229
n= 41, number of events= 41

La función ajustada es

\[ \beta(t) \;=\; 6.01 \;-\; 1.09\,\log(t), \]

y el test de razón de verosimilitudes en conjunto (p=0.0423) ya detecta el efecto de estadío con efectos no proporcionales.

Podemos superponer esta forma teórica sobre un gráfico de residuos de Schoenfeld transformados:

resid.sch <- cox.zph(result.panc,
                     transform = function(time) log(time))
plot(resid.sch)                      # ejes en escala log
abline(coef(result.panc2.tt), col="red")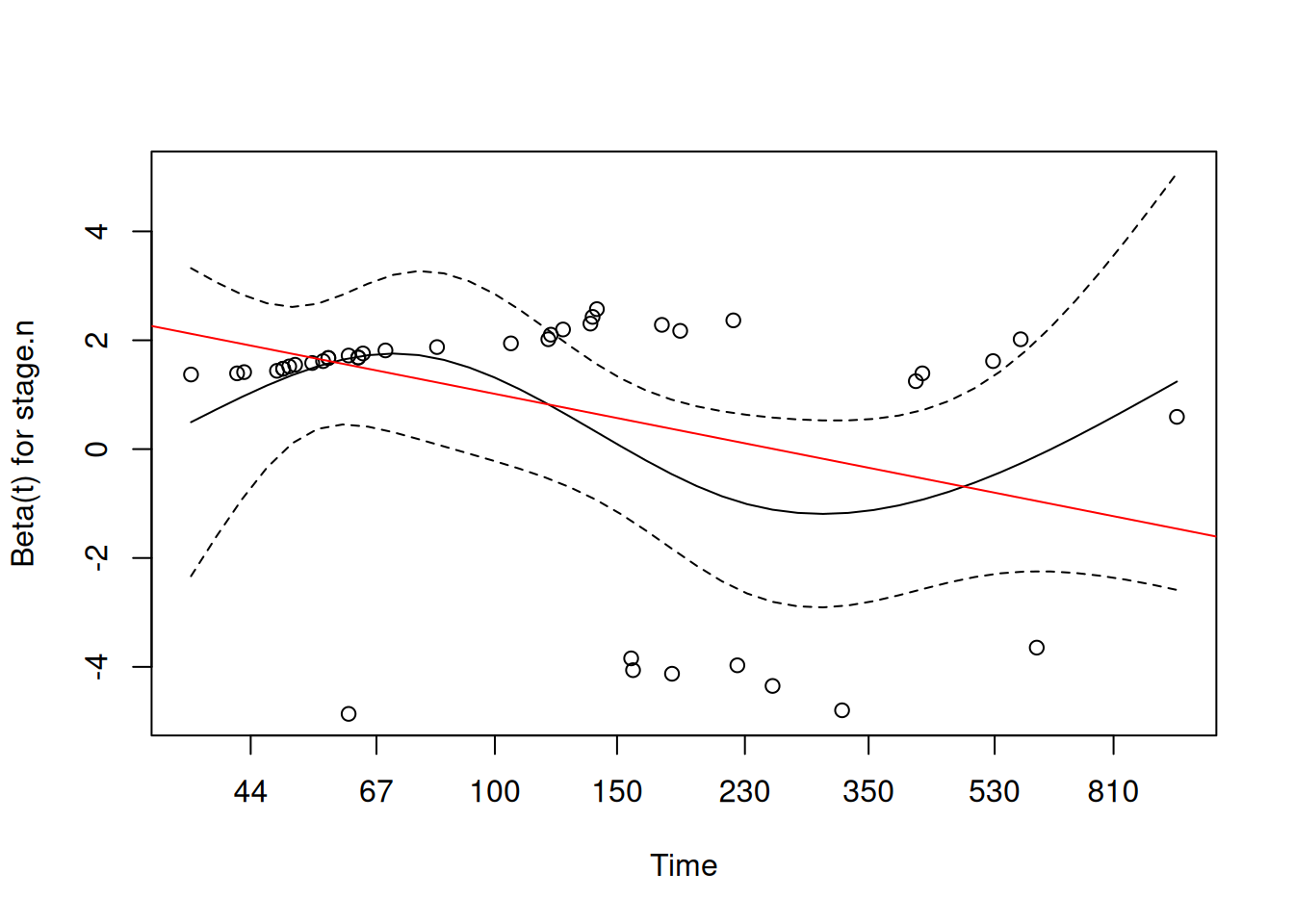

Para comparar, si usamos otra transferencia, por ejemplo \(g(t)=z\cdot t\), el término “tt(stage.n)” deja de ser significativo:

result.panc2.tt2 <- coxph(
  Surv(pfs) ~ stage.n + tt(stage.n),
  data = pancreatic2,
  tt = function(x, t, ...) x * t
)
result.panc2.tt2

Call:
coxph(formula = Surv(pfs) ~ stage.n + tt(stage.n), data = pancreatic2, 
    tt = function(x, t, ...) x * t)

                 coef exp(coef)  se(coef)      z      p
stage.n      1.278099  3.589808  0.661027  1.934 0.0532
tt(stage.n) -0.003656  0.996350  0.002532 -1.444 0.1487

Likelihood ratio test=4.56  on 2 df, p=0.1025
n= 41, number of events= 41

Este ejemplo ilustra que la elección de la función de transferencia de tiempo (i.e. de \(\beta(t)\)) es crucial para capturar correctamente el patrón de riesgos no proporcionales.

14.3.3.2 Variables Dependientes del Tiempo que Crecen Linealmente

Una duda frecuente es si podemos usar la edad del paciente como covariable dependiente del tiempo. Aunque el age at entry es fijo en \(t=0\), la edad real del paciente aumenta conforme avanza el tiempo de seguimiento. Para ilustrar por qué esto no aporta nueva información al modelo, usaremos el conjunto de datos lung del paquete survival, donde la edad está en años y el tiempo de supervivencia en días.

Primero, ajustamos un modelo de Cox simple con la edad al ingreso como covariable:

library(survival)

result1 <- coxph(Surv(time, status==2) ~ age, data=lung)
summary(result1)

Call:
coxph(formula = Surv(time, status == 2) ~ age, data = lung)

  n= 228, number of events= 165 

        coef exp(coef) se(coef)     z Pr(>|z|)  
age 0.018720  1.018897 0.009199 2.035   0.0419 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

    exp(coef) exp(-coef) lower .95 upper .95
age     1.019     0.9815     1.001     1.037

Concordance= 0.55  (se = 0.025 )
Likelihood ratio test= 4.24  on 1 df,   p=0.04
Wald test            = 4.14  on 1 df,   p=0.04
Score (logrank) test = 4.15  on 1 df,   p=0.04

El resultado muestra un efecto positivo de la edad inicial sobre el log-hazard (\(p=0.042\)).

Ahora redefinimos la edad como variable dependiente del tiempo, sumando al valor inicial el tiempo transcurrido (en años):

result2 <- coxph(
  Surv(time, status==2) ~ tt(age),
  data = lung,
  tt = function(x, t, ...) {
    age_current <- x + t/365.25
    age_current
  }
)
summary(result2)

Call:
coxph(formula = Surv(time, status == 2) ~ tt(age), data = lung, 
    tt = function(x, t, ...) {
        age_current <- x + t/365.25
        age_current
    })

  n= 228, number of events= 165 

            coef exp(coef) se(coef)     z Pr(>|z|)  
tt(age) 0.018720  1.018897 0.009199 2.035   0.0419 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

        exp(coef) exp(-coef) lower .95 upper .95
tt(age)     1.019     0.9815     1.001     1.037

Concordance= 0.55  (se = 0.026 )
Likelihood ratio test= 4.24  on 1 df,   p=0.04
Wald test            = 4.14  on 1 df,   p=0.04
Score (logrank) test = 4.15  on 1 df,   p=0.04

No hay ningún cambio en el ajuste ni en el valor \(p\). Matemáticamente, si denotamos

\[ z(0)=\text{edad al ingreso},\qquad z(t)=z(0)+t, \]

el hazard cobra la forma

\[ h(t)\;=\;h_0(t)\,e^{\beta\,z(t)} \;=\;\bigl[h_0(t)\,e^{\beta\,t}\bigr]\;e^{\beta\,z(0)}. \]

En la verosimilitud parcial el factor \(e^{\beta t}\) y el hazard base \(h_0(t)\) aparecen tanto en numerador como en denominador de cada término, y se cancelan. Solo queda el término \(e^{\beta,z(0)}\), de modo que \(\beta\) coincide exactamente con el obtenido usando la edad fija.

Este resultado se generaliza a cualquier covariable que aumente a ritmo constante con el tiempo (por ejemplo, exposición continua a un contaminante). Sin embargo, no ocurre si la covariable crece de forma no lineal; por ejemplo, usar

\[ g(t)=\log\bigl(z(0)+t\bigr) \]

rompe la cancelación y puede aportar nuevo efecto.